相关性分析(具体来说,皮尔逊成对相关性)和回归分析(具体来说,双变量最小二乘 (OLS) 回归)具有许多共同的特征:
- 两者都定期应用于两个连续变量(我们称之为 X 和 Y)。
- 通常向学生介绍这两种图表时使用的是同一类型的图表:散点图。
- 二者从根本上讲都是关于 X 中的偏差(即相对于平均值的单个值)与 Y 中的偏差之间的关系。
- 两者都假设 X 和 Y 之间存在线性关系。
- 两者都可以用于经典的假设检验,每个都依赖于相同的基础分布(t)并产生相同的p值。
事实上,双变量 OLS 回归中获得的流行 R 平方实际上就是皮尔逊相关系数 ( r ) 的平方。
那么相关性和双变量回归,有什么区别呢?
最大的区别在于我们如何解释每次分析产生的关键数量。我们从相关性分析中获得的相关系数 ( r ) 是一个标准化数字,介于 -1 到 +1 之间(其中 -1 表示完全负线性相关,而 +1 表示完全正线性相关),无论我们分析的变量是什么。
另一方面,回归会产生一个 beta 系数 ( b ),它可以是任意数字,告诉我们当 X 增加一个单位时 Y 的平均变化。换句话说,b是以我们正在研究的特定 Y 变量为单位的。因此,要真正理解b,我们确实需要知道 X 和 Y 是什么以及如何测量它们的细节
两者之间存在着更重要的概念差异
- ***r***是关于观测值围绕拟合线的聚集紧密程度,无论该线有多陡峭。
- *b*表示拟合线的陡峭程度,无论观测值围绕该线的聚集程度如何。
r实际上关心的是 X 的较高值往往(线性)与 Y 的较高值(或较低值)对应的一致性。而b实际上关心的是,在 X 增加的情况下,Y 预计平均会发生多大变化。
围绕斜线的观测值的聚集与斜线本身并不相同
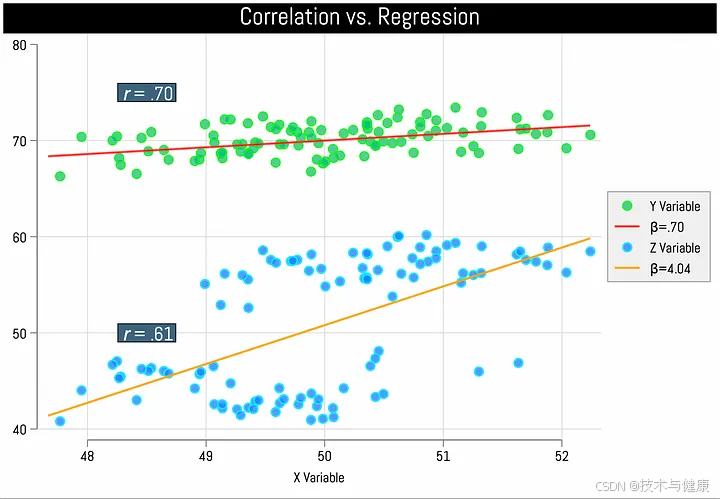
图表顶部的(绿色)点表示 X 和 Y 之间的关系。r值为0.70。此关系的 b 值也为 0.70。因此,存在相当强的正相关性,且“效应”为 0.70,这意味着当 X 增加 1 时,我们预计 Y(平均)将增加 0.70。此效应由穿过数据点的(红色)拟合线表示。
但现在看看下半部分的(蓝色)点。它们看起来相当混乱——它们看起来不像图表上半部分那样整齐地聚集在(橙色)拟合线周围。相对于上图,它们在拟合线周围分散得很开,这表明从 X 的一个值到 X 的较高值对应 Y 的较低值的情况相对较多*,*反之亦然。因此,我们的相关性(r)较低,现在只有 0.61,而上图为 0.70。
但现在请注意底部斜率的相对陡峭程度。平均而言,增加 X 的值会导致 Y 的预期值发生相当大的变化。因此,我们看到一个非常大的斜率: b =4.03。这意味着,X 每增加一个单位,我们平均会看到 Y 增加 4.03。这比我们在顶部看到的**b =.70 效应要陡峭得多,但底部的相关性 ( r ) 较弱。
再次强调,数据点在斜率周围的聚集程度与斜率本身并不是一回事。
举例: 现在是夏天,天气很热;你不喜欢你所在城市的高温,所以你决定去山上。幸运的是,你到达山顶,测量温度,你发现它比你所在城市的温度低。你会有点疑惑*(因为你对气温的下降不理解)*,于是决定去一座更高的山,发现那里的气温甚至比前一座山上的还要低。
你尝试不同高度的山脉,测量温度并绘制图表;你会发现,随着山的高度增加,温度降低,你可以看到一个线性趋势。这是什么意思?这意味着温度与高度有关;这并不意味着山的高度导致了温度的下降*(如果你用热气球到达同一高度、同一纬度,你会测量出什么温度?)*
相关性和回归分析不仅仅是对同一事物的不同表述方式。
补充
1.深入相关性这个概念,我们可以说,如果第一个变量的每一个值,都遵循一定的规律性对应于第二个变量的一个值,那么两个变量是相关的;因此,如果两个变量高度相关,路径将是线性的*(一条线)*,因为相关性描述了变量之间的线性关系。
也就是说,相关性表示的是变量之间的关系,而不是因果关系!如果自变量的值增加,而因变量的值也增加,但这并不意味着第一个变量导致了第二个变量值的增加!
2.回归分析是一种数学技术,用于分析一些数据,包括一个因变量和一个*(或多个)*自变量,目的是找到因变量和自变量之间的最终函数关系。
回归分析的目的是找到在因变量和自变量之间的一个估计值*(一个好的估计值!)*。从数学上讲,回归的目的是找到最适合数据的曲线。
当然,最适合数据的曲线可以是直线;但它也可以是任何曲线,这取决于它们之间是何种关系!
所以,我们要做的是计算相关系数,如果它的值接近1,我们可以在研究回归时得到一条直线;否则,我们必须尝试多项式回归*(或其他方法,比如指数回归或其他任何方法)*!