本篇会用到之前讲过的二叉树三种遍历方法的代码实现,当然这里还会再写一遍,可以先去看这篇博客二叉树的概念及三种遍历方法(C语言)_Perfectkn的博客-CSDN博客
目录
两种方法求二叉树结点总个数
简单递归调用
核心思想就是递归调用函数,第一种思路就是,定义一个变量,如果树不为空则让此变量+1,然后递归访问左子树和右子树,每一次访问到结点都让此变量+1。就是我们的代码实现过程。
另外,为了使每次我们调用的这个变量都能+1,所以此变量必须是全局变量,定义在函数外面,不然你想想,定义在函数里面,是不是每一次调用都会让其初始化成0或其他当时定义好的数。
下面就是代码实现。
int size = 0;
void TreeSize(BTNode* root)//求二叉树结点个数
{
if (root == NULL)
{
return;
}
else
{
++size;
}
TreeSize(root->left);
TreeSize(root->right);
}此时main函数是这样写。
int main()
{
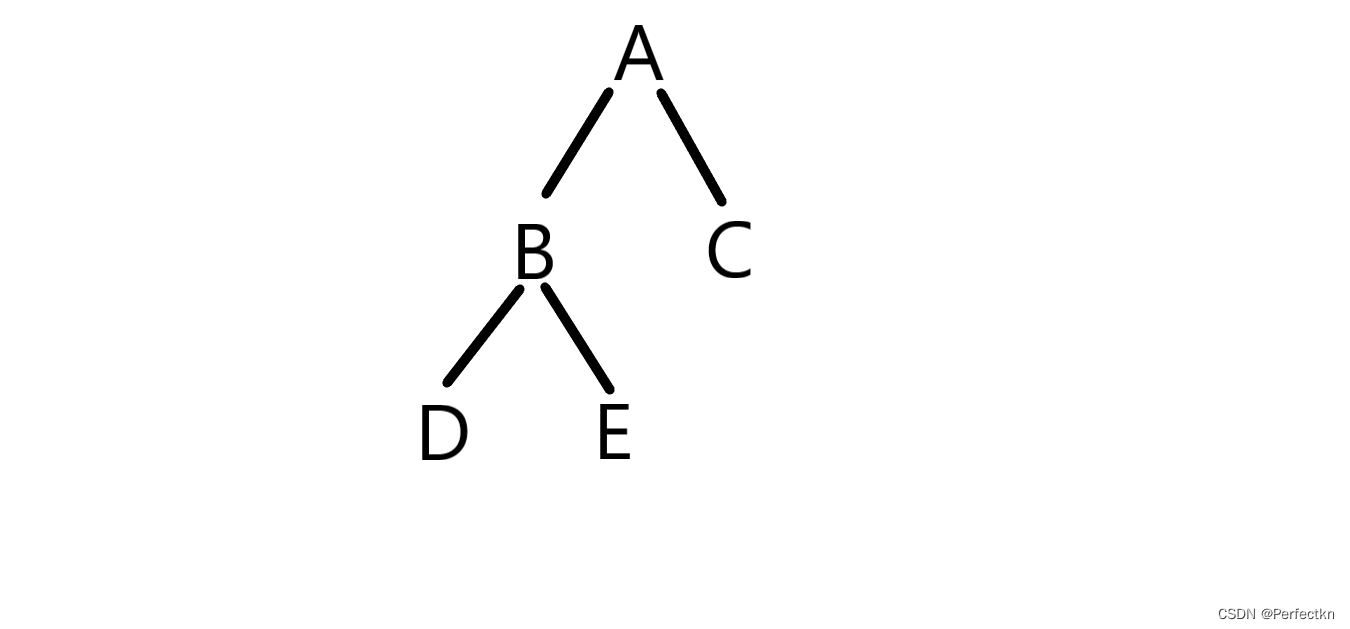
BTNode* A = (BTNode*)malloc(sizeof(BTNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTNode* B = (BTNode*)malloc(sizeof(BTNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTNode* C = (BTNode*)malloc(sizeof(BTNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTNode* D = (BTNode*)malloc(sizeof(BTNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTNode* E = (BTNode*)malloc(sizeof(BTNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
TreeSize(A);
printf("A TreeSize:%d\n", size);
size = 0;
TreeSize(B);
printf("B TreeSize:%d\n", size);
return 0;
} 注意事项:①不要忘记头文件#include<stdio.h> #include<stdlib.h>
②主函数调用求结点函数一次后,必须执行size = 0;这一步归零操作,不然接下来调用此函数时会出现size累加现象!
分治思想
分治思想就是:比如一个学校要求一下总人数,那么校长可以把几个年级主任叫过来,让他们去统计各年级的人数,然后年级主任回去又把本年级的班主任叫过来,让他们统计各班人数,最后相加,这就是分治思想。
以下是代码实现。
//分治的思想求二叉树结点数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}非常的简单粗暴一行了结。
讲解:先判断树是否为空,即root == NULL? 若为空则返回0,若不为空则返回TreeSize(root->left) + TreeSize(root->right) + 1。这样就会继续递归调用,最后加一就是加的根结点。
此时main函数调用就如下
printf("A TreeSize:%d\n", TreeSize(A));
printf("B TreeSize:%d\n", TreeSize(B));求叶子结点的个数
叶子结点就是度为0的结点。依然用分治思想。
如果树为空返回0,然后判断此结点是否是叶子结点的方法就是判断左子树右子树是否同时为空。最后递归调用访问其他不是叶子结点的结点。
以下是代码实现。
//求叶子结点的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}以上面的二叉树为例,从A开始判断是否是叶子结点。不是。执行return语句中TreeLeafSize(root->left) + TreeLeafSize(root->right)。
TreeLeafSize(root->left) 会访问到B结点,B也不是叶子结点,再执行return语句中TreeLeafSize(root->left) + TreeLeafSize(root->right)。
之后TreeLeafSize(root->left)会访问到D结点,D结点是叶子结点,return 1;
继续执行B结点处TreeLeafSize(root->right),访问到E结点,E结点是叶子结点,return 1;
此时B结点处收到的叶子结点总数为2,上报给A,A的左子树递归完毕,左子树叶子结点也求完了。
按此顺序继续递归即可,最好自己画一个图理解。