转自:https://www.jianshu.com/p/1d71ec4367d4
因为有需求,在知道一点经纬度和距离的情况下,需要知道另一点的经纬度。之前在网上也有查找,也有不少的案例,但是多数都是语焉不详,看不太明白。后来自己整理和重新再思考了下,这里给出一个自认为说得还算比较简明扼要的版本。
话不多说,具体如下:
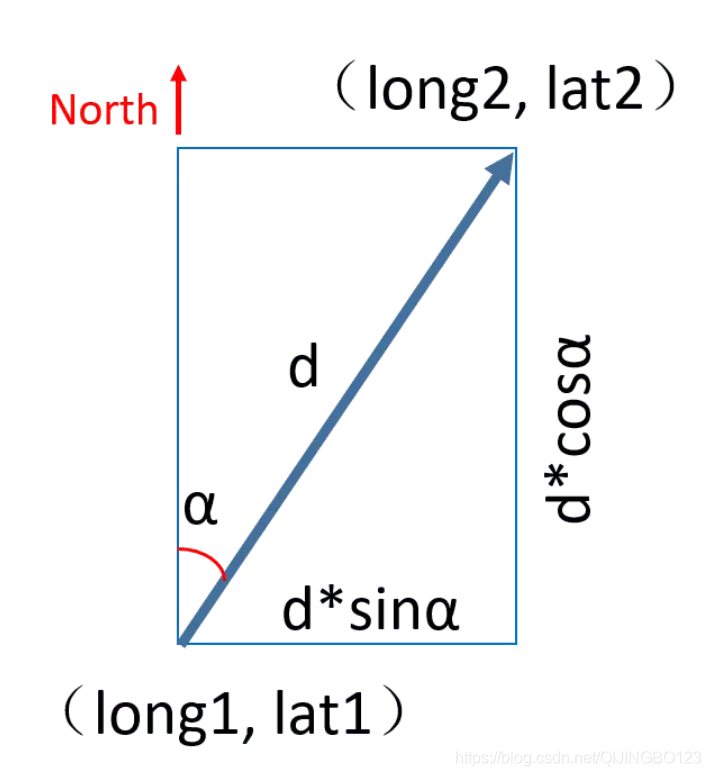
假设方位角是α, 那从点1到点2的平移距离分别如下所示dsinα, dcosα。 这里正北为0度。基中点1经纬度(long1, lat1)和距离d是已知的。 求点2的经纬度(long2,lat2)
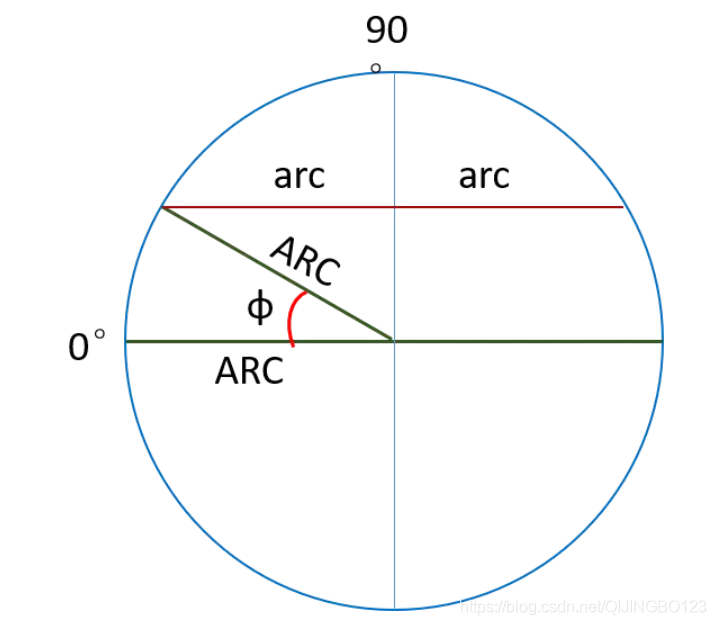
还有一个隐藏的信息,就是点1所在的纬度,其实也是一个有用的角度,通过它可以知道当前纬度的那个切面的半径长度,下图红线所示用arc表示。这里假设地球是近似球体,赤道圆的半径是ARC,侧从下图中可以得出:就是知道φ是当前点1的纬度。则当前的纬度的切面半径 arc = ARCcos(φ) ,其中φ其实就是当前的方位的纬度值,即arc = ARCcos(lat1)
这里还要再讨论下地球半径,其实地球是一个椭球体。
极半径 从地心到北极或南极的距离,大约3950英里(6356.9088千米)(两极的差极小,可以忽略)。
赤道半径 是从地心到赤道的距离,大约3963英里(6377.830千米)。如果只是做近似计算的,我们这里取平均距离,平均半径 大约3959英里(6371.393千米) 。这个数字是地心到地球表面所有各点距离的平均值。这里取平均半径那么ARC=6371.393*1000(米)通过上面的知识铺垫后, 计算就简单化了,
【计算思路】
- 计算第二点的经度,就是 水平平移的距度(dsinα)除以 当前纬度切面周长(2πarc),再每乘以360度) ,就知道了水平横向平移了多少度,再加上long1,就是long2的值了。
- 计算第二点的纬度,比较简单,就是, 垂直平移的距离d(dcosα)除以 地球纵向周长,再乘上360度,就知道纵向平移了多少度,再加上lat1,就知道lat2的值了。long2 = long1 + dsinα/[ARC*cos(lat1)2π/360] lat2 = lat1 +dcosα/ (ARC *2π/360)BTW, 最后再啰嗦一句,如果你是要通过编程实现的,一定要注意所用编程语言中,三角函数的值用的是度数还是弧度,不然也是得不到正确的结果的。