题目1: 前缀和
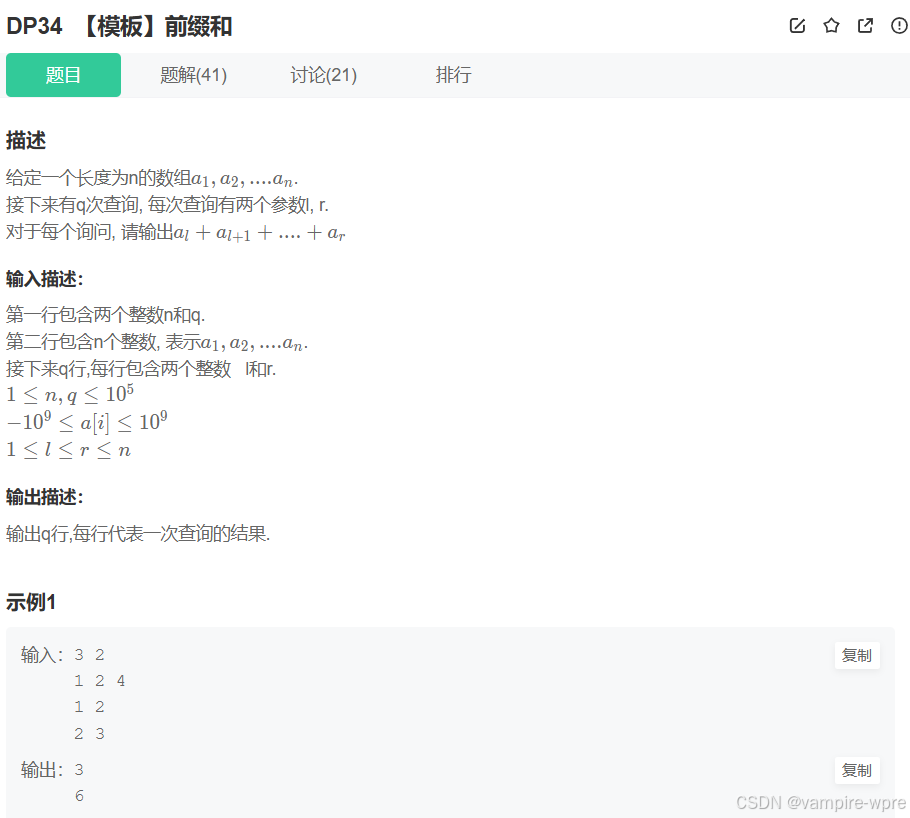
题目链接:【模板】前缀和_牛客网
解题思路:
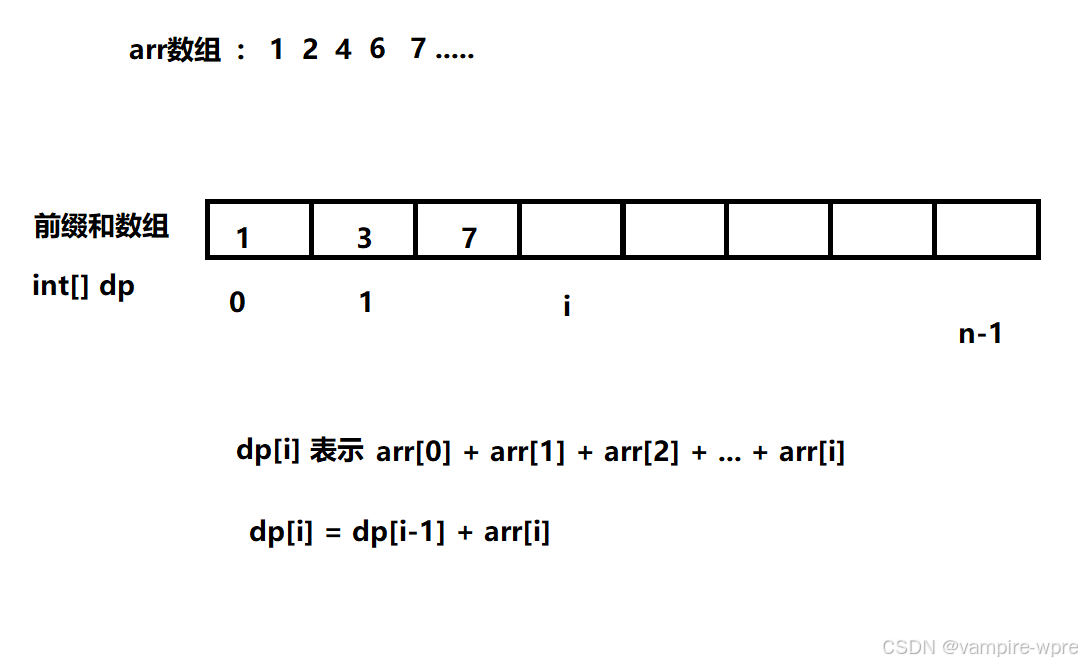
模拟出一个前缀和数组,如图,前缀和数组dp,dp[i]表示:arr[0]+arr[1]+arr[2]+…+arr[i]
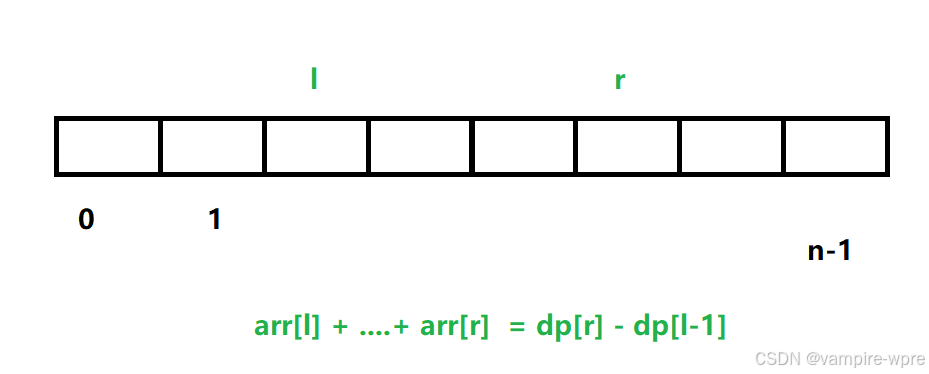
如何使用这个数组?根据题目要求,题目让我们求arr[l]+…+arr[r],而arr[l]+…+arr[r]就等于dp[r]-dp[l-1]
代码实现:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int q = in.nextInt();
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = in.nextInt();
}
long[] dp = new long[n + 1];
for (int i = 1; i <= n; i++) {
dp[i] = dp[i - 1] + arr[i];
}
while (q > 0) {
int l = in.nextInt();
int r = in.nextInt();
System.out.println(dp[r]-dp[l-1]);
q--;
}
}
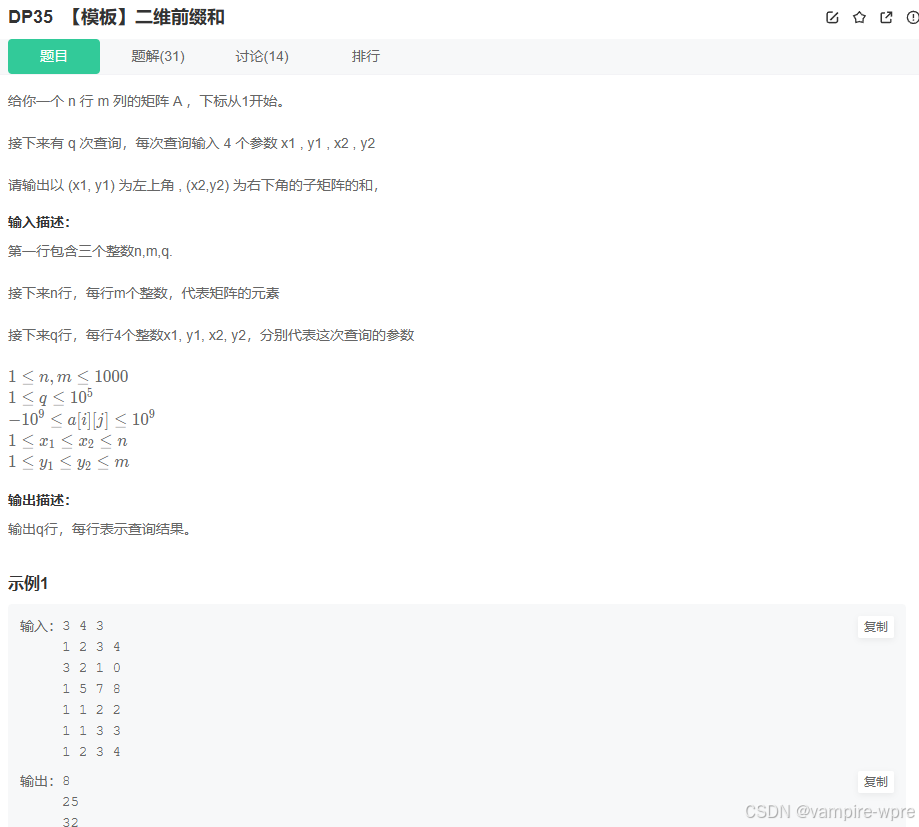
题目2: 二维前缀和
题目链接:【模板】二维前缀和 牛客网
解题思路:
思路和一维的前缀和数组类似,只不过这题是二维的数组,我们就称矩阵
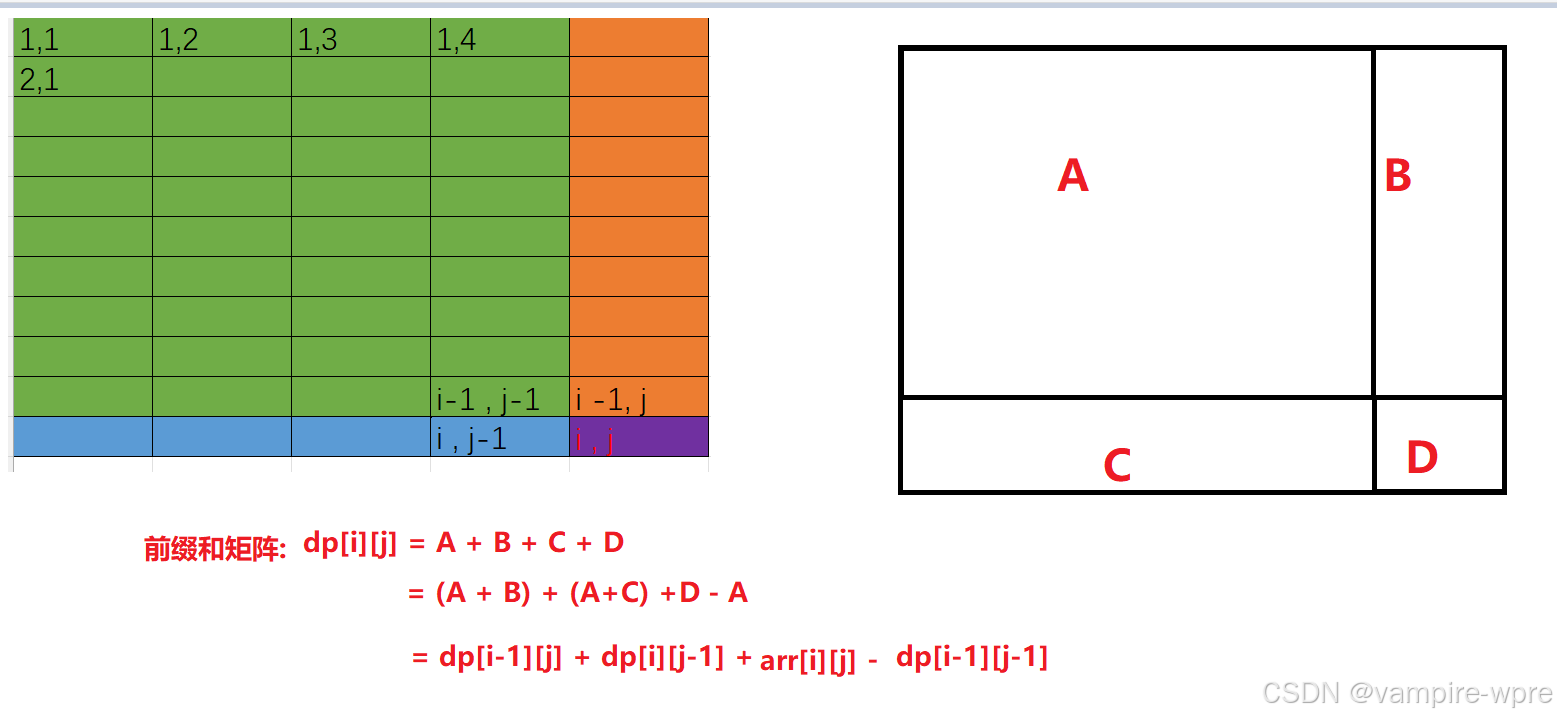
模拟出前缀和矩阵:
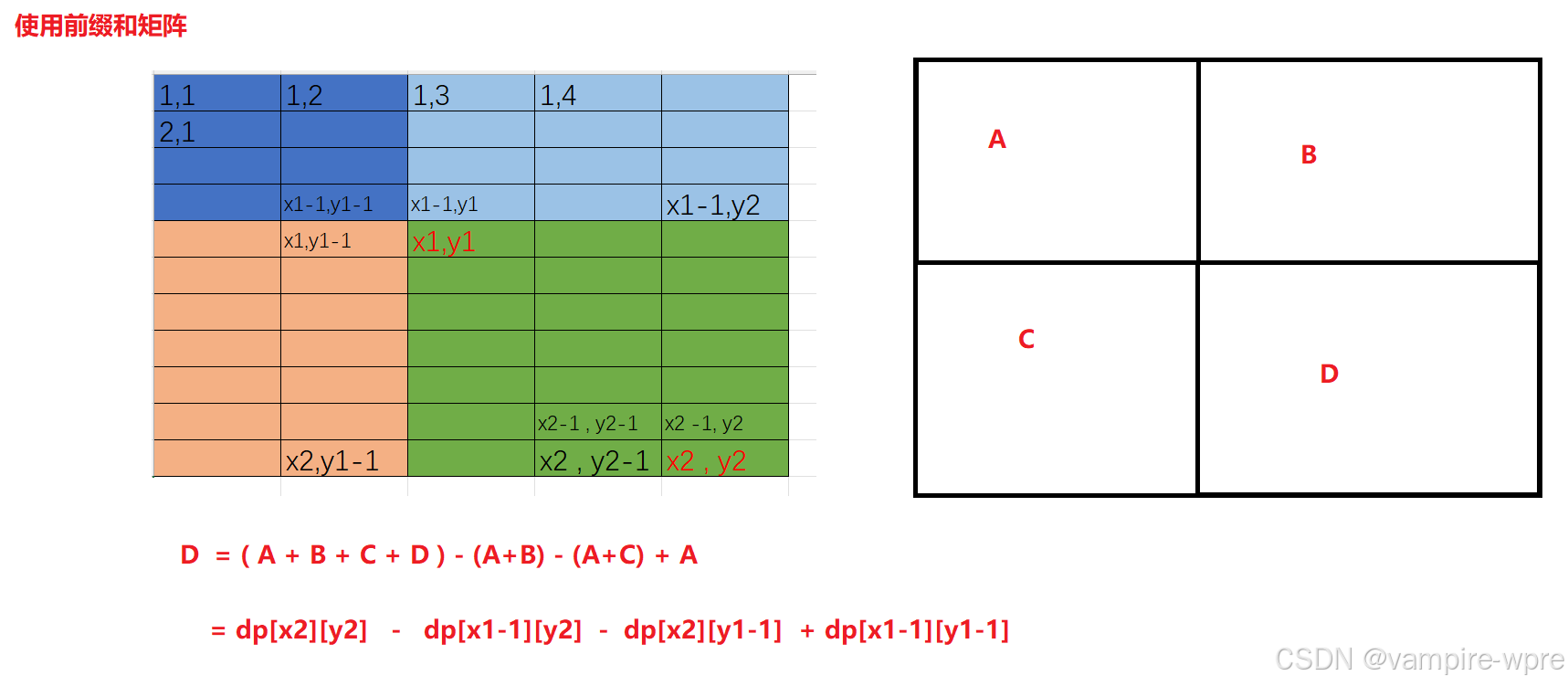
使用前缀和矩阵:
代码实现:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
int[][] arr = new int[n+1][m+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
arr[i][j]=in.nextInt();
}
}
long[][] dp = new long[n+1][m+1];
//前缀和矩阵
for(int i=1;i<=n;i++){
for(int j =1;j<=m;j++){
dp[i][j] = dp[i-1][j] +dp[i][j-1]+arr[i][j] - dp[i-1][j-1];
}
}
while(q>0){
int x1 = in.nextInt();
int y1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
System.out.println(dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]);
q--;
}
}
题目3: 寻找数组的中心下标
思路:创建一个前缀和数组跟一个后缀和数组
代码实现:
class Solution {
public int pivotIndex(int[] nums) {
int n = nums.length;
int[] f = new int[n];// 前缀和数组
int[] g = new int[n];// 后缀和数组
// 数组预处理
f[0] = 0;
g[n - 1] = 0;
//往前缀和数组前数据
for(int i=1;i<n;i++) {
f[i] = f[i-1] +nums[i-1];
}
//往后缀和数组前数据
for(int i=n-2;i>=0;i--) {
g[i]=g[i+1]+nums[i+1];
}
//使用前缀和数组、后缀和数组
for(int i=0;i<n;i++) {
if(f[i]==g[i]) {
return i;
}
}
return -1;
}
}
题目4: 除自身以外数组的乘积
题目链接:238. 除自身以外数组的乘积 - 力扣(LeetCode)
思路:其实这题和上一题中心下标的题是类似的,只不过把和变成积,我们要创建一个前缀积数组跟一个后缀积数组
代码实现:
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] ret = new int[n];
int[] f = new int[n];//前缀积数组
int[] g = new int[n];//后缀积数组
f[0] = 1;
g[n-1] = 1;
for(int i=1;i<n;i++) {
f[i] = f[i-1] * nums[i-1];
}
for(int i=n-2;i>=0;i--) {
g[i] = g[i+1] * nums[i+1];
}
//填数组
for(int i=0;i<n;i++) {
ret[i] = f[i] * g[i];
}
return ret;
}
}
题目5: 和为K的子数组
题目链接:560. 和为 K 的子数组 - 力扣(LeetCode)
枚举所有的子数组的方法: 以前我们一般使用的是从前往后枚举,就是两个for循环,从i位置开始往后进行枚举,其实我们也可以从i位置往前进行枚举,这两个方法都能枚举出全部的子数组。
思路:
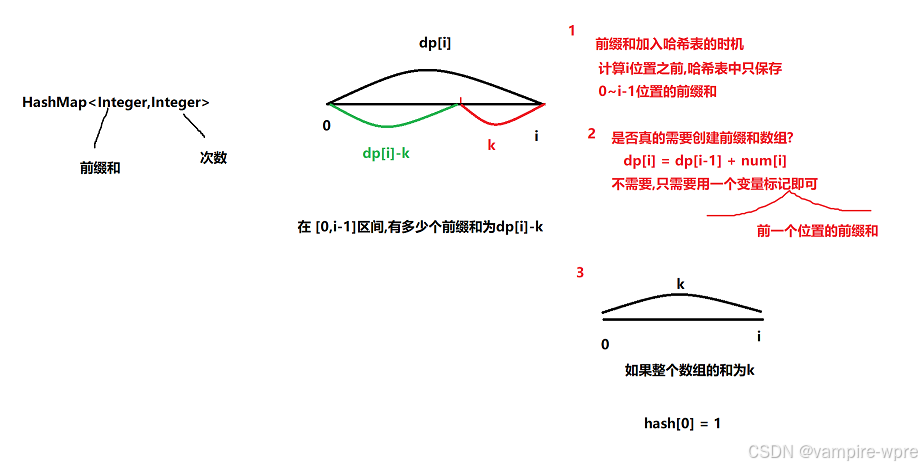
因为我们采用的是从后往前枚举子数组,所以我们可以把问题转换为:求在[0,i-1]区间内,有多少个前缀和为dp[i] - k,dp[i] 就是i位置的前缀和
代码实现:
class Solution {
public int subarraySum(int[] nums, int k) {
HashMap<Integer, Integer> hash = new HashMap<>();
hash.put(0, 1);
int dp = 0;
int ret = 0;
for (int i = 0; i < nums.length; i++) {
dp += nums[i];// 计算当前位置的前缀和
ret += hash.getOrDefault(dp - k, 0);// 统计结果的个数
hash.put(dp, hash.getOrDefault(dp, 0) + 1);//计算之后丢进哈希表中
}
return ret;
}
}
题目6: 和可被k整除的子数组
974. 和可被 K 整除的子数组 - 力扣(LeetCode)
补充知识:
1、同余定理
(a-b)/ p = k…0 ==> a%p = b%p
2、负数%正数的结果以及修正
负数%正数的结果是一个负数
修正: a%p ==>(a%p + p)%p
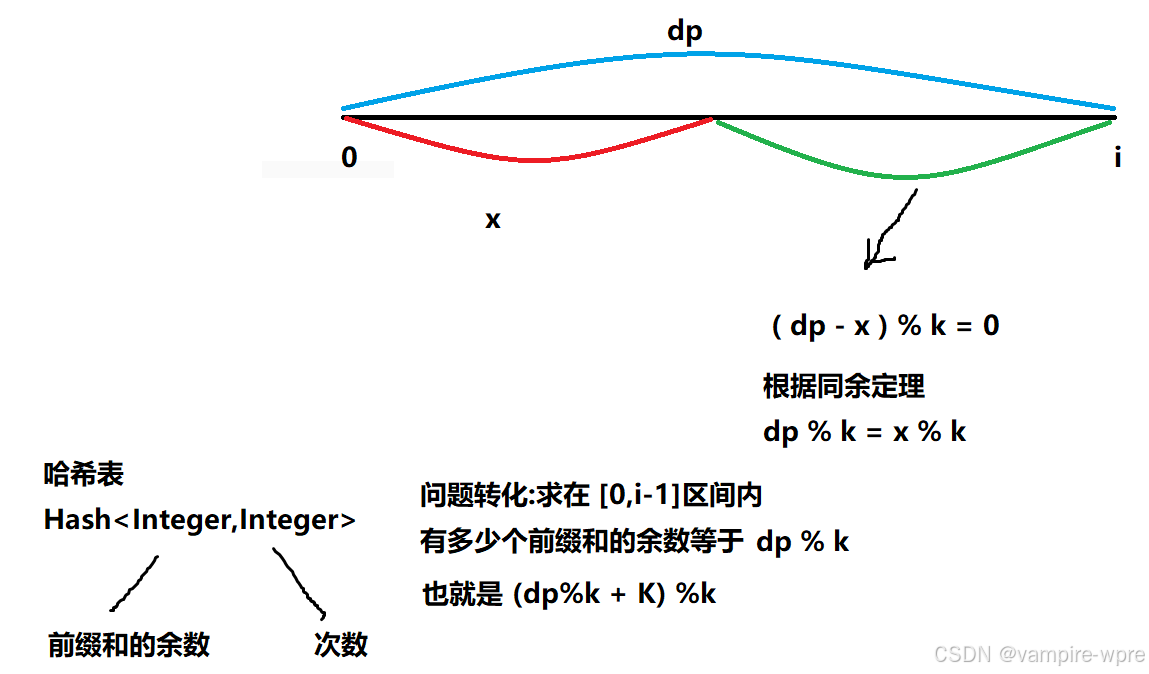
思路:
代码实现:
class Solution {
public int subarraysDivByK(int[] nums, int k) {
HashMap<Integer, Integer> hash = new HashMap<>();// 前缀和的余数,次数
hash.put(0 % k, 1);
int dp = 0;
int ret = 0;
for (int i = 0; i < nums.length; i++) {
dp += nums[i];//计算当前位置的前缀和
ret += hash.getOrDefault((dp % k + k) % k, 0);//统计结果
//把余数丢进哈希表中
hash.put((dp % k + k) % k, hash.getOrDefault((dp % k + k) % k, 0) + 1);
}
return ret;
}
}
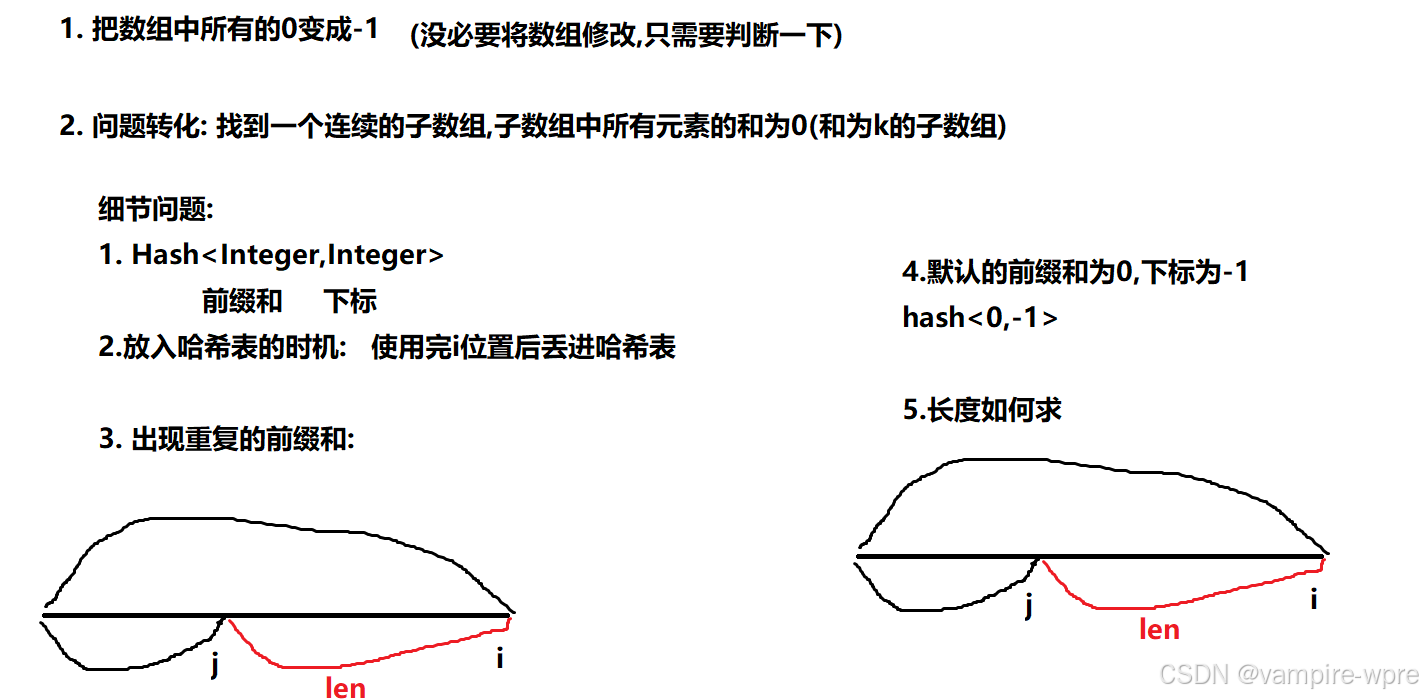
题目7: 连续数组
思路:
代码实现:
class Solution {
public int findMaxLength(int[] nums) {
HashMap<Integer, Integer> hash = new HashMap<>();// 前缀和
hash.put(0, -1);
int dp = 0, len = 0;
for (int i = 0; i < nums.length; i++) {
dp += (nums[i] == 0 ? -1 : 1);// 计算位置当前前缀和
if (hash.containsKey(dp)) {
len = Math.max(len, i- hash.get(dp));
} else {
//如果不存在则加入哈希表
hash.put(dp, i);
}
}
return len;
}
}
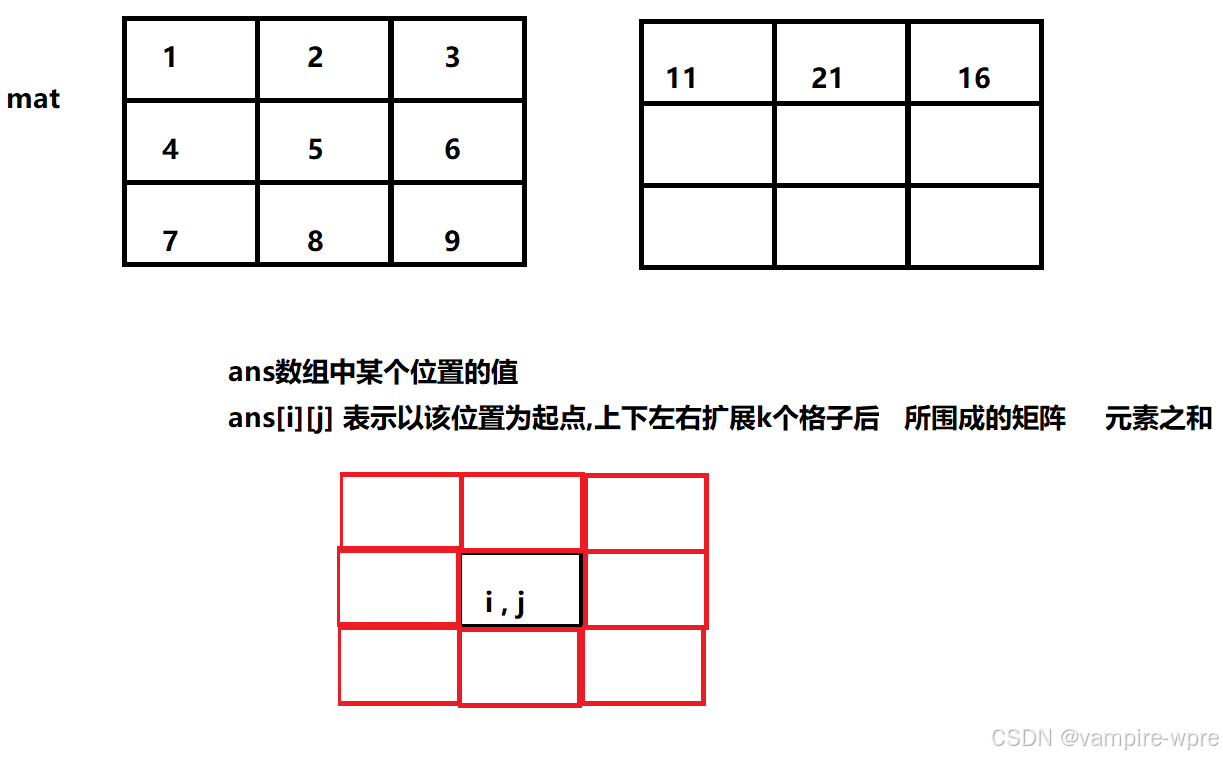
题目8: 矩阵区域和
题目解析:
解题思路:
利用二维前缀和,求前缀和的计算方法和本系列第二题一样
代码实现:
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int m = mat.length;
int n = mat[0].length;
// 前缀和矩阵
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
// 使用矩阵
int[][] ret = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
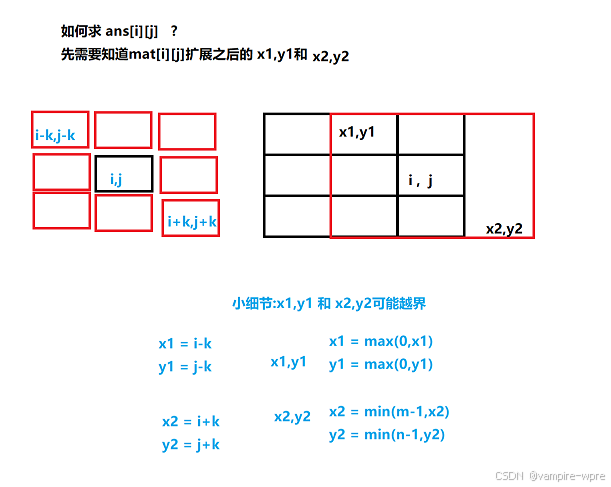
int x1 = Math.max(0, i - k) + 1;
int y1 = Math.max(0, j - k) + 1;
int x2 = Math.min(m - 1, i + k) + 1;
int y2 = Math.min(n - 1, j + k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
}
}
return ret;
}
}