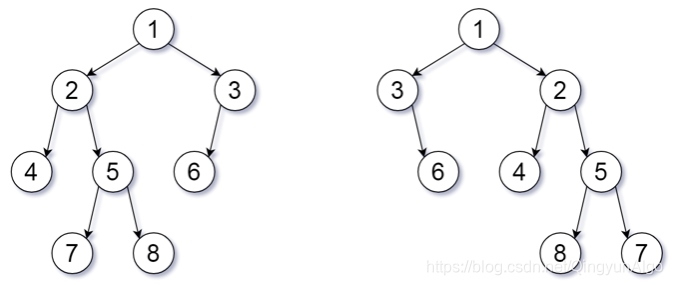
题目:在二叉树中选中一个节点并交换它的左右子树,称之为一个翻转操作。如果一棵二叉树X经过若干次翻转操作之后能够变成二叉树Y,那么二叉树X和Y是翻转等价的。请判断两棵二叉树是不是翻转等价。假设二叉树节点的值唯一。例如,我们翻转下图中左边二叉树节点1、3、5的左右子树,就得到了右边的二叉树,因此它们是翻转等价的。
分析:这是LeetCode第951题。
按照题目中翻转等价的定义,如果两棵二叉树翻转等价,那么首先它们的根节点要相同。如果根节点不同,那么两棵二叉树一定不是翻转等价。
接下来看左右子树是否翻转等价。这里要分两种情况讨论。第一种可能是不用交换根节点的左右子树,此时分别判断第一棵树的左子树和第二棵树的左子树是否翻转等价,以及第一棵树的右子树和第二棵树的右子树是否翻转等价。第二种可能是需要交换根节点的左右子树,此时分别判断第一棵树的左子树和第二棵树的右子树是否翻转等价,以及第一棵树的右子树和第二棵树的左子树是否翻转等价。
怎么判断子树翻转等价?这和判断整棵树翻转等价是同一个问题,可以递归解决。参考代码如下:
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null) {
return true;
}
if (root1 == null || root2 == null || root1.val != root2.val) {
return false;
}
return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right))
|| (flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
}
由于需要遍历整棵树,因此时间复杂度是O(n),n为二叉树中节点的数目。
更多算法面试题的讨论,欢迎访问博客http://qingyun.io/blogs。