今天我们来聊聊递归喝汽水问题

君子食无求饱，居无求安，敏于事而慎于言，就有道而正焉，可谓好学也已

递归直通车

再识帝龟
面试题警告
最后

再识帝龟

大家好，我是帝龟，好久不见！！！
在这里插入图片描述
关于我的基本介绍，大家可以到以下链接中找寻我的身影：

面试题警告

可能是由于本帝龟平时非常喜欢喝汽水，所以面试官似乎经常喜欢用喝汽水的问题当做面试题来考考大家对于本帝龟的熟悉程度。如这是我朋友最近几天碰到的面试题：

1元钱一瓶汽水，喝完之后两个空瓶换一瓶汽水。问：若你有N元钱，你最多能喝多少瓶汽水?

又或者说，我们来看一道华为的面试题：

一个人买汽水，一块钱一瓶汽水，三个瓶盖可以换一瓶汽水，两个空瓶可以换一瓶汽水，问20块钱可以买多少汽水？

题1解

我们先来看题1：

1元钱一瓶汽水，喝完之后两个空瓶换一瓶汽水。问：若你有N元钱，你最多能喝多少瓶汽水?

看到这个题目，可能大家觉得非常简单，然后就飞快的在草稿纸上计算了起来：

钱数（元） - 	   瓶数
  1            	1
  2            	3=2+1
  3            	5=3+1+1
  4            	7=4+2+1
  ...			...
  n			    2n-1

经过以上分析，无论是通过列出一元一次方程还是通过观察得出这是一个首项为1，公差为2的等差数列，都可以轻而易举地得出：当你有N元钱时，如果你不怕撑的话，最多能喝2N-1瓶汽水。

但是如果让你用代码解，你会怎么解呢？

我们试着来分析一下这个题目（暂时先不考虑换不完问题)：
首先我有N元钱，买了N瓶汽水，喝完汽水剩下N个空瓶；
然后用N个空瓶，换了N/2瓶汽水，喝完汽水剩下N/2个空瓶；
然后用N/2个空瓶，换了(N/2)/2瓶汽水，喝完汽水剩下(N/2)/2个空瓶；
…
最后用2个空瓶，换了一瓶汽水，喝完汽水剩下一个空瓶（换不了，扔掉）

这样试着一分析，这似乎是一个循环往复，周而复始的问题：拿到汽水，再用空瓶换汽水。而且当只有一瓶汽水的时候兑换结束，这不就是一个中止条件吗？好的，分析完毕，我们可以刷刷刷写下以下代码：

/**
     * 计算最多能喝多少瓶汽水，并返回这个值
     * @param n 表示有n瓶汽水
     * @return
     */
    private static int soda(int n) {

        if (n == 1) {
            // 递归终止条件，当还有一瓶饮料的时候只能喝一瓶,不能再换了
            return 1;
        }else if(n % 2 == 0) {
            // 偶数瓶，这时空瓶刚好能够换完
            return n + soda(n/2);
        }else {
            // 奇数瓶，这一次剩下的一个空瓶子刚好和最后一次的一个空瓶子能换一瓶饮料，所以要+1
            return n + 1 + soda(n/2);
        }
    }

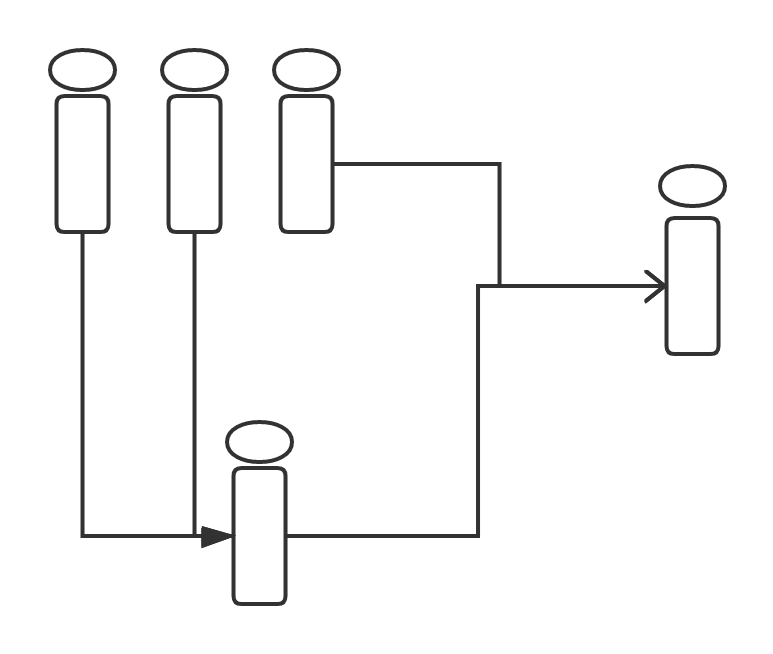
至于为什么奇数瓶时要+1，我们可以试着画一下当有3瓶饮料时的兑换图：
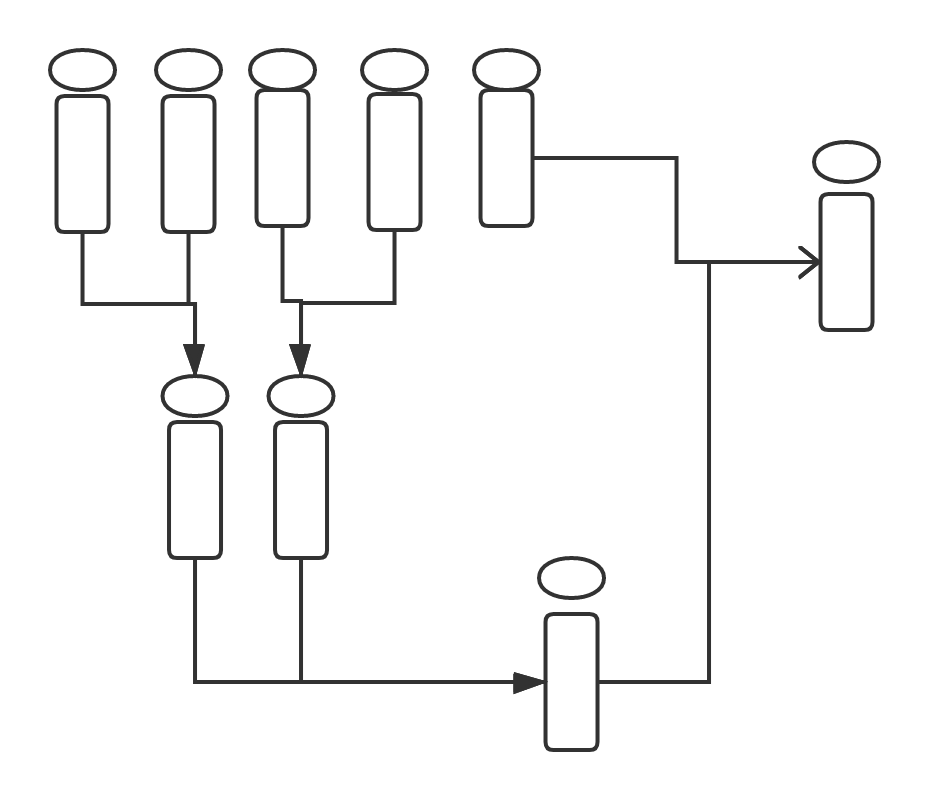
在这里插入图片描述
要是还是无法理解的话，我们再试着画一下当有5瓶饮料时的兑换图：

这样就可以发现当有奇数瓶时再复杂的情况无非也就是3瓶时的叠加。
我们再试着在main方法里面调用一下，来检验一下结果：

public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        for(;;) {
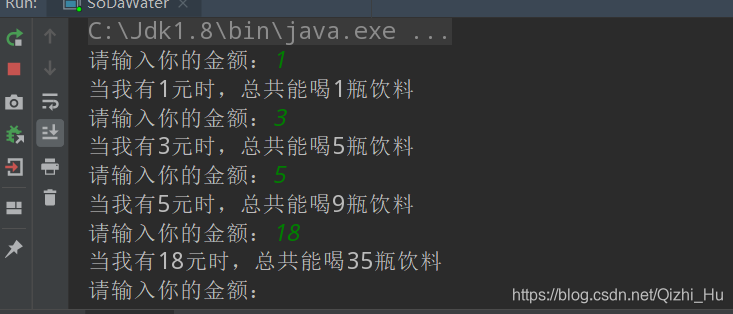
            System.out.print("请输入你的金额：");
            //从键盘输入我的钱数
            int money = scanner.nextInt();
            // 第一次的钱能喝的汽水瓶数(一元钱一瓶汽水)
            int n = money / 1;
            // 我能喝的汽水数
            int sum = soda(n);
            System.out.println("当我有" + money + "元时，总共能喝" + sum + "瓶饮料");
        }
    }

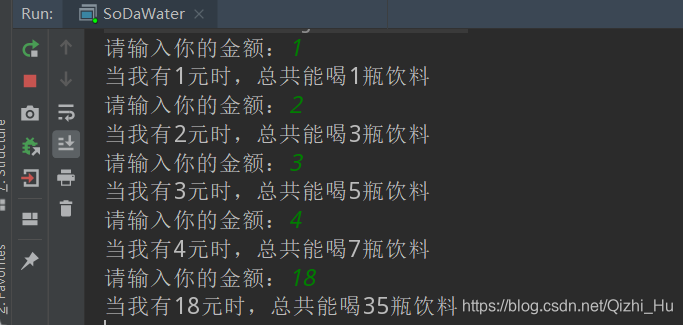
运行main方法，控制台结果如下：
在这里插入图片描述
简直完美！！！当然之前在我的这篇博客： - 递归和循环之间不得不说的故事中就提到过，递归能解决的问题循环一般也能解决，如：

	/**
     * 用循环来计算最多能喝多少瓶汽水
     * @param n
     * @return
     */
    private static int soda2(int n) {

        // 总共能喝的饮料瓶数
        int sum = n;

        // 当n==1时循环结束，所以n>1
        for (; n > 1; n = n/2) {
            if (n % 2 == 0) {
                sum += n/2;
            }else {
                // 此次的饮料瓶数是奇数瓶就补1
                sum += (n/2 + 1);
            }
        }
        
        return sum;
    }

我们将上面main方法中计算喝汽水的方法改为这个方法：

// 我能喝的汽水数
int sum = soda2(n);

运行main方法，从控制台得到结果如下：
在这里插入图片描述
结果是一样的。不过我突然想到，既然之前一开始已经推导出了：当你有N元钱时，如果你不怕撑的话，最多能喝2N-1瓶汽水。 那我还这么麻烦干甚？

所以我们可以很轻松的写出第三种方法：

	/**
     * 直接用推导出的数学公式计算
     * @param n
     * @return
     */
    private static int soda3(int n) {
        return 2 * n - 1;
    }

再调用测试一下：

// 我能喝的汽水数
int sum = soda3(n);

运行main方法：
在这里插入图片描述
如此简单的代码，结果竟然是一模一样的，让我叹服。数学不愧是一切科学的基础，被誉为科学的皇后。以后要是让我看见数学好的大哥：

大招

经过上述的分析，在考虑到本博主数学不好不能保证：每次遇到问题都能推导出数学公式的前提下，有这样两个问题：

奇数瓶时的+1不太好理解，导致代码可读性较差
作为本文主角的递归似乎显得有些弱鸡，和循环的解法相比似乎没有什么两样，而且递归的空间复杂度要更高（~~又要入栈，又要出栈的能不高吗？~~ ）

难道递归真的如此弱鸡吗？这个时候，我突然想起了某位名人说过的话：

To Iterate is Human, to Recurse, Divine.(人理解迭代，神理解递归)

窃以为，递归的一大优势就在于描述：能够用简单、有限的语句，描述出复杂、庞大的问题。而后采用分而治之的思想，将一个大问题拆解成一个个元问题并加以解决。好了，我要放大招了！

我们再试着回顾一下之前对于这个喝汽水问题的分析:

首先我有N元钱，买了N瓶汽水，喝完汽水剩下N个空瓶；
然后用N个空瓶，换了N/2瓶汽水，喝完汽水剩下N/2个空瓶；
然后用N/2个空瓶，换了(N/2)/2瓶汽水，喝完汽水剩下(N/2)/2个空瓶；
…
然后用2个空瓶，换了一瓶汽水；
最后喝完汽水剩下一个空瓶（换不了，扔掉）

有什么新的发现吗？

是的，我们可以发现在每次周而复始的过程中：不但有汽水这个变量，还有空瓶这个变量。 我们试着引入空瓶这个变量，刷刷刷：

	/**
     * 用递归计算出最多能喝多少瓶汽水
     * @param n 饮料瓶数
     * @param bottle 空瓶数
     * @return
     */
    private static int soda1(int n, int bottle) {

        // 兑换剩下的空瓶数
        bottle %= 2;
        // 喝完饮料剩下的空瓶数
        bottle += n;

        if (bottle < 2) { // 如果空瓶数<2，停止兑换
            return n;
        } else {
            return n + soda1(bottle/2, bottle);
        }
    }

试着来调用测试一下：

// 我能喝的汽水数
int sum = soda1(n, 0);

运行main方法：
在这里插入图片描述
这下才是真的完美，代码可读性也比之前要强很多了。而如果要用循环来控制两个变量来解决这个问题的话，那么代码很可能又会变得非常复杂。

题2解

看到这里，大家可能已经忘了题目二是啥了。不过莫得事，我们先来回顾一下题二：

一个人买汽水，一块钱一瓶汽水，三个瓶盖可以换一瓶汽水，两个空瓶可以换一瓶汽水，问20块钱可以买多少汽水？

我们可以先试着像题1一样在草稿纸上计算一下，看看能不能找到规律：

钱数（元） - 	   瓶数
  1            	1
  2            	5 = 2 + 1(2个空瓶) + 1(3个瓶盖) + 1(2个空瓶)
  3            	? = 3 + 1(2个空瓶) + 1(3个瓶盖) + ？？？
  ...			...
  20		    ？？？
  ...			...
  n			    ？？？

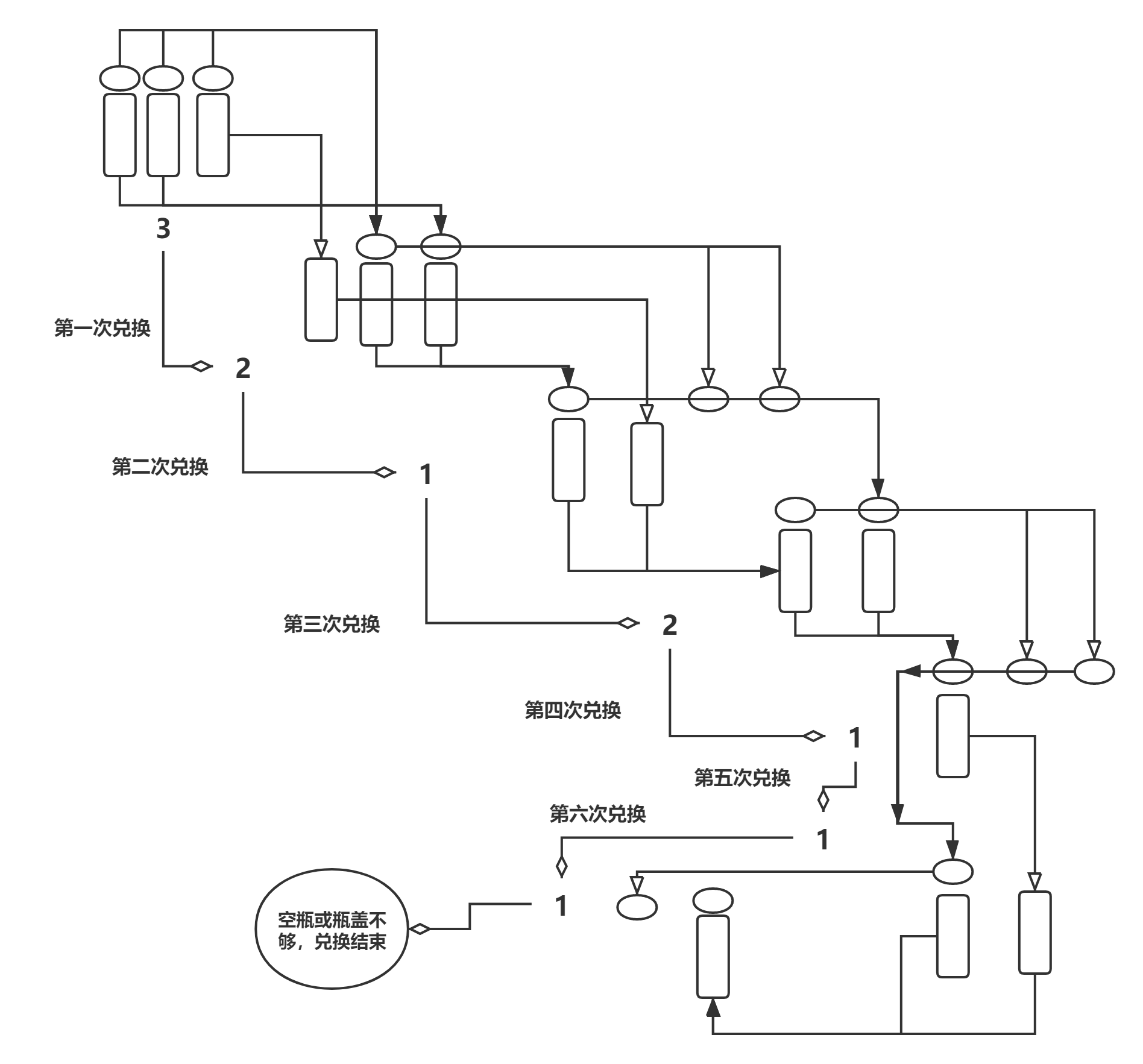
好吧，这个问题确实有点复杂，我计算到3块钱的时候就已经吃不消了，不愧是华为大佬们出的面试题。但是我不能服输，3块钱的最多喝饮料瓶数我就算跪着画图我也要强行算完。如下图，我们用空白的三角箭头(▷)表示上次兑换剩下来的瓶盖或者瓶子，用全黑的三角箭头(▶)表示兑换成功的饮料：
在这里插入图片描述

通过上图，我们可以很轻松的计算出3块钱的时候最多喝的饮料数为：3+2+1+2+1+1+1=11(瓶)。

~~确实很轻松~~ 哇，这也太难了吧。这个时候我们无论是用循环，还是说利用数学推导出数学公式(可能是我数学太菜)来计算出这个问题都很难。不过，本文的主角递归这下可就派上大用场了。有了之前的题1的讲解，相信大家理解以下代码就会变得很容易：

import java.util.Scanner;

/**
 * @author guqueyue
 * @Date 2020/6/25
 * 一个人买汽水，一块钱一瓶汽水，三个瓶盖可以换一瓶汽水，两个空瓶可以换一瓶汽水
 * 问20块钱可以买多少汽水？
 **/
public class SoDaWater2 {
    public static void main(String[] args) {

        Scanner scanner = new Scanner(System.in);

        for(;;) {
            System.out.print("请输入你的金额：");
            //从键盘输入我的钱数
            int money = scanner.nextInt();
            // 第一次的钱能喝的汽水瓶数(一元钱一瓶汽水)
            int n = money / 1;
            // 我能喝的汽水数
            int sum = sodaWater(n, 0, 0);
            System.out.println("当我有" + money + "元时，总共能喝" + sum + "瓶饮料");
        }
    }

    /**
     * 用递归计算n元钱最多能喝多少瓶汽水
     * @param n 饮料瓶数
     * @param bottle 空瓶数
     * @param cap 瓶盖数
     * @return
     */
    private static int sodaWater(int n, int bottle, int cap) {

        // 兑换剩下的空瓶数
        bottle %= 2;
        // 喝完饮料剩下的空瓶
        bottle += n;

        // 兑换剩下的瓶盖数
        cap %= 3;
        // 喝完饮料剩下的瓶盖
        cap += n;

        if (bottle < 2 && cap < 3) { // 如果空瓶数<2 并且 瓶盖数<3, 那么停止兑换
            return n;
        }else {
            return n + sodaWater(bottle/2 + cap/3, bottle, cap);
        }
    }

}

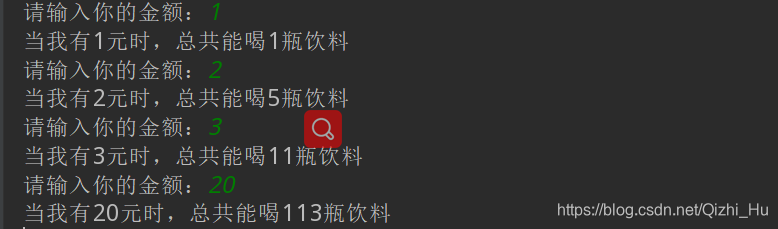
运行main方法，测试一下：
在这里插入图片描述
我们可以得出：当有20块钱，如果我不怕撑的话，我最多能喝113瓶饮料。

最后

如果你看到这里的话，希望我的这篇博客能够给你带来启发或者帮助。
我的完美主义拖延症导致了我的这篇博客从端午前写到了端午后。今天已经是端午节假期的第二天了，就不祝大家端午安康，祝大家端午假期快乐，没有bug！
在这里插入图片描述

创作不易，非常欢迎大家的点赞、评论和关注(^_−)☆
你的点赞、评论以及关注是对我最大的支持和鼓励，而你的支持和鼓励是我继续创作高质量博客的动力！！！