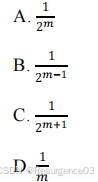渐进分析

【2010-THU-Mid】f(n) = O(g(n))，当且仅当g(n) = Ω(f(n))。（√）

【2010-THU-Mid】若f(n) = O(n^2)且g(n) = O(n)，则以下结论正确的是（AD）
A. f(n) + g(n) = O(n^2)

B. f(n) / g(n) = O(n)

C. g(n) = O(f(n))

D. f(n) * g(n) = O(n^3)

考虑f(n) = 1，g(n) = 1/n，BC错

【2010-THU-Mid】算法g(n)的复杂度为Θ(n)。若算法f(n)中有 5 条调用g(n)的指令，则f(n)的复杂度为（D）
A. Θ(n)

B. O(n)

C. Ω(n)

D. 不确定

【2010-THU-Mid】给出函数F(n)复杂度的紧界（假定int字长无限，移位属基本操作，且递归不会溢出）

void F(int n)           //O(        )
{ for(int i = 0, j = 0; i < n; i += j, j++); }
/*---------------------------------------------------------------------*/
void F(int n)           //O(        )
{ for (int i = 1; i < n; i = 1 << i); }
/*---------------------------------------------------------------------*/
int F(int n)           //O(        )
{ return (n < 4) ? n : F(n >> 1) + F(n >> 2); }
/*---------------------------------------------------------------------*/
int F(int n)           //O(        )
{ return (n == 0) ? 1 : G(2, F(n ‐ 1)); }
/*---------------------------------------------------------------------*/
int G(int n, int m)
{ return (m == 0) ? 0 : n + G(n, m ‐ 1); }
/*---------------------------------------------------------------------*/
int F(int n)           //O(        )
{ return G(G(n ‐ 1)); }
/*---------------------------------------------------------------------*/
int G(int n)
{ return (n == 0) ? 0 : G(n ‐ 1) + 2 * n ‐ 1; }
/*---------------------------------------------------------------------*/
void F(int n) {         //O(        )
    for (int i = 1; i < n; i++)
        for (int j = 0; j < n; j += i);
}
/*---------------------------------------------------------------------*/
void F(int n) {     //expected‐O(        )
   for (int i = n; 0 < i; i‐‐)
      if (0 == rand() % i)
         for (int j = 0; j < n; j++);
}

向量

【2010-THU-Mid】对有序向量做Fibonacci查找，就最坏情况而言，成功查找所需的比较次数与失败查找相等。（√）

【2010-THU-Mid】对于同一有序向量，每次折半查找绝不会慢于顺序查找。（×）

【2010-THU-Mid】现有长度为 15 的有序向量A[0..14]，各元素被成功查找的概率如下：

若采用二分查找算法，试计算该结构的平均成功查找长度。

列表

【2010-THU-Mid】无论有序向量或有序列表，最坏情况下均可在O(logn)时间内完成一次查找。（√）

跳表

【2013-THU-Fin】n个节点的跳转表期望高度为O(logn)。（√）

【2013-THU-Fin】跳转表若变成投掷骰子上面为六才上升一层，则纵向移动变大。（×）

【2014-THU-Fin】跳转表若变成投掷骰子上面为六才上升一层，对于同样存放n个元素的跳转表而言，（A）的期望值将有所增长，但仍保持O(1)。
A. 查找过程中，在同一高度连续跳转的次数
B. 查找过程中，由“向右”到“向下”转折的次数
C. 查找过程中，沿同一座塔连续下行的层数
D. （在查找定位之后）为创建一座新塔所需的时间

【2016，2018-THU-Fin】在n个节点的跳转表中，塔高的期望值为Θ(logn)。（√） 

栈与队列

【2010-THU-Mid】对不含括号的中缀表达式求值时，操作符栈的容量可以固定为某一常数。（√）

操作符栈里最多2个元素

【2010-THU-Mid】RPN中各操作数的相对次序，与原中缀表达式完全一致。（√）

语法分析树的中序遍历序列和后序遍历序列

【2010-THU-Mid】共有（C）种栈混洗方案，可使字符序列{'x', 'o', 'o', 'o', 'x'}的输出保持原样。
A. 12

B. 10

C. 6

D. 5

1. push pop | push pop push pop push pop | push pop
2. push pop | push push pop pop push pop | push pop
3. push pop | push pop push push pop pop | push pop
4. push pop | push push push pop pop pop | push pop
5. push pop | push push pop push pop pop | push pop
6. push push push push push pop pop pop pop pop

【2010-THU-Mid】考查表达式求值算法。算法执行过程中的某时刻，若操作符栈中的括号多达 2010 个，则此时栈的规模（含栈底的'\0'）至多可能多大？试说明理由，并示意性地画出当时栈中的内容。

至多6033个

[ \0, +, *, (, +, *, (, +, *, ... >

【2018-912】非法表达式(12)3+!4*+5执行evaluate算法后的结果为（89）。

输入缓冲	操作数栈	操作符栈	动作
(12)3+!4*+5$		$	识别到开始符
12)3+!4*+5$		$ (	识别到(，栈顶为$，栈顶<当前，(入栈
)3+!4*+5$	12	$	12入栈（readNumber函数识别最长操作数字符串）
3+!4*+5$	12	$	识别到)，栈顶为(，脱括号，推进一个字符
+!4*+5$	12 3	$	3入栈
!4*+5$	12 3	$ +	+入栈
4*+5$	12 3	$ + !	识别到!，栈顶为+，栈顶<当前，!入栈
*+5$	12 3 4	$ + !	4入栈
*+5$	12 3 24	$ +	识别到*，栈顶为!，栈顶>当前，执行!
+5$	12 3 24	$ + *	识别到*，栈顶为+，栈顶<当前，*入栈
+5$	12 72	$ +	识别到+，栈顶为*，栈顶>当前，执行*
+5$	84	$	识别到+，栈顶为+，栈顶>当前，执行+
5$	84	$ +	+入栈
$	84 5	$ +	5入栈
$	89	$	识别到$，栈顶为+，栈顶>当前，执行+
$	89		识别到$，栈顶为$，栈顶=当前，$出栈
$	89		操作符栈为空，while循环退出，得89

【2019-THU-Mid】共有（B）种栈混洗方案，可使序列<MAMAMIA]=A转换为[MAMAMIA>=B。

A. 6

B. 7

C. 8

D. 9

以下操作均为辅助栈C操作

只考虑MAMAM的栈混洗序列，因为IA只有一种可能

画决策树

1. push pop push pop push pop push pop push pop
2. push pop push push push pop pop pop push pop
3. push pop push push push pop push pop pop pop
4. push push push pop push pop push pop pop pop
5. push push push pop pop push push pop pop pop
6. push push push pop pop pop push push pop pop
7. push push push push push pop pop pop pop pop

【2019-THU-Mid】试将常规表达式“(0!+1)*2^(3!+4)+5!/6*(7-8)-9”转化为逆波兰表达式。

0 ! 1 + 2 3 ! 4 ! ^ * 5 !  6 / 7 8 - * 9 -

【2020-THU-Mid】试将常规表达式“(0!+1)*2^(3!+4)-(5!/6+(7-(8-9)))”转化为逆波兰表达式。

散列表

【2010-THU-Fin】设散列表H[]容量M=7，采用除留余数法（H(key) = key % M）确定地址，采用单向平方探测法解决冲突，即 H1 = (H(key) + 1^2) % M，H2 = (H(key) + 2^2) % M，……，Hk = (H(key) + k^2) % M，……。现从空表开始依次插入关键码{2010, 7, 4, 0}，试给出生成的散列表。

H[]	0	1	2	3	4	5	6
key	7	2010	0		4

【2012-THU-Fin】

【2014，2016-THU-Fin】相对于除余法，MAD法在（BC）方面有所改进。
A. 计算速度
B. 高阶均匀性
C. 不动点
D. 满射性
E. 以上皆非

【2014-THU-Fin】（BEF）属于针对闭散列策略的冲突排解方法。
A. mutiple slots
B. linear probing
C. overflow area
D. separate chaining
E. quadratic probing
F. double hashing

【2014，2016-THU-Fin】采用双向平方试探策略时，将散列表长度取作素数𝑀 = 4𝑘 + 3，可以极大地降低查找链前𝑀个位置冲突的概率，但仍不能杜绝。（×） 

【2016，2017-THU-Fin】若元素理想随机，则用除余法作为散列函数时，即使区间长度不是素数，也不会影响数据的均匀性。（×）

【2017-THU-Fin】长为2017的哈希表，使用单向平方试探，若在某次插入时无法找到空桶而必须扩容，此时哈希表中可能的数据个数有（不考虑正在插入的元素）（CD）
A.1005
B.1008
C.1013
D.1018

【2016，2018-THU-Fin】对闭散列 [0, 𝑀), 𝑀 = 2^𝑆 , 采用如下冲突排列解决方法:

• 初始时，𝑐 = 𝑑 = 0
• 探查key冲突时，𝑐 ← 𝑐 + 1，𝑑 ← 𝑑 + 𝑐，探查 H[(key + 𝑑)%𝑀]
则这种算法是否可以保证空间能被 100% 利用？若是，请给出证明；若不是，请举出反例。

【2018-THU-Fin】采用单向平方策略的散列表，只要长度M不是素数，则每一组同义词在表中都不会超过⌊M/2⌋个。（√）
M不是素数时，完全平方数关于M的同余类数量不大于⌊M/2⌋ 

【2018-THU-Fin】将n个词条逐个插入一个容量为M、采用线性试探策略、初始为空的散列表，n<M，则无论它们的插入次序如何，最终的平均成功查找长度都必然一样。（√）
（平方试探有反例） 

【2020-THU-Fin】

字符串匹配

【2010-THU-Mid】在对二进制串做匹配时，采用next[]表比采用BC[]表通常效率更高。（√）

 【2010-THU-Mid】分别计算以下模式串的next[]表、改进的next[]表以及BC[]表。

j	0	1	2	3	4	5	6
P[]	B	A	R	B	A	R	A
next[]	-1	0	0	0	1	2	3
改进的next[]	-1	0	0	-1	0	0	3
BC[]				B		R	A

j	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
P[]	T	A	R	S	O	M	E	_	T	A	T	A	R	S	U	S
next[]	-1	0	0	0	0	0	0	0	0	1	2	1	2	3	4	0
改进的next[]	-1	0	0	0	0	0	0	0	-1	0	2	0	0	0	4	0
BC[]					O	M	E	_			T	A	R		U	S

【2012-THU-Fin】字符集规模越大的时候，next表比BC表效果越好。（×）  

 【2012-THU-Fin】在KMP匹配的过程中，当主程序运行到i, j的状态时，意味着之前至少做过i次成功匹配以及i-j次失败匹配。（×）

可能一直失败，从来没有成功过

【2013-THU-Fin】写出mamammi的改进后next表。 

j	0	1	2	3	4	5	6
改进的next[]	-1	0	0	0	0	3	1

【2013-THU-Fin】写出ladygaga的GS表。 

j	0	1	2	3	4	5	6	7
GS[]	8	8	8	8	8	2	2	1

【2013-THU-Fin】字符集变大，各字符等概率分布，则bc表比next表好。（√）

【2014-THU-Fin】在BM算法中，对于任意模式串P，0<gs[j]≤j对每个0≤j<|P|都成立。（×） 

 【2016-THU-Fin】若KMP算法不使用改进版的next表，最坏情况下时间复杂度可能达到𝑂(𝑚𝑛)。（×）

【2016-THU-Fin】对小写字母集的串匹配，KMP 算法与蛮力算法在（A）情况下渐进的时间复杂度相同。
A. 最好
B. 最坏
C. 平均
D. 以上皆非 

【2016-THU-Fin】对随机生成的m位二进制串，gs 表中 gs[0] = 1 的概率为（）。

【2017-THU-Fin】红鲤鱼与路鲤鱼与路的拼音（HongLiYuYuLuLiYuYuLu）的gs表中有（）项互异项。
(A)3
(B)5
(C)7
(D)以上都不对

【2017，2018-THU-Fin】BM 算法仅仅使用 bc 表或者 gs 表，能够在最好情况下达到 O(n/m) 。（√） 

【2018-THU-Fin】相对KMP算法而言，BM算法更适合于大字符集的应用场合。（√） 

【2020-THU-Fin】试分别给出如下模式串对应的next[]表和改进后的next[]表。

j	0	1	2	3	4	5	6	7	8	9	10	11	12
P[j]	C	B	C	B	A	C	D	C	B	F	B	E	A
next[j]
improvedNext[j]

二叉树

【2010-THU-Mid】所有叶节点深度一致的有根二叉树，必为满树。（）

【2010-THU-Mid】完全二叉树的子树，也一定是完全二叉树。（）

【2010-THU-Mid】由合法的先序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。（√）  

【2010-THU-Mid】在Huffman算法过程中，权重小的内部节点必然早于权重大的内部节点被创建。（） 

【2010-THU-Mid】由6个节点组成的二叉树，若中序遍历序列为ABCDEF，则不可能的后序遍历序列是（）
A. CBEADF

B. ADFECB

C. ABDECF

D. BDACFE

E. 以上皆非

【2010-THU-Mid】由2010个节点组成的完全二叉树，共有（）个叶节点。

【2010-THU-Mid】在由2010个节点组成的二叉树中，若单分支节点不超过10个，则对其做迭代式中序遍历时辅助栈的容量为（）即足够。 

【2010-THU-Mid】某二叉树有 A~G 共 7 个节点，其先序遍历、后序遍历序列的部分内容如下，试将其补全。

先序遍历	E	C		B	D		F
后序遍历	B	A				G

【2019-THU-Mid】由2019个无差别节点构成的真二叉树，与由1009对括号构成的合法表达式一样多。（） 

【2019-THU-Mid】在最优PFC树中交换深度不同的两棵子树，得到的必然不再是最优PFC树。（）

【2019-THU-Mid】同一棵二叉树的前序、中序、后序遍历序列中，叶子节点的相对次序必然完全一致。（）

 【2019-THU-Mid】使用容量为1009的辅助队列，足以对任一由2019个节点构成的二叉树做层次遍历

【2019-THU-Mid】所有内部节点均满足“左子树比右子树高一层”的二叉树，称作Fibonacci树。
1) 试画出其中高度为4者，并从0开始按中序遍历次序对各节点编号；
2) 试给出该树的层次遍历序列。

【2024-912】将以x为根的子树节点个数记为x.size，如果将二叉树中满足x.size * 2  <= x.parent.size的非根节点x称作“轻节点”，那么在包含2024个节点的二叉树中，一个节点至多可能有（）个轻的真祖先。

显然满二叉树每个节点都是轻节点。高度为10的满二叉树有1023个节点，高度为11的满二叉树有2047个节点。考虑对应的2024个节点的完全二叉树，那么根节点左子树的所有节点都是轻节点，左子树的叶节点有9个真祖先是轻节点。

如果某个叶节点有10个真祖先是轻节点，那么这个节点深度至少是11。
如果深度是11，其所在根节点的子树是高度为10的满二叉树，与所在根节点子树的根节点是轻节点矛盾。
其他深度同理可证

【2024-912】出现频率为{1,2,3,3}的一组字符共有（）种PFC编码方案。

频率无用。4个字符需要2位0-1码，共4×3×2×1=24种方案。

搜索树

二叉搜索树

【2010-THU-Mid】由同一组互异关键码，按不同次序逐个插入而生成的 BST 必互异。（）

【2010-THU-Mid】BST中新插入的节点，必是叶节点。（）

【2010-THU-Mid】 由5个互异节点组成、先序遍历序列与层次遍历序列相同的BST，共有（）棵。  

【2014-THU-Fin】由同一组共n个词条构成的任意两棵BST，经O(logn)次zig和zag旋转之后，必可相互转换。（×）

【2016-THU-Fin】在BST中删除两个节点(7B3)，则无论先删除哪个节点，最终BST的拓扑结构均相同。（） 

【2016-THU-Fin】在BST中查找365，以下查找序列中不可能出现的是（）
A. 912,204,911,265,344,380,365
B. 89,768,456,372,326,378,365
C. 48,260,570,302,340,380,361,365
D. 726,521,201,328,384,319,365

【2016-THU-Fin】在不改变 BST 和 BinNode 定义的前提下（BinNode 仅存储 parent, data, lc, rc), 设计算法, 使得从节点 𝑥 出发, 查找值为 𝑌 的节点 𝑦 的时间复杂度为 𝑜(𝑑), 𝑑 为节点 𝑥与 𝑦 的距离。要求利用树的局部性, 复杂度与总树高无关, 否则将不能按满分起评。
函数定义式: 参量为 BinNode 𝑥, 𝑦, 𝑇, 返回值为 BinNode 类型, 函数名 fingerSearch
(a) 说明算法思路
(b) 写出伪代码
(c) 在图中画出由值为 6 的点查找值为 17 的点的查找路径
(d) 说明算法时间复杂度为 𝑂(𝑑) （若无法达到, 说明困难在哪）

【2016，2017-THU-Fin】由5个互异节点构成的不同的BST共有（）个。
A. 24
B. 30
C. 36
D. 42
E. 120

【2018-THU-Fin】若调用BST::remove(e)将节点x从常规BST中删除，则所需的时间为被删除之前x的深度。（×）

平衡二叉搜索树

【2013-THU-Fin】两棵key值顺序一样的BBST经过O(logn)次zig、zag就能互相转化。（）

AVL树

【2010-THU-Mid】在AVL树中删除节点之后若树高降低，则必然做过旋转调整。（×）

【2010-THU-Mid】在包含 2010 个节点的 AVL 树中，最高与最低叶节点之间的深度差最大可达（）。
A. 8

B. 9

C. 10

D. 11

E. 以上皆非

【2010-THU-Mid】右图有可能是一棵刚做过BST的（）操作，但尚未旋转调整的AVL树。

A. delete(2)

B. insert(3)

C. detele(4)

D. insert(5)

E. insert(8) 

【2010-THU-Mid】由2010节点组成的AVL树，最大高度可达（）

【2010-THU-Mid】在高度为2010的AVL树中删除一节点，至多可能造成（）个节点失衡，至多需做（）次旋转调整。 

【2010-THU-Mid】在（）中，越深的节点必然越多。
A. 二叉树

B. AVL树

C. 满二叉树

D. 完全二叉树

E. 以上皆非

【2010-THU-Mid】节点x的父节点和祖父节点分别记作p和g。试在下图中补充尽可能少的节点以构造一棵AVL树，使得：
1) 在摘除x之后，p失衡；

2) 经局部双旋调整之后，g 因失衡需再次实施双旋调整。
请同时在右侧画出最终恢复平衡的树形。 

【2012-THU-Fin】将[1481,1992]区间内的整数逐一插入到空AVL树中，最后该AVL树的高度是（CD）
A. 7 
B. 8 
C. 9 
D. 10 
E. 以上都不对
共512=2^9个元素，至少为9。fib(13)-1=232，也可能是10。

【2013-THU-Fin】依次将 0, ..., 2^d−1插入到初始为空的AVL一定高度为d。（）

【2014-THU-Fin】设在某新节点插入AVL树后（尚待平衡化时），最低失衡节点为g。若此时g的左、右孩子的平衡因子分别为-1和0，则应通过（C）旋转使之重新恢复平衡。 
A. zig
B. zig+zag
C. zag+zig
D. zag
E. 不确定

【2016-THU-Fin】若AVL树插入元素的过程中发生了旋转操作，则树高必不变。（√）

【2016-THU-Fin】如果元素理想随机，那么对二叉搜索树做平衡化处理，对改进其渐进时间复杂度并没有什么实质的作用。（×）

【2018-THU-Fin】在某节点被删除后AVL树的高度即便下降了，这次操作期间也未必做过旋转调整。（√）

【2018-THU-Fin】对规模为n的AVL树做一次插入操作，最坏情况下可能引发\omega(logn)次局部重构。（×）

时间复杂度为O(logn)，但只有不多于1次局部重构

伸展树

【2010-THU-Mid】设x为某伸展树中的最大关键码，则在find(x)过程中不可能实施（）调整。
A. zig‐zig

B. zig‐zag

C. zag‐zig

D. zag‐zag

E. 以上皆非

【2013-THU-Fin】将2014个数插入splay，第一次访问经过2013次旋转，则是单调插入的。（） 

【2014-THU-Fin】即便访问序列不满足局部性（比如完全理想的随机），伸展树依然能保证分摊O(logn)的性能。（√）

【2016-THU-Fin】在任何情况下，伸展树总能保持每次操作𝑂(log 𝑛)的平均复杂度。（） 

【2018-THU-Fin】只有在访问序列具有较强的局部性时，伸展树才能保证分摊O(logn)的性能。（）

【2018-THU-Fin】将{0,1,...,2018}插入一棵空的伸展树后，若树高为2018，则上述词条必是按单调次序插入的。（）

【2018-THU-Fin】最底层的叶节点一旦被访问（并做过splay调整）之后，伸展树的高度必然随即下降。（）

红黑树

【2012-THU-Fin】对红黑树进行插入操作时，进行双红修正，黑高度增加，则（）发生重染色，（）发生结构调整。
A. 必然，必然
B. 必然，可能
C. 必然，必然不
D. 可能，必然
E. 可能，可能
F. 可能，必然不

【2013-THU-Fin】在初始为空的红黑树中依次插入关键码[0, N)
（1）写出N = 9的红黑树
（2）写出树高 H 和 N 的通项公式

【2016-THU-Fin】若红黑树插入一个元素后，黑高度增加，则双红修正过程中没有拓扑结构变换，只有重染色操作。（）

【2018-THU-Fin】红黑树的插入或删除操作，都有可能导致\omega(logn)个节点的颜色反转。（）

【2018-THU-Fin】在插入操作后若红黑树黑高度增加，则在双红修复过程中仅做过重染色，而无任何结构调整。（）

B-树

【2010-THU-Mid】高度为3的5阶B‐树，至多可存放（）个关键码，至少需存放（）个。

【2012-THU-Fin】将[23,1481)区间内的整数组成一个2-3-B树，且根节点只有一个关键码，则最终该B树的高度至少是（）
A. 7
B. 8
C. 9
D. 以上都不对

【2014-THU-Fin】Btree::solveOverflow()和 Btree::solveUnderflow()在最坏情况下均需Ω(logn)时间。然而在 B-树任一足够长的生命期内，就分摊意义而言二者都仅需O(1)时间。（）

【2016-THU-Fin】将𝑁个关键码按随机次序插入B树，则期望的分裂次数为𝑂 (log^2𝑁)。（）

【2016-THU-Fin】以下数据结构，在插入元素后可能导致𝑂(log 𝑛)次局部结构调整的是（）
A. AVL 
B. B-树 
C. 红黑树 
D. 伸展树 
E. 以上皆非

【2016-THU-Fin】人类拥有的数字化数据数量，在2010年已达到ZB (2^70 = 10^21) 量级。若每个字节自成一个关键码，用一棵16阶B-树存放，则可能的高度为（）
A. 10
B. 20
C. 40
D. 80
E. 大于80

【2017-THU-Fin】B树非叶节点的元素都有后继元素，且都在叶子节点中。（）

【2012，2017-THU-Fin】对以下各种搜索树进行删除操作，哪些树可能会经过Ω(logn)次局部调整，其中n为关键码的数量。（）
A. AVL
B. 伸展树
C. 红黑树
D. B-树
E. 都不会

【2017-THU-Fin】一个初始时只有一个内部节点的10阶B树，经过9900次分裂和7888次合并，节点数可能在（）附近。
A. 2013
B. 2015
C. 2017
D. 2018

【2018-THU-Fin】考查包含2018个关键码的16阶B-树，约定根节点常驻内存，且在各节点内部采用顺序查找。

a) 在单次成功查找的过程中，至多可能需要读多少次磁盘？

b) 在单次成功查找的过程中，至多可能有多少个关键码需要不目标关键码做比较？

【2018-THU-Fin】B-树的任一非叶节点内，每个关键码都存在直接后继，且必然来自某个叶节点。（）

【2020-THU-Fin】如何从B-树中删除一个属于内部节点而非叶节点的关键码？

kd树

【2016-THU-Fin】在 kd-search中，查找区间𝑅与任一节点的 4个孙节点（假设存在）对应区域最多有 2 个相交。（）

【2014，2016-THU-Fin】以下数据结构中，空间复杂度不超过线性的有（）
(A)2d-tree
(B)3d-tree
(C)2D range tree
(D)interval tree
(E)segment tree
(F)priority search tree

优先级队列

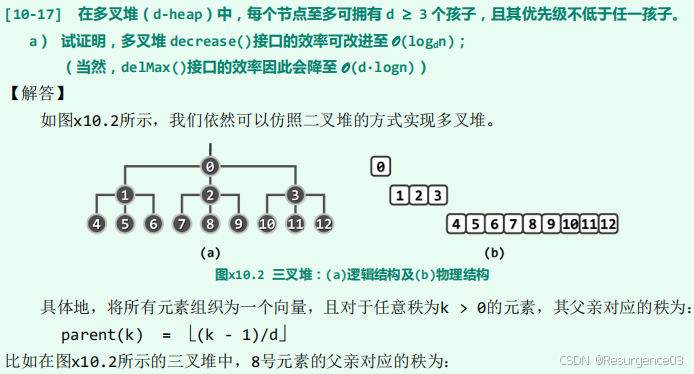
【2013-THU-Fin】多叉堆比二叉堆插入慢，删除快。（×） 

【2013-THU-Fin】对于关键码为0,1,…,2014的左式堆。

1. 左子堆至少有几个节点（不包括外部节点）,右子树最高多高？
2. 画出示意图。
3. 按什么顺序插入0..2014，能成为2中图的样子？

【2014-THU-Fin】对于二叉堆，尽管多叉堆的高度更低，但无论是下滤一层还是整个下滤过程，时间成本反而都会增加。（×）

【2014-THU-Fin】对于任何一棵二叉树T，其右、左子树的规模之比称为右偏率。对于（常规）高度同为h的AVL树（A），红黑树（R），左式堆（L），若分别考查其右偏率所能达到的最大值，则在h足够大之后，三者按此指标的排列次序应是（C）
A. L<R<A
B. L<A<R
C. R<A<L
D. A<R<L
E. 以上皆非 

【2016-THU-Fin】与二叉堆相比，多叉堆delMax()操作时间复杂度更高。 （×）

【2016-THU-Fin】完全二叉堆删除元素在最坏情况下时间复杂度为O(logn)，但平均情况下仅为O(1)。（×）

【2013，2016-THU-Fin】在使用Heapify批量建堆的过程中，改变同层节点的下滤次序对算法的正确性和时间效率都无影响。（√）

【2016-THU-Fin】二叉堆中某个节点秩为𝑘, 则其兄弟节点（假设存在）的秩为（AB）

A. 𝑘 + 1
B. 𝑘 − 1
C. 𝑘 + (−1)^𝑘
D. 𝑘 − (−1)^𝑘
E. 以上皆非

 【2016-THU-Fin】有2015个节点的左式堆，左子堆最小规模为（E）（不计外部节点）
A. 10
B. 11
C. 1007
D. 1008
E. 以上皆非

【2017-THU-Fin】当输入是理想随机的时候堆的delMax的平均复杂度是O(1)，尽管最坏是 O(logn)。（×）

【2016，2017-THU-Fin】对于左式堆A和B，合并后所得二叉堆的右侧链元素一定来自A和B的右侧链。（×）  

【2017-THU-Fin】给了一种数据结构 DEPQ（双端优先队列），空间上是线性，能够 O(1)的时间获得序列的最大值最小值，O(logn)的时间 delMin、delMax、insert
(1)如果序列的长度超过了内存，请利用这种数据结构借鉴快速划分策略给出一种排序算法
(2)如果总序列长度是 1TB，内存是 2GB，IO 页面是 4KB，单次比较操作、内存读取的时间是 t，IO 延时是 2^17t，请估计你的算法在最好最坏的情况下的时间
(3)请给出一些改进平均性能的策略

【2018-THU-Fin】相对于同样规模的完全二叉堆，多叉堆delMax()操作的时间成本更低。（×）

【2018-THU-Fin】左式堆中每一对兄弟节点的高度尽管未必“左大右小”，但左兄弟至少不低于右兄弟的一半。（×）

【2018-THU-Fin】采用Crane算法将左式堆A与B合并为左式堆H，右侧链上的节点未必都来自A或B的右侧链。（√）

图

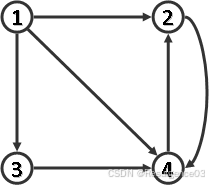
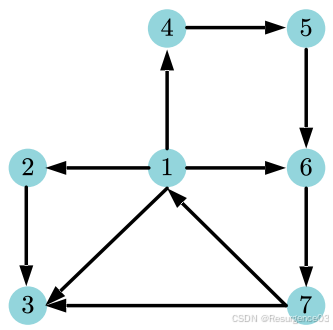
 【2010-THU-Fin】某有向图的邻接矩阵如下，现从顶点1出发做DFS遍历，遇多顶点歧义时编号小者优先。试在表标出各边的分类结果（树边T，前向边F，后向边B，跨边C）

	1	2	3	4
1
2
3
4

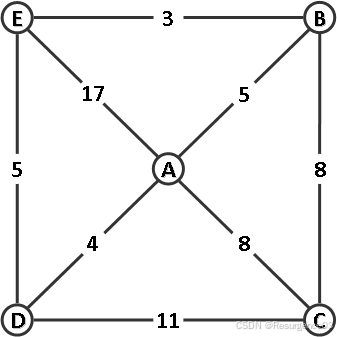
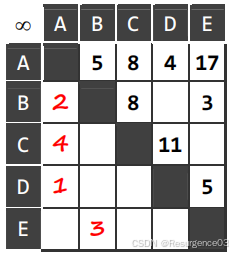
 【2010-THU-Fin】某无向网络及其邻接矩阵的上三角部分如下，现从顶点 A 出发采用 Prim 算法构造最小生成树，试在下三角区域标出树边及其被选用的次序。遇多边歧义时，按边端点合成数的字典序小者优先。 

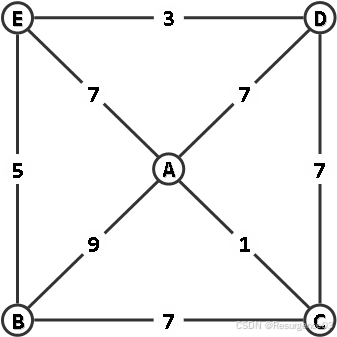
 【2010-THU-Fin】某无向网络及其邻接矩阵的上三角部分如下。现从顶点 A 出发采用 Dijkstra 算法构造最短路径生成树，试在下三角区域标出树边及其被选用的次序。遇多边歧义时，按边端点合成数的字典序小者优先。 

【2012-THU-Fin】对于正权值有向图，如果把所有的边权都平方之后，Dijkstra算法得到的最短路径树不变。（√）  

【2012-THU-Fin】对于7节点的有向图，节点标号为1 ∼ 7，指定当存在歧义性的时候优先考虑标号小的节点。一共有多少条树边，跨边，前向边和后向边？

【2013-THU-Fin】BFS，DFS的复杂度可能不是O(N + E)。（）

【2013-THU-Fin】PFS每次调用priorUpdata()，总复杂度O(n)。（） 

【2014-THU-Fin】我们知道，因同一顶点的邻居被枚举的次序不同，同一有向图 G 所对应的 DFS 森林未必唯一。然而只要起始于 G 中某顶点 s 的某次 DFS 所生成的是一棵树，则起始于 s 的任何一次 DFS 都将生成一棵树。（）

【2014-THU-Fin】在无向连通图G中选定一个顶点 s，并将各顶点v到s的距离记作dist(v)（特别地，dist(s)=0）。于是在G.BFS(s)过程中，若辅助队列为Q，则dist(Q.front()) + 1 ≥ dist(Q.rear())始终成立。（√） 

【2014-THU-Fin】有向图的DFS不仅起点任意，而且每一步迭代往往都会有多个顶点可供选择，故所生成的DFS森林并不唯一确定，且其中所含（）的数量也可能不同。
A. 树边
B. 前向边
C. 后向边
D. 跨越边
E. 以上皆非

【2016-THU-Fin】如果把朋友圈视为一无向图，那么即使A君看不到你给B点的赞，你们仍可能属于同一个双联通分量。（√）

【2014，2016-THU-Fin】在有向图G中，存在一条自顶点v通向u的路径，且在某次DFS中有dTime[v]<dTime[u]，则在这次DFS所生成的DFS森林中，v必是u的祖先。（×） 

【2017-THU-Fin】用堆实现 PFS 时元素的深度只会减少不会增加。（）

【2017-THU-Fin】PFS 时调用 priorityUpdater 至多 O(e)次。（）

【2018-THU-Fin】在图DFS()算法中的default分支，将dTime(v) < dTime(u)改为dTime(v) < fTime(u)同样可行。（） 

【2013，2018-THU-Fin】有向图经DFS后若共有k条边被标记为BACKWARD，则它应恰有k个环路。（×） 

【2018-THU-Fin】对于同一无向图，起始于顶点s的DFS尽管可能得到结构不同的DFS树，但s在树中的度数必然固定。（）

【2016，2018-THU-Fin】在图的优先级搜索过程中，每次可能调用多次prioUpdater，但累计调用次数仍为O(e)。（）

【2018-THU-Fin】若用完全二叉堆来实现PFS，则各顶点在出堆之前，深度只可能逐步减少（或保持）而不致增加。（）

排序

【2010-THU-Mid】只要是采用基于比较的排序算法，对任何输入序列都至少需要运行O(nlogn)时间。（√）  

【2010-THU-Mid】若借助二分查找确定每个元素的插入位置，向量的插入排序只需O(nlogn)时间。（） 

【2010-THU-Mid】考查如下问题：任给12个互异的整数，且其中10个已组织为一个有序序列，现需要插入剩余的两个以完成整体排序。若采用基于比较的算法（CBA），最坏情况下至少需做几次比较？为什么？

【2010-THU-Mid】向量的插入排序由n次迭代完成，逐次插入各元素。为插入第k个元素，最坏情况需做k次移动，最好时则无需移动。从期望的角度来看，无需移动操作的迭代平均有多少次？为什么？假定各元素是等概率独立均匀分布的。

 【2010-THU-Fin】对整型向量[16,2011,6]做就地堆排序，试给出堆初始化（Robert Floyds 算法）以及各次迭代之后向量的内容。

Rank	0	1	2
Vector	16	2011	6
Heap	2011	16	6
1	16	6	2011
2	6	16	2011
3	6	16	2011

加粗为Sorted部分

【2013-THU-Fin】shell排序若将（底层的排序从）插入排序改成归并排序，效率会变快。（）

【2013-THU-Fin】radix 排序将桶排序改成quick排序，仍然正确。（×） 

【2013-THU-Fin】因为取（步长序列为）1,2,4,8, … , 2^𝑛会产生最坏情况
1、（步长序列变成）1,3,7, … , 2^𝑛 − 1会如何？
2、（步长序列变成）1,5,9,17, … , 2^𝑛 + 1会如何？  

【2014-THU-Mid】 不存在CBA式算法，能够经过少于2n-3次比较操作，即从n个整数中找出最大和次大者。（） 

 【2014-THU-Mid】存在CBA式算法，能够在O(n)时间内从n个无序整数中找出最大的10%。 

【2014-THU-Fin】无论 g 和 h 互素与否，已知 h-有序的序列再经过 g-排序之后，必然继续保持 h-有序。（）

【2014-THU-Mid】 起泡排序的每一趟扫描交换中若有元素发生交换，则相邻的逆序对必然减少。（）  

【2016-THU-Fin】既然可以在𝑂(𝑛)时间内找出𝑛个数的中位数，快速排序算法（12-A1）即可优化至𝑂(𝑛log 𝑛)。（）

【2016-THU-Fin】若序列中逆序对个数为𝑂(𝑛2),则使用快速排序（12-A1）须进行的交换次数为𝑂(𝑛log 𝑛)。（）

【2016-THU-Fin】与胜者树相比，败者树在重赛过程中，需反复将节点与其兄弟进行比较。（×） 

【2017-THU-Fin】底层排序的稳定性保证了radixsort的正确性和稳定性。（√）  

【2017-THU-Fin】当待排序列的长度超过内存的时候，（）序列的shell排序速度最慢。

A. Shell
B. PS
C. Pratt
D. Sedgewick

【2017-THU-Fin】ℋshell = {1,2,4,8,16,32,64, … , 2^𝑘, … },设以下两种步长序列分别为ℋshell-改进 1 ={1,3,5,9,17, … , 2^𝑘 + 1, … }和ℋshell-改进 2 = {1,3,7,15,31, … , 2^𝑘 − 1,… }，哪种能必然避免O(n²)的最坏情况。（）
A. 只有ℋshell-改进 1能避免
B. 只有ℋshell-改进 2能避免
C. ℋshell-改进 1和ℋshell-改进 2都能避免
D. ℋshell-改进 1和ℋshell-改进 2都不能避免 

【2018-THU-Fin】若输入序列包含\omega(n^2)个逆序对，则快速排序算法（ LUG版）至少需要执行O(nlogn)元素交换操作。（） 

【2018-THU-Fin】经快速划分（LGU版）之后，后缀中的雷同元素可能调换相对次序，但其余部分的雷同元素绝不会。（）

 【2018-THU-Fin】只要底层的排序算法是正确且稳定的，则RadixSort也必然是正确且稳定的。（√） 

【2018-THU-Fin】采用任何一种增量序列， Shell排序最后的1-sorting都只需要O(n)时间。（）

【2018-THU-Fin】Shell排序每按照某个增量做过逐列排序，序列中逆序对的总数都会减少（或持平），但绝不致增加。（）

【2018-THU-Fin】胜者树的根节点即是冠军，而败者树的根节点即是亚军。（√）  

【2019-THU-Mid】 插入排序算法的（B）特点，是选择排序算法所不具备的。
A. 输入敏感性

B. 支持在线计算

C. 就地性

D. 最好情况下复杂度更低

选择问题

【2012-THU-Fin】一个向量若存在众数，则该数必然是中位数以及频繁数。（√）

【2012-THU-Fin】如果使用了线性复杂度的中位数选取算法，快速排序的复杂度可以保证在最坏情况下也渐进等于O(nlogn)。（√）

【2013-THU-Fin】在1983个数字中取前三大，最少比较多少次？

【2014-THU-Fin】为从 2014 个随机元素中挑选出最大的 5 个，（ ）在最坏情况下所需的比较操作次数最少。

A. 构建大顶的锦标赛树，再做5次 delMax()
B. 用 Floyd 算法构建大顶堆，再做5次 delMax()
C. 采用选择排序算法，但仅执行前5次迭代
D. 采用起泡排序算法，但仅执行前5次迭代
E. 用 LinearSelect()算法找出第5大的元素，再遍历一趟找出至多4个大于它的元素