概叙

关于文本相似度的判定算法，可参考：科普文：Java基础之算法系列【文本相似度判定算法梳理】-CSDN博客

关于imhash局部敏感哈希算法，可参考：

科普文：【哈希算法的扩展应用：HashRing哈希环、哈希切分、SimHash局部敏感哈希算法、GeoHash经纬度哈希、BloomFilter布隆过滤器、CuckooFilter布谷鸟过滤器等】-CSDN博客

Simhash算法简介

SimHash基本原理是通过一系列的哈希函数将输入的文档转换为一个固定长度的指纹（通常是一个64位的整数）。然后，可以通过计算文档指纹的汉明距离来确定它们的相似度。

汉明距离是指两个字符串对应位置的不同字符的个数。
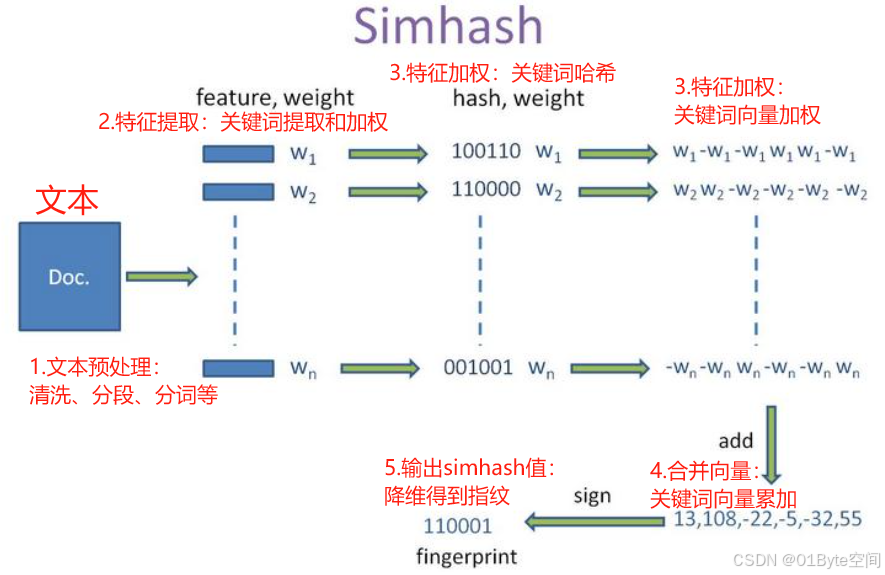
SimHash算法的主要工作是将文本进行降维，生成一个SimHash值，也就是“指纹”。

Simhash原理

其原理包括以下几个关键步骤：

1. ‌文本预处理‌：将文本进行分段、分词、去停用词等操作，生成可比较的词汇序列。
2. ‌特征提取‌：将文本的各种元素（如核心单词、专有名词、句式等）转化为数字，量化文本内容。
3. ‌特征加权‌：对提取的特征进行加权处理，通常使用词频作为权重。
4. ‌生成SimHash值‌：
   1. 对每个特征使用传统的hash算法生成一个f位的签名。
   2. 根据签名的每一位，如果是1则加上该特征的权重，如果是0则减去该特征的权重。
   3. 将得到的向量进行二值化处理，如果某位的值大于0，则该位为1；否则为0。
5. ‌输出SimHash值‌：最终得到的二进制串即为SimHash值。

simhash算法的输入是一个向量，输出是一个 f 位的签名值。

为了陈述方便，假设输入的是一个文档的特征集合，每个特征有一定的权重。

比如特征可以是文档中的词，其权重可以是这个词出现的次数。

simhash 算法如下：

1，将一个 f 维的向量 V 初始化为 0 ； f 位的二进制数 S 初始化为 0 ；

2，对每一个特征：用传统的 hash 算法对该特征产生一个 f 位的签名 b 。对 i=1 到 f ： 如果b 的第 i 位为 1 ，则 V 的第 i 个元素加上该特征的权重； 否则，V 的第 i 个元素减去该特征的权重。

  3，如果 V 的第 i 个元素大于 0 ，则 S 的第 i 位为 1 ，否则为 0 ；

4，输出 S 作为签名。

SimHash算法几何意义和原理

这个算法的几何意义非常明了。

它首先将每一个特征映射为f维空间的一个向量，这个映射规则具体是怎样并不重要，只要对很多不同的特征来说，它们对所对应的向量是均匀随机分布的，并且对相同的特征来说对应的向量是唯一的就行。

比如一个特征的4位hash签名的二进制表示为1010，那么这个特征对应的 4维向量就是(1, -1, 1, -1)T，即hash签名的某一位为1，映射到的向量的对应位就为1，否则为-1。

然后，将一个文档中所包含的各个特征对应的向量加权求和，加权的系数等于该特征的权重。得到的和向量即表征了这个文档，我们可以用向量之间的夹角来衡量对应文档之间的相似度。

最后，为了得到一个f位的签名，需要进一步将其压缩，如果和向量的某一维大于0，则最终签名的对应位为1，否则为0。这样的压缩相当于只留下了和向量所在的象限这个信息，而64位的签名可以表示多达264个象限，因此只保存所在象限的信息也足够表征一个文档了。

明确了算法了几何意义，使这个算法直观上看来是合理的。

但是，为何最终得到的签名相近的程度，可以衡量原始文档的相似程度呢？

这需要一个清晰的思路和证明。

在simhash的发明人Charikar的论文中并没有给出具体的simhash算法和证明，以下列出我自己得出的证明思路。

Simhash是由随机超平面hash算法演变而来的，随机超平面hash算法非常简单，对于一个n维向量v，要得到一个f位的签名(f<<n)，算法如下： 1，随机产生f个n维的向量r1,…rf； 2，对每一个向量ri，如果v与ri的点积大于0，则最终签名的第i位为1，否则为0.

这个算法相当于随机产生了f个n维超平面，每个超平面将向量v所在的空间一分为二，v在这个超平面上方则得到一个1，否则得到一个0，然后将得到的 f个0或1组合起来成为一个f维的签名。如果两个向量u, v的夹角为θ，则一个随机超平面将它们分开的概率为θ/π，因此u, v的签名的对应位不同的概率等于θ/π。所以，我们可以用两个向量的签名的不同的对应位的数量，即汉明距离，来衡量这两个向量的差异程度。

Simhash算法与随机超平面hash是怎么联系起来的呢？

在simhash算法中，并没有直接产生用于分割空间的随机向量，而是间接产生的：第 k个特征的hash签名的第i位拿出来，如果为0，则改为-1，如果为1则不变，作为第i个随机向量的第k维。

由于hash签名是f位的，因此这样能产生 f个随机向量，对应f个随机超平面。

下面举个例子：

假设用5个特征w1,…,w5来表示所有文档，现要得到任意文档的一个3维签名。

假设这5个特征对应的3维向量分别为： h(w1) = (1, -1, 1)T h(w2) = (-1, 1, 1)T h(w3) = (1, -1, -1)T h(w4) = (-1, -1, 1)T h(w5) = (1, 1, -1)T

按simhash算法，要得到一个文档向量d=(w1=1, w2=2, w3=0, w4=3, w5=0) T的签名，

先要计算向量m = 1*h(w1) + 2*h(w2) + 0*h(w3) + 3*h(w4) + 0*h(w5) = (-4, -2, 6) T， 然后根据simhash算法的步骤3，得到最终的签名s=001。

上面的计算步骤其实相当于，先得到3个5维的向量，第1个向量由h(w1),…,h(w5)的第1维组成：

r1=(1,-1,1,-1,1) T； 第2个5维向量由h(w1),…,h(w5)的第2维组成： r2=(-1,1,-1,-1,1) T；

同理，第3个5维向量为： r3=(1,1,-1,1,-1) T. 按随机超平面算法的步骤2，分别求向量d与r1,r2,r3的点积: d T r1=-4 < 0，所以s1=0; d T r2=-2 < 0，所以s2=0; d T r3=6 > 0，所以s3=1.

故最终的签名s=001，与simhash算法产生的结果是一致的。

从上面的计算过程可以看出，simhash算法其实与随机超平面hash算法是相同的，simhash算法得到的两个签名的汉明距离，可以用来衡量原始向量的夹角。

这其实是一种降维技术，将高维的向量用较低维度的签名来表征。衡量两个内容相似度，需要计算汉明距离，这对给定签名查找相似内容的应用来说带来了一些计算上的困难；我想，是否存在更为理想的simhash算法，原始内容的差异度，可以直接由签名值的代数差来表示呢？

SimHash算法的“指纹”比较相似度

海明距离： 两个码字的对应比特取值不同的比特数称为这两个码字的海明距离。

一个有效编码集中, 任意两个码字的海明距离的最小值称为该编码集的海明距离。

举例如下： 10101 和 00110 从第一位开始依次有第一位、第四、第五位不同，则海明距离为 3.

异或： 只有在两个比较的位不同时其结果是1 ，否则结果为 0 

对每篇文档根据SimHash 算出签名后，再计算两个签名的海明距离（两个二进制异或后 1 的个数）即可。根据经验值，对 64 位的 SimHash ，海明距离在 3 以内的可以认为相似度比较高。

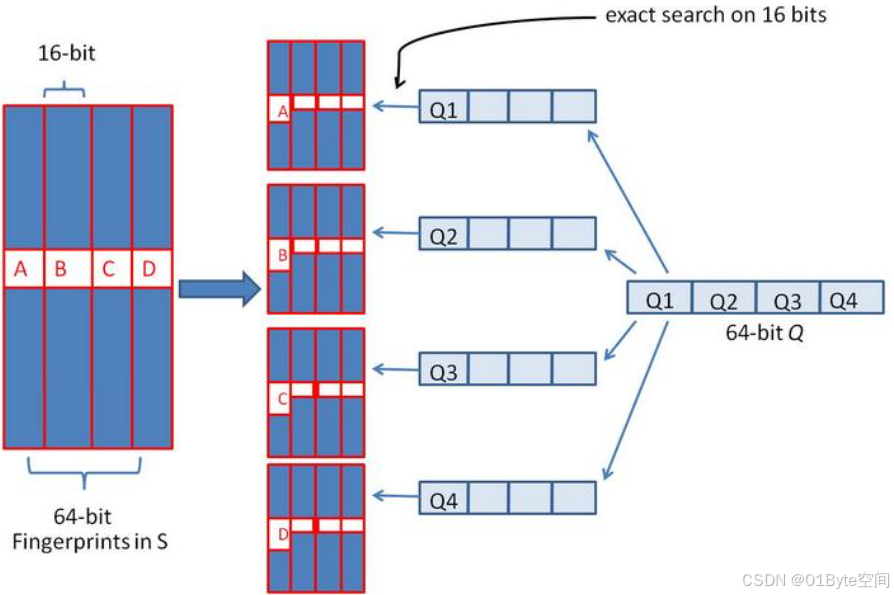
假设对64 位的 SimHash ，我们要找海明距离在 3 以内的所有签名。

我们可以把 64 位的二进制签名均分成 4块，每块 16 位。根据鸽巢原理（也成抽屉原理，见组合数学），如果两个签名的海明距离在 3 以内，它们必有一块完全相同。 我们把上面分成的4 块中的每一个块分别作为前 16 位来进行查找。 建立倒排索引。

如果库中有2^34 个（大概 10 亿）签名，那么匹配上每个块的结果最多有 2^(34-16)=262144 个候选结果 (假设数据是均匀分布， 16 位的数据，产生的像限为 2^16 个，则平均每个像限分布的文档数则 2^34/2^16 = 2^(34-16)) ，四个块返回的总结果数为 4* 262144 （大概 100 万）。

原本需要比较 10 亿次，经过索引，大概就只需要处理 100 万次了。

由此可见，确实大大减少了计算量。 

SimHash的java示例

package com.zxx.study.algorithm.hash.hashplus;


import java.io.IOException;
import java.math.BigInteger;
import java.nio.charset.StandardCharsets;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;

/**
 * @author zhouxx
 * @create 2025-01-01 0:13
 */
public class TestSimHash {

    public static void main(String[] args) {
        // 测试SimHash计算
        String text1 = "This is a simple Chinese text：我爱中国.";
        String text2 = "This is another simple Chinese text example：我爱中国.";

        MessageDigest digest = null;
        try {
            digest = MessageDigest.getInstance("SHA-256");
        } catch (NoSuchAlgorithmException e) {
            e.printStackTrace();
        }
        BigInteger sha_256_1=new BigInteger(digest.digest(text1.getBytes(StandardCharsets.UTF_8)));
        BigInteger sha_256_2=new BigInteger(digest.digest(text2.getBytes(StandardCharsets.UTF_8)));
        int distance = sha_256_1.xor(sha_256_2).bitCount();
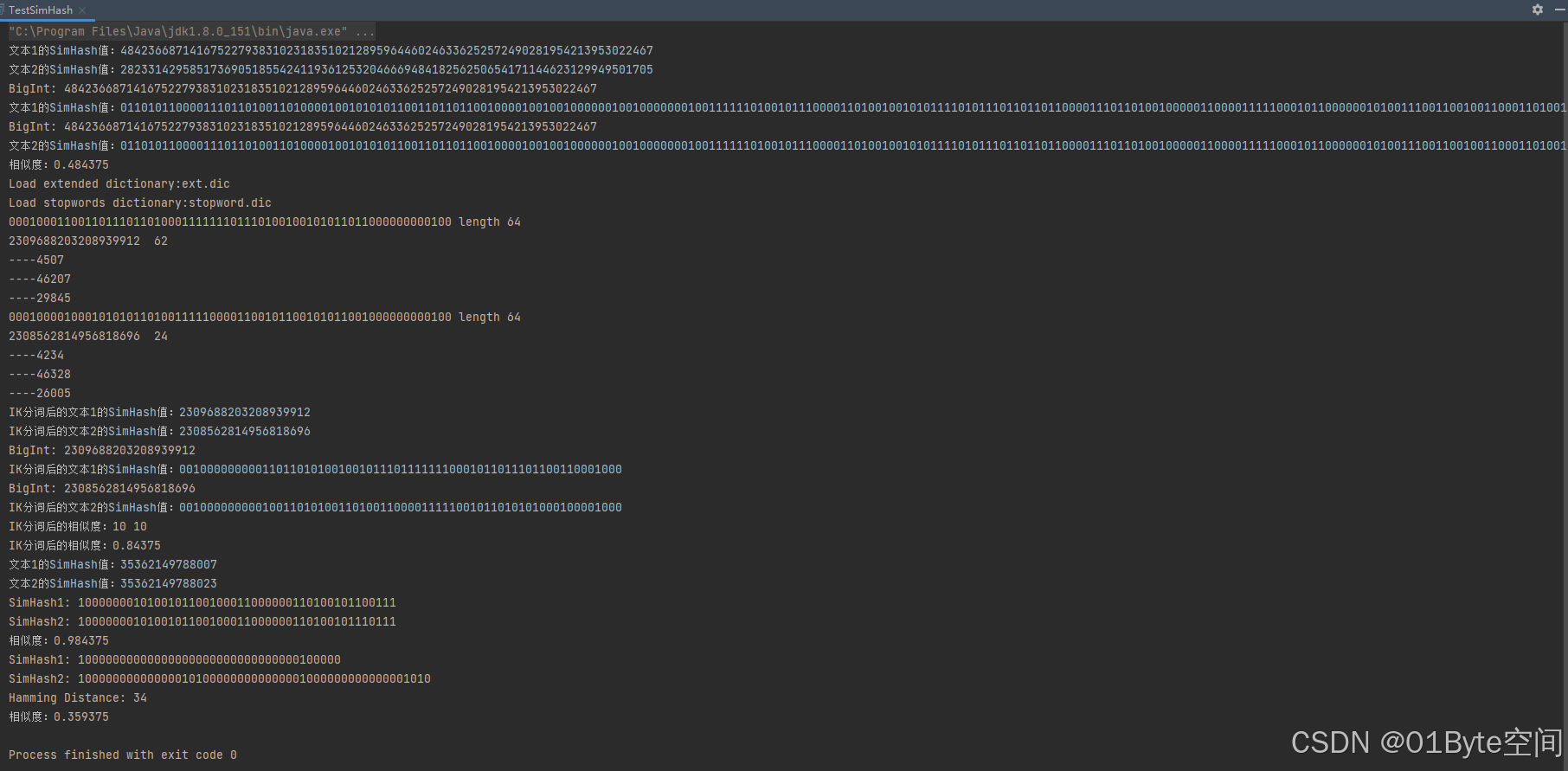
        System.out.println("文本1的SimHash值：" + sha_256_1);
        System.out.println("文本2的SimHash值：" + sha_256_2);
        System.out.println("文本1的SimHash值：" + binaryString(sha_256_1));
        System.out.println("文本2的SimHash值：" + binaryString(sha_256_1));
        System.out.println("相似度：" + (1 - (double) distance / 256));

        try {
            SimHash3 simHash3_1 = new SimHash3(text1, 64);
            System.out.println(simHash3_1.getIntSimHash() + "  " + simHash3_1.getIntSimHash().bitLength());
            // 计算 海明距离 在 3 以内的各块签名的 hash 值
            simHash3_1.subByDistance(simHash3_1, 3);

            SimHash3 simHash3_2 = new SimHash3(text2, 64);
            System.out.println(simHash3_2.getIntSimHash() + "  " + simHash3_2.getIntSimHash().bitCount());
            simHash3_1.subByDistance(simHash3_2, 3);

            int dis = simHash3_1.getDistance(simHash3_1.getStrSimHash(), simHash3_2.getStrSimHash());

            System.out.println("IK分词后的文本1的SimHash值：" + simHash3_1.getIntSimHash());
            System.out.println("IK分词后的文本2的SimHash值：" + simHash3_2.getIntSimHash());
            System.out.println("IK分词后的文本1的SimHash值：" + binaryString(simHash3_1.getIntSimHash()));
            System.out.println("IK分词后的文本2的SimHash值：" + binaryString(simHash3_2.getIntSimHash()));
            System.out.println("IK分词后的相似度："+simHash3_1.hammingDistance(simHash3_2) + " " + dis);
            distance = simHash3_1.getIntSimHash().xor(simHash3_2.getIntSimHash()).bitCount();
            System.out.println("IK分词后的相似度："+ (1 - (double) distance / 64));

        } catch (IOException e) {
            e.printStackTrace();
        }




        SimHash2 simHash = new SimHash2();
        BigInteger hash1 = simHash.simHash(text1);
        BigInteger hash2 = simHash.simHash(text2);
        System.out.println("文本1的SimHash值：" + hash1);
        System.out.println("文本2的SimHash值：" + hash2);
        System.out.println("SimHash1: " + Long.toBinaryString(hash1.longValue()));
        System.out.println("SimHash2: " + Long.toBinaryString(hash2.longValue()));
        System.out.println("相似度：" + simHash.similarity(hash1, hash2));
        /**
         * 文本1的SimHash值：35362149788007
         * 文本2的SimHash值：35362149788023
         * SimHash1: 1000000010100101100100011000000110100101100111
         * SimHash2: 1000000010100101100100011000000110100101110111
         * 相似度：0.984375
         *
         * */

        long simHash1 = SimHash1.SimHash(text1);
        long simHash2 = SimHash1.SimHash(text2);
        System.out.println("SimHash1: " + Long.toBinaryString(simHash1));
        System.out.println("SimHash2: " + Long.toBinaryString(simHash2));
        // 计算汉明距离来评估相似度
        long hammingDistance = simHash1 - simHash2;
        distance = Long.bitCount(hammingDistance);
        System.out.println("Hamming Distance: " + distance);
        System.out.println("相似度：" + SimHash1.similarity(simHash1, simHash2));
        /**
         * SimHash1: 10000000000000000000000000000000100000
         * SimHash2: 100000000000000101000000000000001000000000000001010
         * Hamming Distance: 34
         * 相似度：-0.28125
         * */

    }
    public static String binaryString(BigInteger bigInt){
        byte[] binaryArray = bigInt.toByteArray();
        System.out.print("BigInt: " + bigInt + "\n");
        StringBuilder sb=new StringBuilder();
        for (byte b : binaryArray) {
            sb.append(String.format("%8s", Integer.toBinaryString(b & 0xFF)).replace(' ', '0'));
        }
        return sb.toString();
    }
}

输出结果：

文本1的SimHash值：48423668714167522793831023183510212895964460246336252572490281954213953022467
文本2的SimHash值：28233142958517369051855424119361253204666948418256250654171144623129949501705
BigInt: 48423668714167522793831023183510212895964460246336252572490281954213953022467
文本1的SimHash值：0110101100001110110100110100001001010101100110110110010000100100100000010010000000100111111010010111000011010010010101111010111011011011000011101101001000001100001111100010110000001010011100110010011000110100110111101000010101101100100000000010101000000011
BigInt: 48423668714167522793831023183510212895964460246336252572490281954213953022467
文本2的SimHash值：0110101100001110110100110100001001010101100110110110010000100100100000010010000000100111111010010111000011010010010101111010111011011011000011101101001000001100001111100010110000001010011100110010011000110100110111101000010101101100100000000010101000000011
相似度：0.484375
Load extended dictionary:ext.dic
Load stopwords dictionary:stopword.dic
0001000110011011101101000111111101110100100101011011000000000100 length 64
2309688203208939912  62
----4507
----46207
----29845
0001000010001010101101001111100001100101100101011001000000000100 length 64
2308562814956818696  24
----4234
----46328
----26005
IK分词后的文本1的SimHash值：2309688203208939912
IK分词后的文本2的SimHash值：2308562814956818696
BigInt: 2309688203208939912
IK分词后的文本1的SimHash值：0010000000001101101010010010111011111110001011011101100110001000
BigInt: 2308562814956818696
IK分词后的文本2的SimHash值：0010000000001001101010011010011000011111001011010101000100001000
IK分词后的相似度：10 10
IK分词后的相似度：0.84375
文本1的SimHash值：35362149788007
文本2的SimHash值：35362149788023
SimHash1: 1000000010100101100100011000000110100101100111
SimHash2: 1000000010100101100100011000000110100101110111
相似度：0.984375
SimHash1: 10000000000000000000000000000000100000
SimHash2: 100000000000000101000000000000001000000000000001010
Hamming Distance: 34
相似度：0.359375

Process finished with exit code 0