文章目录
一、集成算法
1.1 概念
集成算法是一种通过组合多个基本模型来提高预测准确度的机器学习技术。这些基本模型可以是同一模型的不同实例,也可以是不同类型的算法。
集成算法的基本思想是将多个模型的预测结果结合起来,以获得更加准确的预测结果。
常见的集成算法包括:Bagging、Boosting、Stacking等。
- Bagging:并行训练多个弱分类器
- Boosting:迭代生成多个弱分类器
Boosting算法:
Bagging算法:
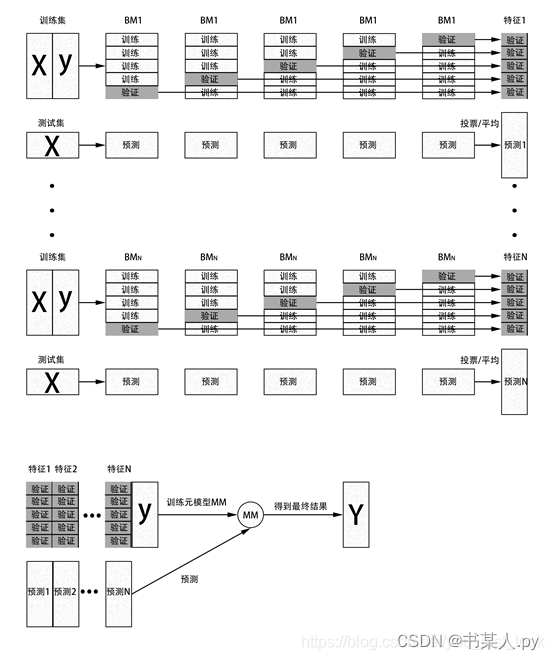
Stacking算法:
现在我们逐一介绍几种常见的集成算法。
1.2 常用集成算法
1.2.1 Bagging
Bagging集成算法也称为自举聚合(Bootstrap Aggregating)。
在此算法中,每个基本模型都是基于不同数据子集进行训练的。每次训练时,从总训练数据中随机抽取一定比例的数据样本,作为当前模型的训练集。
这样做的好处是可以从不同角度进行训练,减少模型的过拟合风险。
对于多个模型预测出的多个结果,Bagging算法对回归任务进行平均或加权平均,对分类任务进行投票,最后得出结果。
流程就是:
接下来用python实现各流程。
①、②:
import pandas as pd
# 根据数量进行循环
for i in range(num_estimators):
# 随机选择数据
sample = data.sample(frac=sample_ratio, replace=True)
# 获取特征和结果
features = sample.drop(target_variable, axis=1)
target = sample[target_variable]
③:
# 使用随机森林作为基本模型
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(features, target)
④:
# 将预测结果添加到predictions DataFrame中
prediction = model.predict(data.drop(target_variable, axis=1))
predictions[i] = prediction
⑤:
# 对每个样本的预测结果进行投票,选择最常见的类别作为最终预测结果
final_predictions = predictions.mode(axis=1)[0]
完整代码:
import pandas as pd from sklearn.ensemble import RandomForestClassifier def bagging_ensemble(data, target_variable, num_estimators, sample_ratio): # 用于存储基本模型的预测结果 predictions = pd.DataFrame() # 根据数量进行循环 for i in range(num_estimators): # 随机选择数据 sample = data.sample(frac=sample_ratio, replace=True) # 获取特征和结果 features = sample.drop(target_variable, axis=1) target = sample[target_variable] # 使用随机森林作为基本模型 model = RandomForestClassifier() model.fit(features, target) # 将预测结果添加到predictions DataFrame中 prediction = model.predict(data.drop(target_variable, axis=1)) predictions[i] = prediction # 对每个样本的预测结果进行投票,选择最常见的类别作为最终预测结果 final_predictions = predictions.mode(axis=1)[0] return final_predictions# 读取数据 data = pd.read_csv('data.csv') # 调用方法进行集成学习 target_variable = 'result' num_estimators = 10 sample_ratio = 0.8 predictions = bagging_ensemble(data, target_variable, num_estimators, sample_ratio) # 打印预测结果 print(predictions)
1.2.2 Boosting
Boosting算法的核心思想是通过迭代的方式,每次迭代都调整样本的权重或分布,使得在下一次迭代中,分类器能够更关注被错误分类的样本,从而提高整体分类准确性。
1.2.2.1 AdaBoost
算法步骤如下:
接下来我们尝试使用sklearn库实现AdaBoost。
使用AdaBoost算法需要以下步骤:
- 导入所需的库和数据集:
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = pd.read_csv("data.csv")
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
- 创建AdaBoost分类器:
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1),
n_estimators=200,
algorithm="SAMME.R",
learning_rate=0.5,
random_state=42
)
- 使用训练数据拟合分类器:
ada_clf.fit(X_train, y_train)
- 使用分类器进行预测:
y_pred = ada_clf.predict(X_test)
- 计算准确率:
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
其中,DecisionTreeClassifier(max_depth=1)表示基础分类器,n_estimators表示基础分类器的数量,algorithm表示使用的算法,learning_rate表示学习率。最后,通过计算准确率来评估模型的性能。
完整代码:
# 导入所需的库和数据集 import numpy as np import pandas as pd from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import AdaBoostClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score data = pd.read_csv("data.csv") X = data.iloc[:, :-1] y = data.iloc[:, -1] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 创建AdaBoost分类器 ada_clf = AdaBoostClassifier( DecisionTreeClassifier(max_depth=1), n_estimators=200, algorithm="SAMME.R", learning_rate=0.5, random_state=42 ) # 使用训练数据拟合分类器 ada_clf.fit(X_train, y_train) # 使用分类器进行预测 y_pred = ada_clf.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, y_pred) print("Accuracy:", accuracy)
1.2.2.2 GBDT
GBDT(Gradient Boosting Decision Tree)也是一种基于决策树的机器学习算法。GBDT算法通过迭代训练多个弱分类器,使用梯度下降来优化损失函数,最终得到一个强分类器。
GBDT算法的核心思想是在模型训练的过程中不断迭代地学习错误,每一次迭代都会训练一个新的决策树模型,该模型的目的是使得前面所有模型预测错误的样本得到更好的预测结果。因此,GBDT算法可以有效地处理非线性问题和高维数据集,适用于分类和回归任务。
GBDT算法的优点包括:
-
高精度:GBDT算法在大规模数据、非线性问题和高维数据集上的表现非常出色,可以取得很高的精度。
-
鲁棒性:GBDT算法具有很强的鲁棒性,在数据缺失、异常值等情况下能够保持较好的性能。
-
特征选择:GBDT算法可以选择对预测效果最佳的特征,提高模型的泛化能力。
-
可解释性:由于GBDT算法采用决策树模型,因此可以输出变量的重要性,方便模型解释和特征工程。
GBDT算法的缺点包括:
-
训练时间长:GBDT算法需要多次迭代训练,因此训练时间较长。
-
容易过拟合:由于GBDT算法采用的是Boosting思想,容易出现过拟合问题。为避免过拟合问题,需要调节模型参数和控制模型复杂度。
Python中实现GBDT算法可以使用sklearn库中的GradientBoostingRegressor和GradientBoostingClassifier模块。以下是一个简单的示例:
from sklearn.ensemble import GradientBoostingRegressor, GradientBoostingClassifier
# 加载数据集
X_train, y_train = ...
X_test, y_test = ...
# 创建GBDT模型
gbdt = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3)
# 训练模型
gbdt.fit(X_train, y_train)
# 预测
y_pred = gbdt.predict(X_test)
# 计算准确率或均方误差等指标
score = gbdt.score(X_test, y_test)
其中,GradientBoostingRegressor用于回归任务,GradientBoostingClassifier用于分类任务。参数n_estimators表示迭代次数,learning_rate表示学习率,max_depth表示决策树的最大深度。
1.2.2.3 XgBoost
XgBoost(eXtreme Gradient Boosting)在Boosting的基础上,在优化算法和提高速度方面做了很多改进。它支持分类、回归和排名任务,并且在各种机器学习竞赛中表现优异。
Python中实现XgBoost算法可以使用xgboost库。以下是一个简单的示例:
import xgboost as xgb
# 加载数据集
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)
# 设置参数
params = {
'booster': 'gbtree', # 树模型
'objective': 'reg:squarederror', # 回归任务
'eta': 0.1, # 学习率
'max_depth': 5, # 树的最大深度
'subsample': 0.8, # 每棵树样本采样比例
'colsample_bytree': 0.8, # 每棵树特征采样比例
'eval_metric': 'rmse' # 评估指标
}
# 训练模型
num_round = 100 # 迭代次数
model = xgb.train(params, dtrain, num_round)
# 预测
y_pred = model.predict(dtest)
# 计算准确率或均方误差等指标
score = model.score(dtest, y_test)
其中,需要将数据集转换为DMatrix格式,设置参数和训练模型的方式与GBDT类似。需要注意的是,XgBoost也是一种集成学习方法,通常需要和其他特征工程、模型选择、模型融合等技术一起使用,才能发挥出最好的效果。
1.2.3 Stacking
Stacking是基于多个模型进行组合预测的。它的基本思想是:将多个不同类型的弱学习器的预测结果作为输入来训练一个强学习器,以产生最终的预测结果。
Stacking算法的大致步骤如下:
Stacking算法是一种高效而且准确的集成学习方法,因为它可以同时融合多个不同的预测模型,从而产生更准确的预测结果。但是,它需要更多的计算成本和时间,同时也需要更多的调整和优化来避免过拟合和欠拟合等问题。
Python实现:
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
# 构造训练数据集
X, y = make_classification(n_samples=1000, n_informative=5, n_classes=2, random_state=1)
n_folds = 5
kf = KFold(n_folds, shuffle=True, random_state=1)
# 定义基分类器
lr = LogisticRegression()
dt = DecisionTreeClassifier()
nb = GaussianNB()
rf = RandomForestClassifier()
# 训练基分类器并得到其预测结果
def get_oof(clf, X_train, y_train, X_test):
oof_train = np.zeros((X_train.shape[0],))
oof_test = np.zeros((X_test.shape[0],))
oof_test_skf = np.empty((n_folds, X_test.shape[0]))
for i, (train_index, test_index) in enumerate(kf.split(X_train)):
kf_X_train = X_train[train_index]
kf_y_train = y_train[train_index]
kf_X_test = X_train[test_index]
clf.fit(kf_X_train, kf_y_train)
oof_train[test_index] = clf.predict(kf_X_test)
oof_test_skf[i, :] = clf.predict(X_test)
oof_test[:] = oof_test_skf.mean(axis=0)
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1)
# 训练多个基分类器并得到其输出结果
lr_oof_train, lr_oof_test = get_oof(lr, X, y, X)
dt_oof_train, dt_oof_test = get_oof(dt, X, y, X)
nb_oof_train, nb_oof_test = get_oof(nb, X, y, X)
rf_oof_train, rf_oof_test = get_oof(rf, X, y, X)
# 将多个基分类器的输出结果作为元特征集,训练元分类器
X_train = np.concatenate((lr_oof_train, dt_oof_train, nb_oof_train, rf_oof_train), axis=1)
X_test = np.concatenate((lr_oof_test, dt_oof_test, nb_oof_test, rf_oof_test), axis=1)
meta_model = LogisticRegression()
meta_model.fit(X_train, y)
# 使用元分类器进行预测
predictions = meta_model.predict(X_test)
二、聚类算法
2.1 概念
聚类算法是一种无监督学习算法,其目标是将一组未标记的数据样本分成多个相似的群组,群组内部的样本相似度高,群组之间的样本差异度也高。
聚类算法根据相似性度量在数据集中找到相似的数据点,并将其分配到不同的簇中,簇内数据点之间相似度高,簇与簇之间的相似度低。
聚类算法的一般流程如下:
- 随机选择K个簇心(簇心是聚类的中心点)。
- 计算每个样本与K个簇心之间的距离,并将样本分配到距离最近的簇。
- 重新计算每个簇的中心点。
- 重复步骤2和3直到收敛,即簇不再发生变化。
聚类算法在各种领域广泛应用,例如文本聚类、图像分割、市场营销、医学、生物信息学等。
2.2 常用聚类算法
常用的聚类算法包括以下几种:
-
K-means算法:是最常用和最经典的聚类算法之一。它以欧几里得距离作为相似性度量,将数据样本分成K个簇。
-
层次聚类算法:该算法通过计算样本之间的距离将数据点不断合并成越来越大的簇,最终形成一棵层次结构。
-
DBSCAN算法:该算法通过局部密度来确定样本是否属于同一个簇,可以有效地处理噪声和离群值。
-
AP聚类算法:该算法通过簇内数据点之间的传递消息来确定簇的数量和簇心位置,具有很好的稳健性和鲁棒性。
-
高斯混合模型聚类算法:该算法将每个簇看作一个高斯分布,通过最大化似然函数来确定簇的数量,具有良好的灵活性和可解释性。
以上算法各有优缺点,在不同应用场景下选取合适的算法可以获得更好的聚类效果。
2.2.1 K-means
K-means算法是一种常见且经典的聚类算法,它将数据样本分成K个簇,并且每个簇的中心被称为簇心。该算法的基本步骤如下:
-
随机选择K个中心点作为簇心,可以选择样本中的K个点或者通过其他方法选取。
-
将每个样本点分配到最近的簇心所在的簇中。
-
更新每个簇的簇心,计算该簇内所有样本点的平均值并将其作为新簇心。
-
重复步骤2和3,直到所有样本点的簇分配不再变化或达到最大迭代次数。
K-means算法需要选择合适的K值,通常采用肘部法则选择最佳的K值。肘部法则是指在不同的K值下,计算聚类的平均距离平方和(SSE),选择一个SSE急剧下降的点作为最佳的K值。
K-means算法的优点包括简单、易于实现、计算效率高,但其缺点也很明显,如需要预先确定簇的数量、对初始点的选择敏感,容易陷入局部最优解等。
Python可以简单的使用sklearn库实现此算法。
from sklearn.cluster import KMeans
import numpy as np
# 构造样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 设置簇数K为2
kmeans = KMeans(n_clusters=2)
# 训练模型,预测簇分配
kmeans.fit(X)
labels = kmeans.predict(X)
# 输出结果
print("样本数据:\n", X)
print("簇分配:\n", labels)
print("簇心:\n", kmeans.cluster_centers_)
样本数据:
[[1 2]
[1 4]
[1 0]
[4 2]
[4 4]
[4 0]]
簇分配:
[0 0 0 1 1 1]
簇心:
[[ 1. 2. ]
[ 4. 2. ]]
2.2.2 层次聚类
层次聚类算法(Hierarchical Clustering)是一种基于树形结构的聚类方法,它的主要思想是不断将相似的对象合并成为更大的簇,直到所有对象都被合并到同一个簇中或达到某个预设的阈值。
层次聚类算法有两种不同的方法:自底向上的聚合(Agglomerative Clustering)和自顶向下的分裂(Divisive Clustering)。
自底向上的聚合是一种自下而上的聚类方法,将每个样本数据都置为一个初始簇,然后重复以下步骤直至达到停止条件:
- 计算两个最近的簇之间的距离(可以使用不同的距离度量方式)
- 合并两个最近的簇为一个新的簇
- 计算新的簇与所有旧簇(或新簇)之间的距离
自顶向下的分裂是一种自上而下的聚类方法,将所有样本数据都置为一个初始簇,然后重复以下步骤直至达到停止条件:
- 计算当前簇中样本的方差
- 选取方差最大的簇进行分裂,将其分为两个新的簇
- 递归地对新的两个簇进行2步骤操作
Python中,可以使用scikit-learn库中的AgglomerativeClustering类来实现自底向上的聚合层次聚类算法,以下是一个简单的示例代码:
from sklearn.cluster import AgglomerativeClustering
import numpy as np
# 构造样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 设置簇数K为2
agg_clustering = AgglomerativeClustering(n_clusters=2)
# 训练模型,预测簇分配
labels = agg_clustering.fit_predict(X)
# 输出结果
print("样本数据:\n", X)
print("簇分配:\n", labels)
其中,AgglomerativeClustering类的n_clusters参数指定簇数,fit_predict方法用于训练模型并预测簇分配。输出结果显示,所有的样本数据都被正确的分配到了两个簇中。
2.2.3 DBSCAN算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法是一种基于密度的聚类算法,主要用于发现任意形状的密度相连簇集,可以有效地处理噪声和局部密度变化的数据。
DBSCAN算法的核心思想是给定一个密度阈值eps和一个最小包含点数minPts,将样本分为核心点、边界点和噪声点三类,具体步骤如下:
- 随机选取一个未访问的样本点p
- 判断p是否是核心点(周围半径为eps内至少包含minPts个样本点)
- 如果p是核心点,则将其周围eps半径内的所有样本点加入一个新的簇中,并且将这些样本点标记为已访问
- 如果p不是核心点,则标记为噪声点并标记为已访问
- 重复以上步骤,直到所有样本点都被访问
Python中,可以使用scikit-learn库中的DBSCAN类来实现DBSCAN算法,以下是一个简单的示例代码:
from sklearn.cluster import DBSCAN
import numpy as np
# 构造样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 设置密度阈值eps为1,最小包含点数minPts为2
dbscan = DBSCAN(eps=1, min_samples=2)
# 训练模型,预测簇分配
labels = dbscan.fit_predict(X)
# 输出结果
print("样本数据:\n", X)
print("簇分配:\n", labels)
其中,DBSCAN类的eps参数指定密度阈值,min_samples参数指定最小包含点数,fit_predict方法用于训练模型并预测簇分配。输出结果显示,所有的样本数据都被正确的分配到了两个簇中。值得注意的是,-1表示噪声点。
2.2.4 AP聚类算法
AP聚类算法(Affinity Propagation clustering algorithm)是一种基于"消息传递"的聚类算法,它能够有效地自动划分聚类中心和样本点,并且不需要事先指定聚类数量。AP聚类算法的核心思想是利用样本点之间的相似度信息来进行聚类,通过传递消息的方式不断优化聚类中心和样本点的划分。
具体地,AP聚类算法的过程如下:
- 计算样本点之间的相似度矩阵S
- 初始化两个矩阵R和A,其中R[i, k]表示样本点i选择样本点k作为其聚类中心的相对适合度,A[i, k]表示样本点i将样本点k作为聚类中心的相对适合度调整值
- 通过迭代更新矩阵R和A来不断优化聚类中心和样本点的划分,直到满足停止准则(例如收敛或达到最大迭代次数)
- 最后,根据聚类中心和样本点的划分结果来进行聚类
Python中,可以使用scikit-learn库中的AffinityPropagation类来实现AP聚类算法,以下是一个简单的示例代码:
from sklearn.cluster import AffinityPropagation
import numpy as np
# 构造样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 设置阻尼因子damping为0.5
ap = AffinityPropagation(damping=0.5)
# 训练模型,预测簇分配
labels = ap.fit_predict(X)
# 输出结果
print("样本数据:\n", X)
print("簇分配:\n", labels)
其中,AffinityPropagation类的damping参数指定阻尼因子,fit_predict方法用于训练模型并预测簇分配。输出结果显示,所有的样本数据都被正确地分配到了两个簇中。
2.2.5 高斯混合模型聚类算法
高斯混合模型聚类算法(Gaussian Mixture Model clustering algorithm)是一种基于概率模型的聚类算法,它假设样本数据是由多个高斯分布混合而成的,并通过最大化似然函数来估计模型参数和聚类结果。高斯混合模型聚类算法能够适用于各种形状、大小和密度的聚类,并且可以进行密度估计和异常检测。
具体地,高斯混合模型聚类算法的过程如下:
- 随机初始化高斯混合模型的参数(包括每个高斯分布的均值、方差和混合系数)
- 根据当前的高斯混合模型参数,计算样本数据属于每个高斯分布的概率,并根据概率大小分配样本数据到对应的簇中
- 基于当前的样本簇分配,更新高斯混合模型的参数,最大化似然函数
- 重复步骤2和步骤3,直到满足停止准则(例如收敛或达到最大迭代次数)
- 最后,根据样本簇分配结果来进行聚类
Python中,可以使用scikit-learn库中的GaussianMixture类来实现高斯混合模型聚类算法,以下是一个简单的示例代码:
from sklearn.mixture import GaussianMixture
import numpy as np
# 构造样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 设置高斯分布数量为2
gmm = GaussianMixture(n_components=2)
# 训练模型,预测簇分配
labels = gmm.fit_predict(X)
# 输出结果
print("样本数据:\n", X)
print("簇分配:\n", labels)
其中,GaussianMixture类的n_components参数指定高斯分布数量,fit_predict方法用于训练模型并预测簇分配。输出结果显示,所有的样本数据都被正确地分配到了两个簇中。
这一期我写了3天,很高兴你能看到这里,给个免费的赞可以吗?谢谢!