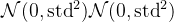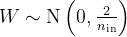24.11.26 神经网络参数初始化

神经网络

感知神经网络

神经网络（Neural Networks）是一种模拟人脑神经元网络结构的计算模型，用于处理复杂的模式识别、分类和预测等任务

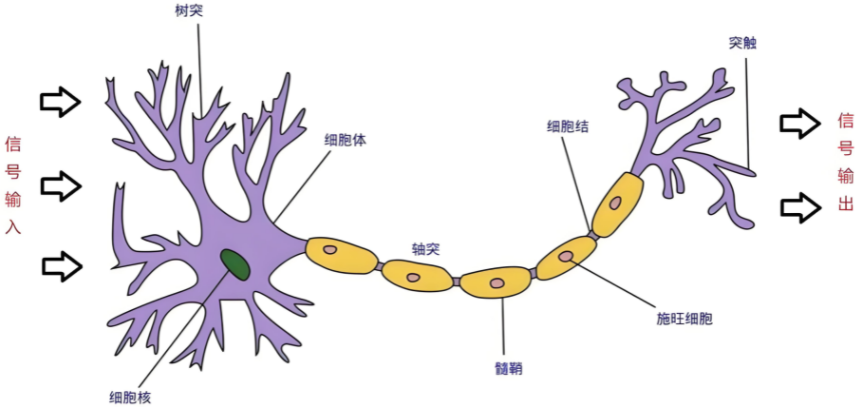
生物学：

人脑可以看做是一个生物神经网络，由众多的神经元连接而成

树突：从其他神经元接收信息的分支
细胞核：处理从树突接收到的信息
轴突：被神经元用来传递信息的生物电缆
突触：轴突和其他神经元树突之间的连接

人脑神经元处理信息的过程：

多个信号到达树突，然后整合到细胞体的细胞核中
当积累的信号超过某个阈值，细胞就会被激活
产生一个输出信号，由轴突传递。

神经网络由多个互相连接的节点（即人工神经元）组成。

人工神经元

人工神经元(Artificial Neuron)是神经网络的基本构建单元，模仿了生物神经元的工作原理。其核心功能是接收输入信号，经过加权求和和非线性激活函数处理后，输出结果。

构建人工神经元

人工神经元接受多个输入信息，对它们进行加权求和，再经过激活函数处理，最后将这个结果输出。

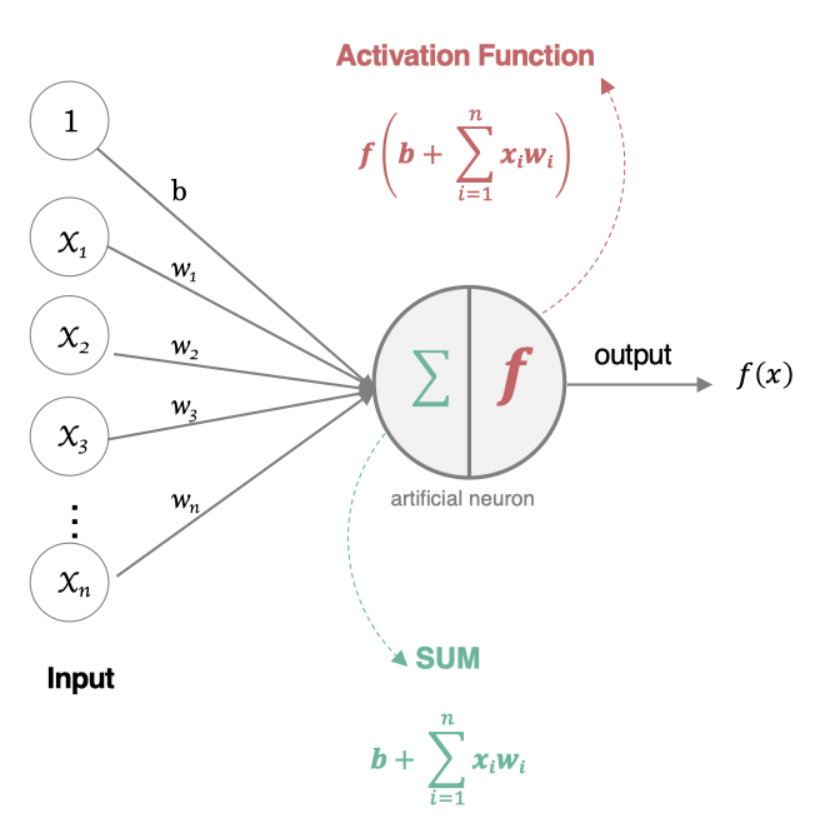
组成部分

输入（Inputs）: 代表输入数据，通常用向量表示，每个输入值对应一个权重。
权重（Weights）: 每个输入数据都有一个权重，表示该输入对最终结果的重要性。
偏置（Bias）: 一个额外的可调参数，作用类似于线性方程中的截距，帮助调整模型的输出。
加权求和: 神经元将输入乘以对应的权重后求和，再加上偏置。
激活函数（Activation Function）: 用于将加权求和后的结果转换为输出结果，引入非线性特性，使神经网络能够处理复杂的任务。常见的激活函数有Sigmoid、ReLU（Rectified Linear Unit）、Tanh等。

数学表示

如果有 n 个输入 x_1, x_2, \ldots, x_n，权重分别为 w_1, w_2, \ldots, w_n，偏置为 b，则神经元的输出 y 表示为：

$z=\sum_{i=1}^nw_i\cdot x_i+b \\ y=\sigma(z)$

其中，\sigma(z) 是激活函数。

对比生物神经元

人工神经元和生物神经元对比如下表：

生物神经元	人工神经元
细胞核	节点 (加权求和 + 激活函数)
树突	输入
轴突	带权重的连接
突触	输出

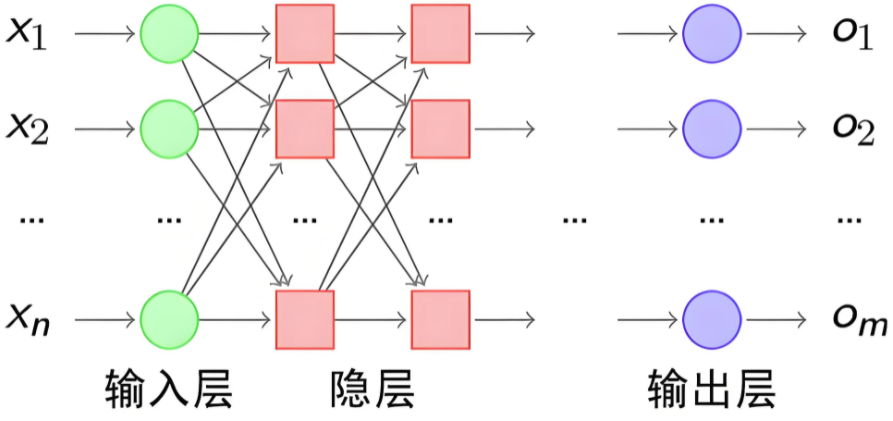
深入神经网络

神经网络是由大量人工神经元按层次结构连接而成的计算模型。每一层神经元的输出作为下一层的输入，最终得到网络的输出。

基本结构

神经网络有下面三个基础层（Layer）构建而成：

输入层（Input）: 神经网络的第一层，负责接收外部数据，不进行计算。
隐藏层（Hidden）: 位于输入层和输出层之间，进行特征提取和转换。隐藏层一般有多层，每一层有多个神经元。
输出层（Output）: 网络的最后一层，产生最终的预测结果或分类结果

网络构建

我们使用多个神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个权重，经典如下：

注意：同一层的各个神经元之间是没有连接的。

全连接神经网络

全连接（Fully Connected，FC）神经网络是前馈神经网络的一种，每一层的神经元与上一层的所有神经元全连接，常用于图像分类、文本分类等任务。

特点

全连接层: 层与层之间的每个神经元都与前一层的所有神经元相连。
权重数量: 由于全连接的特点，权重数量较大，容易导致计算量大、模型复杂度高。
学习能力: 能够学习输入数据的全局特征，但对于高维数据却不擅长捕捉局部特征（如图像就需要CNN）。

计算步骤

数据传递: 输入数据经过每一层的计算，逐层传递到输出层。
激活函数: 每一层的输出通过激活函数处理。
损失计算: 在输出层计算预测值与真实值之间的差距，即损失函数值。
反向传播（Back Propagation）: 通过反向传播算法计算损失函数对每个权重的梯度，并更新权重以最小化损失。

参数初始化

神经网络的参数初始化是训练深度学习模型的关键步骤之一。初始化参数（通常是权重和偏置）会对模型的训练速度、收敛性以及最终的性能产生重要影响

固定值初始化

固定值初始化是指在神经网络训练开始时，将所有权重或偏置初始化为一个特定的常数值。这种初始化方法虽然简单，但在实际深度学习应用中通常并不推荐。

全零初始化

将神经网络中的所有权重参数初始化为0。

方法：将所有权重初始化为零。

缺点：导致对称性破坏，每个神经元在每一层中都会执行相同的计算，模型无法学习。

应用场景：通常不用来初始化权重，但可以用来初始化偏置。

全1初始化

全1初始化会导致网络中每个神经元接收到相同的输入信号，进而输出相同的值，这就无法进行学习和收敛。所以全1初始化只是一个理论上的初始化方法，但在实际神经网络的训练中并不适用。

任意常数初始化

将所有参数初始化为某个非零的常数（如 0.1，-1 等）。虽然不同于全0和全1，但这种方法依然不能避免对称性破坏的问题。

随机初始化

方法：将权重初始化为随机的小值，通常从正态分布或均匀分布中采样。

应用场景：这是最基本的初始化方法，通过随机初始化避免对称性破坏。

Xavier 初始化

也叫做Glorot初始化。

方法：根据输入和输出神经元的数量来选择权重的初始值。权重从以下分布中采样：

$W\sim\mathrm{U}\left(-\frac{\sqrt{6}}{\sqrt{n_\mathrm{in}+n_\mathrm{out}}},\frac{\sqrt{6}}{\sqrt{n_\mathrm{in}+n_\mathrm{out}}}\right)$

或者

$W\sim\mathrm{N}\left(0,\frac{2}{n_\mathrm{in}+n_\mathrm{out}}\right)$

$\mathcal{N}(0, \text{std}^2)\mathcal{N}(0, \text{std}^2)$

其中 n_{\text{in}} 是当前层的输入神经元数量，n_{\text{out}}是输出神经元数量。

优点：平衡了输入和输出的方差，适合Sigmoid 和 Tanh 激活函数。

应用场景：常用于浅层网络或使用Sigmoid 、Tanh 激活函数的网络。

He初始化

也叫kaiming 初始化。

方法：专门为 ReLU 激活函数设计。权重从以下分布中采样：

$W\sim\mathrm{N}\left(0,\frac{2}{n_\mathrm{in}}\right)$

其中 n_{\text{in}} 是当前层的输入神经元数量。

优点：适用于ReLU 和 Leaky ReLU 激活函数。

应用场景：深度网络，尤其是使用 ReLU 激活函数时。

总结

在使用Torch构建网络模型时，每个网络层的参数都有默认的初始化方法，同时还可以通过以上方法来对网络参数进行初始化。

代码演示:

import torch


def t1():
    # 任意常数初始化
    model = torch.nn.Linear(4, 1)
    print(model.weight)
    model.weight.data.fill_(0)
    print(model.weight)


def t2():
    # 全1填充初始化
    model = torch.nn.Linear(4, 1)
    torch.nn.init.ones_(model.weight)
    print(model.weight)


def t3():
    # 任意常数初始化
    model = torch.nn.Linear(4, 1)
    torch.nn.init.constant_(model.weight, 0.63)
    print(model.weight)


def t6():
    # Xavier初始化：正态分布
    linear = torch.nn.Linear(in_features=6, out_features=4)
    torch.nn.init.xavier_normal_(linear.weight)
    print(linear.weight)

    # Xavier初始化：均匀分布
    linear = torch.nn.Linear(in_features=6, out_features=4)
    torch.nn.init.xavier_uniform_(linear.weight)
    print(linear.weight)


def t7():
    # He初始化 均匀分布
    model = torch.nn.Linear(6, 8)
    torch.nn.init.kaiming_uniform_(model.weight)
    print(model.weight)
    # He初始化 正态分布
    model2 = torch.nn.Linear(6, 8)
    torch.nn.init.kaiming_normal_(model2.weight)
    print(model2.weight)


if __name__ == '__main__':
    t1()
    t2()
    t3()
    t6()
    t7()

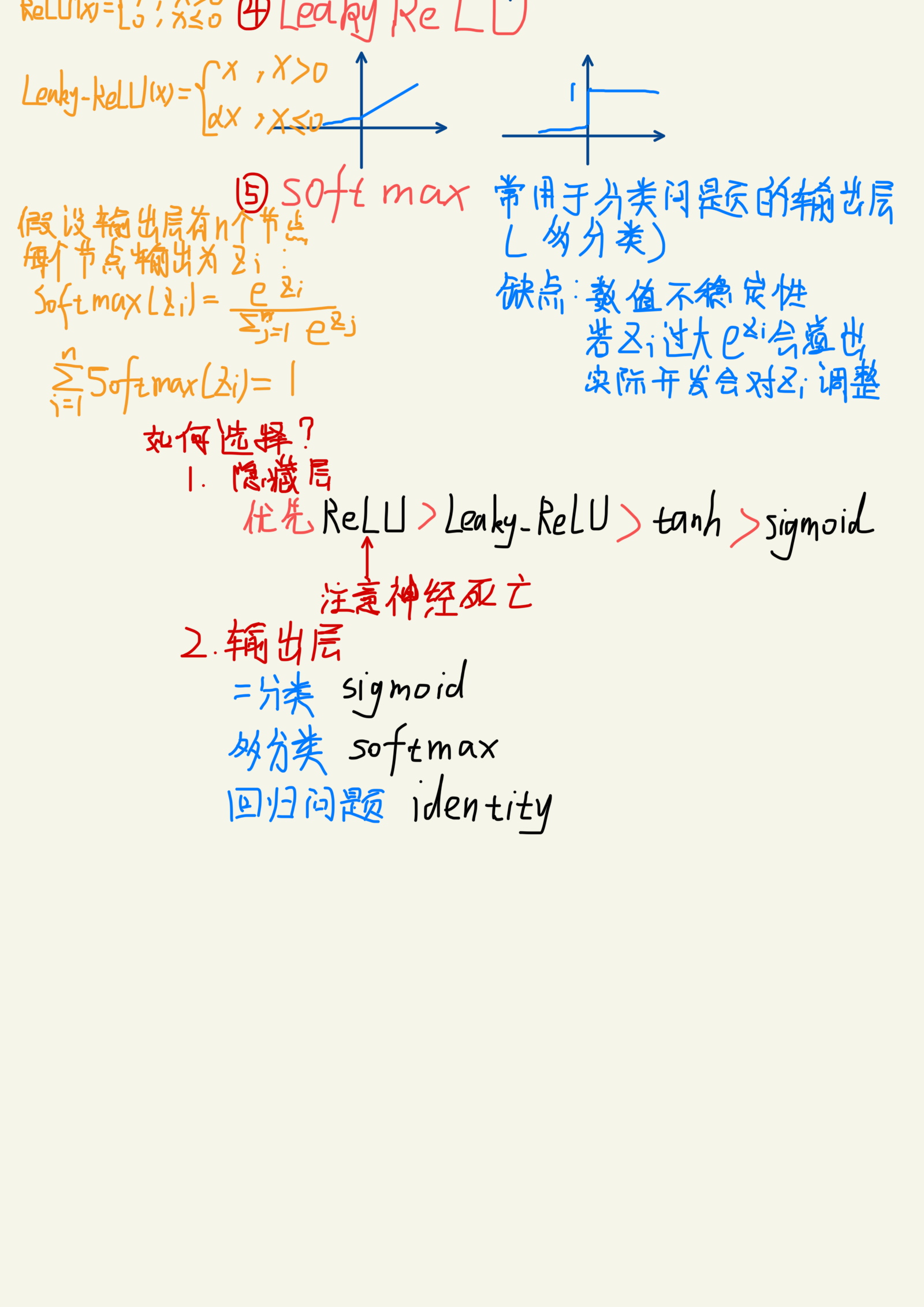
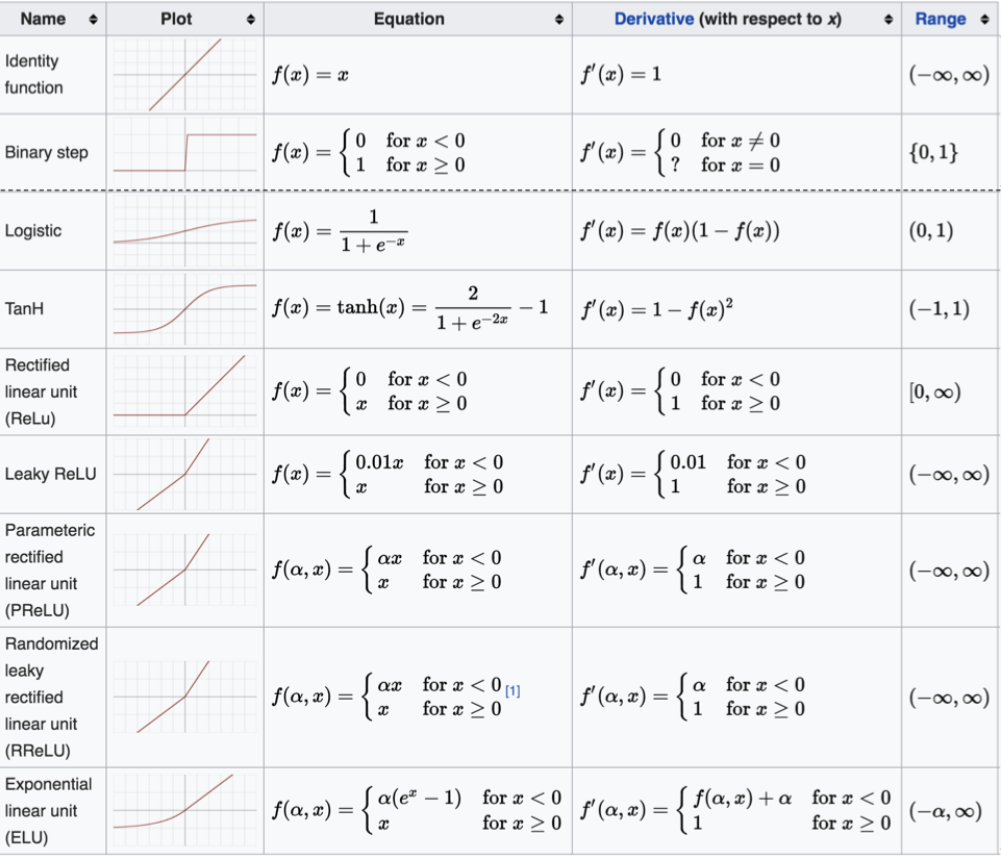
激活函数

激活函数的作用是在隐藏层引入非线性，使得神经网络能够学习和表示复杂的函数关系，使网络具备非线性能力，增强其表达能力。

基础概念

非线性理解

如果在隐藏层不使用激活函数，那么整个神经网络会表现为一个线性模型。我们可以通过数学推导来展示这一点。

假设：

神经网络有L 层，每层的输出为 $\mathbf{a}^{(l)}$ 。
每层的权重矩阵为 $\mathbf{W}^{(l)}$ ，偏置向量为 $\mathbf{b}^{(l)}$ 。
输入数据为 $\mathbf{x}$ ，输出为 $\mathbf{a}^{(L)}$ 。

一层网络的情况

对于单层网络（输入层到输出层），如果没有激活函数，输出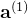 $\mathbf{a}^{(1)}$ 可以表示为： $\mathbf{a}^{(1)} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}$

两层网络的情况

假设我们有两层网络，且每层都没有激活函数，则：

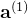
第一层的输出： $\mathbf{a}^{(1)} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}$
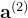
第二层的输出： $\mathbf{a}^{(2)} = \mathbf{W}^{(2)} \mathbf{a}^{(1)} + \mathbf{b}^{(2)}$

将 $\mathbf{a}^{(1)}$ 代入到 $\mathbf{a}^{(2)}$ 中，可以得到：

$\mathbf{a}^{(2)} = \mathbf{W}^{(2)} (\mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}) + \mathbf{b}^{(2)}$

$\mathbf{a}^{(2)} = \mathbf{W}^{(2)} \mathbf{W}^{(1)} \mathbf{x} + \mathbf{W}^{(2)} \mathbf{b}^{(1)} + \mathbf{b}^{(2)}$

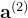
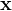
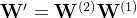
我们可以看到，输出 $\mathbf{a}^{(2)}$ 是输入 $\mathbf{x}$ 的线性变换，因为： $\mathbf{a}^{(2)} = \mathbf{W}' \mathbf{x} + \mathbf{b}'$ 其中 $\mathbf{W}' = \mathbf{W}^{(2)} \mathbf{W}^{(1)}$ ， $\mathbf{b}' = \mathbf{W}^{(2)} \mathbf{b}^{(1)} + \mathbf{b}^{(2)}$ 。

多层网络的情况

如果有L层，每层都没有激活函数，则第l层的输出为： $\mathbf{a}^{(l)} = \mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}$

通过递归代入，可以得到：
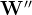
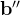
$\mathbf{a}^{(L)} = \mathbf{W}^{(L)} \mathbf{W}^{(L-1)} \cdots \mathbf{W}^{(1)} \mathbf{x} + \mathbf{W}^{(L)} \mathbf{W}^{(L-1)} \cdots \mathbf{W}^{(2)} \mathbf{b}^{(1)} + \mathbf{W}^{(L)} \mathbf{W}^{(L-1)} \cdots \mathbf{W}^{(3)} \mathbf{b}^{(2)} + \cdots + \mathbf{b}^{(L)}$

表达式可简化为：

$\mathbf{a}^{(L)} = \mathbf{W}'' \mathbf{x} + \mathbf{b}''$

其中， $\mathbf{W}''$ 是所有权重矩阵的乘积， $\mathbf{b}''$ 是所有偏置项的线性组合。

如此可以看得出来，无论网络多少层，意味着：

整个网络就是线性模型，无法捕捉数据中的非线性关系。

激活函数是引入非线性特性、使神经网络能够处理复杂问题的关键。

1.2 非线性可视化

我们可以通过可视化的方式去理解非线性的拟合能力:：A Neural Network Playgroundhttps://playground.tensorflow.org/

常见激活函数

sigmoid

import matplotlib.pyplot as plt
import torch


def t001():
    # 一行两列的图像绘制
    _, ax = plt.subplots(1, 2)
    # 绘制函数图像
    x = torch.linspace(-10, 10, 100)
    y = torch.sigmoid(x)
    # 网格
    ax[0].grid(True)
    ax[0].set_title("sigmoid")
    ax[0].set_xlabel("x")
    ax[0].set_ylabel("y")
    # 绘制
    ax[0].plot(x, y)

    # 绘制sigmoid导数曲线图
    x = torch.linspace(-10, 10, 100, requires_grad=True)
    # 自动求导
    torch.sigmoid(x).sum().backward()
    ax[1].grid(True)
    ax[1].set_title("sigmoid's plot", color="red")
    ax[1].set_xlabel("x")
    ax[1].set_ylabel("y")
    # 用自动求导的结果绘制曲线图
    ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())

    plt.show()


if __name__ == '__main__':
    t001()

tanh

import matplotlib.pyplot as plt
import torch


def t001():
    # 一行两列的图像绘制
    _, ax = plt.subplots(1, 2)
    # 绘制函数图像
    x = torch.linspace(-10, 10, 100)
    y = torch.tanh(x)
    # 网格
    ax[0].grid(True)
    ax[0].set_title("tanh")
    ax[0].set_xlabel("x")
    ax[0].set_ylabel("y")
    # 绘制
    ax[0].plot(x, y)

    # 绘制sigmoid导数曲线图
    x = torch.linspace(-10, 10, 100, requires_grad=True)
    # 自动求导
    torch.tanh(x).sum().backward()
    ax[1].grid(True)
    ax[1].set_title("tanh plot", color="red")
    ax[1].set_xlabel("x")
    ax[1].set_ylabel("y")
    # 用自动求导的结果绘制曲线图
    ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())

    plt.show()


if __name__ == '__main__':
    t001()

ReLU

import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F

def t001():
    # 一行两列的图像绘制
    _, ax = plt.subplots(1, 2)
    # 绘制函数图像
    x = torch.linspace(-10, 10, 100)
    y = F.relu(x)
    # 网格
    ax[0].grid(True)
    ax[0].set_title("ReLU")
    ax[0].set_xlabel("x")
    ax[0].set_ylabel("y")
    # 绘制
    ax[0].plot(x, y)

    # 绘制sigmoid导数曲线图
    x = torch.linspace(-10, 10, 100, requires_grad=True)
    # 自动求导
    F.relu(x).sum().backward()
    ax[1].grid(True)
    ax[1].set_title("ReLU plot", color="red")
    ax[1].set_xlabel("x")
    ax[1].set_ylabel("y")
    # 用自动求导的结果绘制曲线图
    ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())

    plt.show()


if __name__ == '__main__':
    t001()

LeakyReLU

import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F

def t001():
    # 一行两列的图像绘制
    _, ax = plt.subplots(1, 2)
    # 绘制函数图像
    x = torch.linspace(-10, 10, 100)
    y = F.leaky_relu(x)
    # 网格
    ax[0].grid(True)
    ax[0].set_title("leaky_ReLU")
    ax[0].set_xlabel("x")
    ax[0].set_ylabel("y")
    # 绘制
    ax[0].plot(x, y)

    # 绘制sigmoid导数曲线图
    x = torch.linspace(-10, 10, 100, requires_grad=True)
    # 自动求导
    F.leaky_relu(x).sum().backward()
    ax[1].grid(True)
    ax[1].set_title("leaky_ReLU plot", color="red")
    ax[1].set_xlabel("x")
    ax[1].set_ylabel("y")
    # 用自动求导的结果绘制曲线图
    ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())

    plt.show()


if __name__ == '__main__':
    t001()