贝叶斯学习
一般情形下的贝叶斯估计(总结)
基本假设:
-
密度 p ( x ∣ θ ) p(\mathbf{x}\vert \theta) p(x∣θ)的形式已知,但参数向量的值未知。
-
关于 θ \theta θ的初始知识包含在已知的先验密度 p ( θ ) p(\theta) p(θ)中。
-
关于 θ \theta θ的其余知识包含在根据未知概率密度 p ( x ) p(\mathbf{x}) p(x)独立抽取的 n n n个样本 x 1 , x 2 , ⋯ , x n x_{1},x_{2},\cdots,x_{n} x1,x2,⋯,xn的集合 D D D中。
-
基本问题:计算关于参数 θ \theta θ的后验密度 p ( θ ∣ D ) p(\theta\vert D) p(θ∣D)和关于数据的后验密度 p ( x ∣ D ) p(\mathbf{x}\vert D) p(x∣D)。
p ( θ ∣ D ) = p ( D ∣ θ ) p ( θ ) ∫ p ( D ∣ θ ) p ( θ ) d θ , p ( D ∣ θ ) = P ( x 1 , x 2 , ⋯ , x n ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) p ( x ∣ D ) = ∫ θ p ( x ∣ θ ) p ( θ ∣ D ) d θ p(\theta\vert D)=\frac{p(D\vert \theta)p(\theta)}{\int p(D\vert \theta)p(\theta)d\theta},\quad p(D\vert \theta)=P(x_{1},x_{2},\cdots,x_{n}\vert \theta)=\prod_{i = 1}^{n}p(x_{i}\vert \theta)\\ p(\mathbf{x}\vert D)=\int_{\theta}p(\mathbf{x}\vert \theta)p(\theta\vert D)d\theta p(θ∣D)=∫p(D∣θ)p(θ)dθp(D∣θ)p(θ),p(D∣θ)=P(x1,x2,⋯,xn∣θ)=i=1∏np(xi∣θ)p(x∣D)=∫θp(x∣θ)p(θ∣D)dθ
**遇到的困难: **
-
除了一些特殊的分布(共轭分布)之外,对于一般情形,积分很难计算:
p ( θ ∣ D ) = p ( D ∣ θ ) p ( θ ) ∫ p ( D ∣ θ ) p ( θ ) d θ , p ( x ∣ θ ) = ∫ θ p ( x ∣ θ ) p ( θ ∣ D ) d θ p(\theta\vert D)=\frac{p(D\vert \theta)p(\theta)}{\int p(D\vert \theta)p(\theta)d\theta},\quad p(\mathbf{x}\vert \theta)=\int_{\theta}p(\mathbf{x}\vert \theta)p(\theta\vert D)d\theta p(θ∣D)=∫p(D∣θ)p(θ)dθp(D∣θ)p(θ),p(x∣θ)=∫θp(x∣θ)p(θ∣D)dθ -
参数先验 p ( θ ) p(\theta) p(θ)怎么选取?对结果有何影响?
p(θ) 的选择对结果有直接影响。先验分布过于强烈可能会导致数据驱动的结果被先验主导,而过于弱的先验分布可能导致计算结果不稳定。
-
给定 D D D,我们真的能通过 p ( x ∣ D ) p(\mathbf{x}\vert D) p(x∣D)将 p ( x ) p(\mathbf{x}) p(x)估计得很好吗?或者说,随着 D D D中样本的增多, p ( x ∣ D ) p(\mathbf{x}\vert D) p(x∣D)收敛于 p ( x ) p(\mathbf{x}) p(x)吗?
根据贝叶斯学习的性质,当数据量 n → ∞ n \to \infty n→∞时,后验分布 p ( θ ∣ D ) p(\theta\vert D) p(θ∣D)会集中在最大似然估计值附近,即: p ( θ ∣ D ) → δ ( θ − θ MLE ) p(\theta\vert D) \to \delta(\theta-\theta_{\text{MLE}}) p(θ∣D)→δ(θ−θMLE)这意味着后验分布的方差会逐渐缩小,预测分布 p(\mathbf{x}∣D)p(\mathbf{x}\vert D) 也会趋近于真实分布。
**贝叶斯学习的迭代计算公式: **
-
记 D n = { x 1 , x 2 , ⋯ , x n } D^{n}=\{x_{1},x_{2},\cdots,x_{n}\} Dn={x1,x2,⋯,xn},由于样本是独立选样,则:
p ( D n ∣ θ ) = p ( x n ∣ θ ) p ( D n − 1 ∣ θ ) = p ( x n ∣ θ ) p ( x n − 1 ∣ θ ) p ( D n − 2 ∣ θ ) = ⋯ p(D^{n}\vert \theta)=p(x_{n}\vert \theta)p(D^{n - 1}\vert \theta)=p(x_{n}\vert \theta)p(x_{n - 1}\vert \theta)p(D^{n - 2}\vert \theta)=\cdots p(Dn∣θ)=p(xn∣θ)p(Dn−1∣θ)=p(xn∣θ)p(xn−1∣θ)p(Dn−2∣θ)=⋯ -
于是有如下迭代公式:
p ( θ ∣ D n ) = p ( D n ∣ θ ) p ( θ ) ∫ p ( D n ∣ θ ) p ( θ ) d θ = p ( x n ∣ θ ) p ( D n − 1 ∣ θ ) p ( θ ) ∫ p ( x n ∣ θ ) p ( D n − 1 ∣ θ ) p ( θ ) d θ = p ( x n ∣ θ ) ∫ p ( x n ∣ θ ) p ( D n − 1 ∣ θ ) p ( θ ) ∫ p ( D n − 1 ∣ θ ) p ( θ ) d θ d θ = p ( x n ∣ θ ) ∫ p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) d θ = p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) ∫ p ( x n ∣ θ ) p ( θ ∣ D n − 1 ) d θ p ( θ ∣ D n − 1 ) = p ( D n − 1 ∣ θ ) p ( θ ) ∫ p ( D n − 1 ∣ θ ) p ( θ ) d θ \begin{align} p(\theta|D^{n})&=\frac{p(D^{n}|\theta)p(\theta)}{\int p(D^{n}|\theta)p(\theta)d\theta}=\frac{p(x_{n}|\theta)p(D^{n - 1}|\theta)p(\theta)}{\int p(x_{n}|\theta)p(D^{n - 1}|\theta)p(\theta)d\theta} \\ &=\frac{p(x_{n}|\theta)}{\int p(x_{n}|\theta)\frac{p(D^{n - 1}|\theta)p(\theta)}{\int p(D^{n - 1}|\theta)p(\theta)d\theta}d\theta}=\frac{p(x_{n}|\theta)}{\int p(x_{n}|\theta)p(\theta|D^{n - 1})d\theta} \\ &=\frac{p(x_{n}|\theta)p(\theta|D^{n - 1})}{\int p(x_{n}|\theta)p(\theta|D^{n - 1})d\theta} \\ p(\theta|D^{n - 1})&=\frac{p(D^{n - 1}|\theta)p(\theta)}{\int p(D^{n - 1}|\theta)p(\theta)d\theta} \end{align} p(θ∣Dn)p(θ∣Dn−1)=∫p(Dn∣θ)p(θ)dθp(Dn∣θ)p(θ)=∫p(xn∣θ)p(Dn−1∣θ)p(θ)dθp(xn∣θ)p(Dn−1∣θ)p(θ)=∫p(xn∣θ)∫p(Dn−1∣θ)p(θ)dθp(Dn−1∣θ)p(θ)dθp(xn∣θ)=∫p(xn∣θ)p(θ∣Dn−1)dθp(xn∣θ)=∫p(xn∣θ)p(θ∣Dn−1)dθp(xn∣θ)p(θ∣Dn−1)=∫p(Dn−1∣θ)p(θ)dθp(Dn−1∣θ)p(θ)
为统一表示,记参数先验分布 p ( θ ) p(\theta) p(θ)为 p ( θ ∣ D 0 ) p(\theta\vert D^{0}) p(θ∣D0),表示没有样本情形下的参数概率密度估计。
记
D
n
=
{
x
1
,
x
2
,
⋯
,
x
n
}
D^{n}=\{x_{1},x_{2},\cdots,x_{n}\}
Dn={x1,x2,⋯,xn},随着样本的增加,可以得到一系列对参数概率密度函数的估计:
p
(
θ
)
,
p
(
θ
∣
x
1
)
,
p
(
θ
∣
x
1
,
x
2
)
,
⋯
,
p
(
θ
∣
x
1
,
x
2
,
⋯
,
x
n
)
,
⋯
p(\theta),p(\theta\vert x_{1}),p(\theta\vert x_{1},x_{2}),\cdots,p(\theta\vert x_{1},x_{2},\cdots,x_{n}),\cdots
p(θ),p(θ∣x1),p(θ∣x1,x2),⋯,p(θ∣x1,x2,⋯,xn),⋯
一般来说,随着样本数目的增加,上述序列函数逐渐尖锐,逐步趋向于以
θ
\theta
θ的真实值为中心的一个尖峰。当样本无穷多时,此时将收敛于一个脉冲函数(参数真值).
例:贝叶斯估计
假设一维随机变量
X
X
X服从
[
0
,
θ
]
[0,\theta]
[0,θ]上的均匀分布:
p
(
x
∣
θ
)
=
U
(
0
,
θ
)
=
{
1
θ
,
0
≤
x
≤
θ
0
,
otherwise
p(\mathbf{x}\vert \theta)=U(0,\theta)=\begin{cases} \frac 1 \theta, & 0\leq \mathbf{x}\leq\theta\\ 0, & \text{otherwise} \end{cases}
p(x∣θ)=U(0,θ)={θ1,0,0≤x≤θotherwise
基于先验知识,我们知道
0
<
θ
<
10
0 < \theta < 10
0<θ<10,并希望利用迭代的贝叶斯方法从样本
{
4
,
7
,
2
,
8
}
\{4,7,2,8\}
{4,7,2,8}中估计参数
θ
\theta
θ。
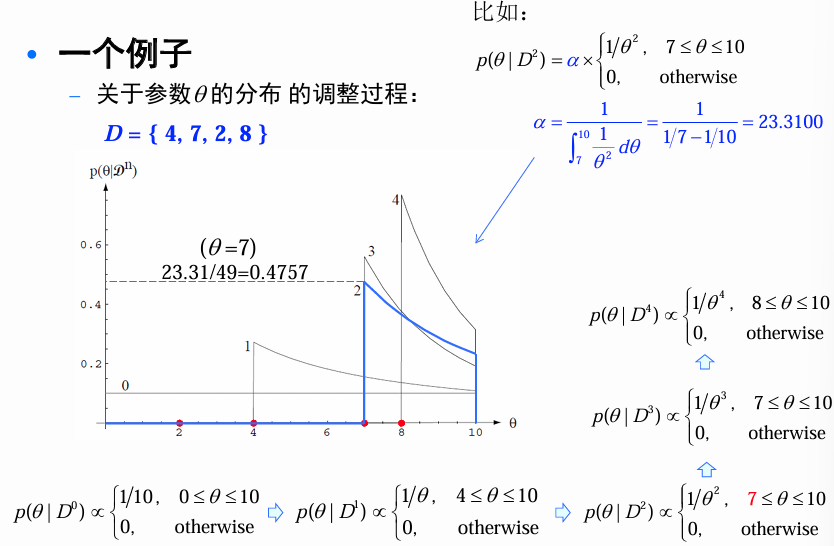
迭代过程
在任何数据到达之前,我们有 p ( θ ∣ D 0 ) = p ( θ ) = U ( 0 , 10 ) p(\theta\vert D^{0}) = p(\theta)=U(0,10) p(θ∣D0)=p(θ)=U(0,10)。
当第一个数据点
x
1
=
4
x_{1}=4
x1=4到达时,则:
p
(
θ
∣
D
1
)
=
p
(
x
1
∣
θ
)
p
(
θ
∣
D
0
)
∫
p
(
x
1
∣
θ
)
p
(
θ
∣
D
0
)
d
θ
=
α
p
(
x
1
∣
θ
)
p
(
θ
∣
D
0
)
=
α
1
θ
1
10
p
(
θ
∣
D
1
)
∝
{
1
/
θ
,
4
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{1})=\frac{p(x_{1}\vert \theta)p(\theta\vert D^{0})}{\int p(x_{1}\vert \theta)p(\theta\vert D^{0})d\theta}=\alpha p(x_{1}\vert \theta)p(\theta\vert D^{0})=\alpha\frac{1}{\theta}\frac{1}{10}\\ p(\theta\vert D^{1})\propto\begin{cases} 1/\theta, & 4\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣D1)=∫p(x1∣θ)p(θ∣D0)dθp(x1∣θ)p(θ∣D0)=αp(x1∣θ)p(θ∣D0)=αθ1101p(θ∣D1)∝{1/θ,0,4≤θ≤10otherwise
其中忽略了归一化。因为
θ
\theta
θ一定要大于等于观测值
x
\mathbf x
x。
当第二个数据点
x
2
=
7
x_{2}=7
x2=7到达时,我们有:
p
(
θ
∣
D
2
)
∝
p
(
x
2
∣
θ
)
p
(
θ
∣
D
1
)
=
1
θ
2
,
p
(
θ
∣
D
2
)
∝
{
1
/
θ
2
,
7
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{2})\propto p(x_{2}\vert \theta)p(\theta\vert D^{1})=\frac{1}{\theta^{2}},\quad p(\theta\vert D^{2})\propto\begin{cases} 1/\theta^{2}, & 7\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣D2)∝p(x2∣θ)p(θ∣D1)=θ21,p(θ∣D2)∝{1/θ2,0,7≤θ≤10otherwise
当第三个数据点
x
3
=
2
x_{3}=2
x3=2到达时,我们有:
p
(
θ
∣
D
3
)
∝
p
(
x
3
∣
θ
)
p
(
θ
∣
D
2
)
=
1
θ
3
,
p
(
θ
∣
D
3
)
∝
{
1
/
θ
3
,
7
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{3})\propto p(x_{3}\vert \theta)p(\theta\vert D^{2})=\frac{1}{\theta^{3}},\quad p(\theta\vert D^{3})\propto\begin{cases} 1/\theta^{3}, & 7\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣D3)∝p(x3∣θ)p(θ∣D2)=θ31,p(θ∣D3)∝{1/θ3,0,7≤θ≤10otherwise
当第四个数据点
x
4
=
8
x_{4}=8
x4=8到达时,我们有:
p
(
θ
∣
D
4
)
∝
p
(
x
4
∣
θ
)
p
(
θ
∣
D
3
)
=
1
θ
4
,
p
(
θ
∣
D
4
)
∝
{
1
/
θ
4
,
8
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{4})\propto p(x_{4}\vert \theta)p(\theta\vert D^{3})=\frac{1}{\theta^{4}},\quad p(\theta\vert D^{4})\propto\begin{cases} 1/\theta^{4}, & 8\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣D4)∝p(x4∣θ)p(θ∣D3)=θ41,p(θ∣D4)∝{1/θ4,0,8≤θ≤10otherwise
当数据点
x
n
x_{n}
xn到达时,我们有:
p
(
θ
∣
D
n
)
∝
p
(
x
n
∣
θ
)
p
(
θ
∣
D
n
−
1
)
=
1
θ
n
,
p
(
θ
∣
D
n
)
∝
{
1
/
θ
n
,
max
{
D
n
}
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{n})\propto p(x_{n}\vert \theta)p(\theta\vert D^{n - 1})=\frac{1}{\theta^{n}},\quad p(\theta\vert D^{n})\propto\begin{cases} 1/\theta^{n}, & \max\{D^{n}\}\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣Dn)∝p(xn∣θ)p(θ∣Dn−1)=θn1,p(θ∣Dn)∝{1/θn,0,max{Dn}≤θ≤10otherwise
关于参数 θ \theta θ的分布的调整过程:
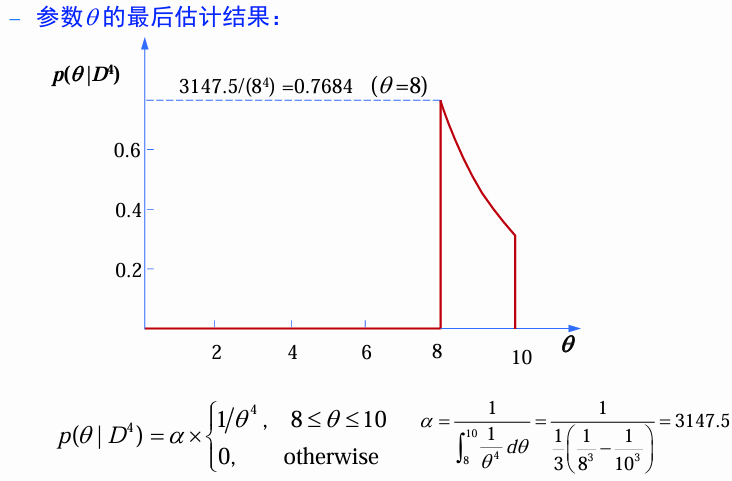
参数 θ \theta θ的最后估计结果:
p
(
θ
∣
D
4
)
=
{
3147.5
/
θ
4
,
8
≤
θ
≤
10
0
,
otherwise
p(\theta\vert D^{4})=\begin{cases} 3147.5/\theta^{4}, & 8\leq\theta\leq10\\ 0, & \text{otherwise} \end{cases}
p(θ∣D4)={3147.5/θ4,0,8≤θ≤10otherwise
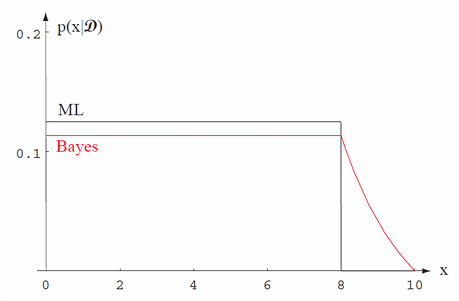
最后的分布:
p
(
x
∣
D
)
=
∫
θ
p
(
x
∣
θ
)
p
(
θ
∣
D
)
d
θ
p
(
x
∣
D
)
=
{
0.1134
,
0
≤
x
≤
8
786.875
(
1
x
4
−
1
1
0
4
)
,
8
<
x
≤
10
0
,
otherwise
p(\mathbf{x}\vert D)=\int_{\theta}p(\mathbf{x}\vert \theta)p(\theta\vert D)d\theta\\ p(\mathbf{x}\vert D)=\begin{cases} 0.1134, & 0\leq \mathbf{x}\leq8\\ 786.875\left(\frac{1}{\mathbf{x}^{4}}-\frac{1}{10^{4}}\right), & 8 < \mathbf{x}\leq10\\ 0, & \text{otherwise} \end{cases}
p(x∣D)=∫θp(x∣θ)p(θ∣D)dθp(x∣D)=⎩
⎨
⎧0.1134,786.875(x41−1041),0,0≤x≤88<x≤10otherwise
最大似然估计做法
对于数据,其似然函数为:
l
(
θ
)
=
p
(
x
1
,
x
2
,
x
3
,
x
4
∣
θ
)
=
1
θ
4
l(\theta)=p(x_{1},x_{2},x_{3},x_{4}\vert \theta)=\frac{1}{\theta^{4}}
l(θ)=p(x1,x2,x3,x4∣θ)=θ41
显然,
l
(
θ
)
l(\theta)
l(θ)单调递减,
θ
\theta
θ越小,
l
(
θ
)
l(\theta)
l(θ)越大。但同时,
θ
\theta
θ一定要大于等于最大观测数据。在现有样本
{
4
,
7
,
2
,
8
}
\{4,7,2,8\}
{4,7,2,8}中,使似然函数
l
(
θ
)
l(\theta)
l(θ)取值最大的
θ
\theta
θ只能等于8。所以由于是均匀分布,所以
θ
\theta
θ的最大似然估计值为8。
图中展示了最大似然估计(ML)和贝叶斯估计(Bayes)在样本后验分布上的区别。文中提到最大似然方法估计的是 θ \theta θ空间中的一个点,而贝叶斯方法估计的是一个分布。