MATLAB代码实现三次样条插值

参照《数值分析第五版（李庆扬）》P42 2.6.2样条插值函数的建立
目的是可以通过读取文本文件中提前存储的坐标点，来实现三边界种类型的三次样条插值

F.m

function result = F(newton, a, b)%1阶差商求值
    result = (newton(b, 2) - newton(a, 2)) / (newton(b, 1) - newton(a, 1));
end

S.m

function s = S(h, M1, M2, x1, x2, y1, y2, x)%M1, M2 = Mj, Mj+1; X1, X2 = Xj, Xj+1; H = Hj: Y1, Y2 = Yj, Yj+1; 
    s = M1 * (x2 - x).^3 ./ (6 * h) + M2 * (x - x1).^3 ./ (6 * h) + (y1 - M1 * h^2 / 6) .* (x2 - x) ./ h...
        + (y2 - M2 * h^2 / 6) .* (x - x1) ./h;
    s = s .* (heaviside(x - x1) - heaviside(x - x2));
end

spline.m这个是主函数

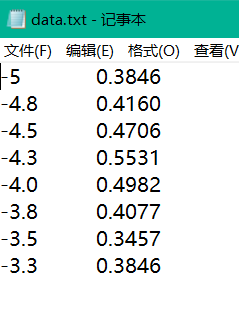
% 读取文本文件中存储的横纵坐标，txt的格式为：
% x1    y1
% x2    y2
% ... 
% xn    yn
% xn+1  yn+1
%横纵坐标用Tab隔开
FileData = load('data.txt');
X = FileData(:,1);
Y = FileData(:,2);
NewTon = [X, Y];
PointNumber = length(X); %n + 1 个点
n = PointNumber-1;
X_min = min(X);
X_max = max(X);
Y_min = min(Y);
Y_max = max(Y);
kind = input("请输入边界条件类型:1(已知两端的一阶导数值),2（已知两端二阶导数值）或3（f(x)是以Xn-X0为周期的周期函数)）\n");
if(kind ==3 && abs(Y(1) - Y(n+1)) >= 1e-5)
    disp("两端函数值不一致，错误！");
    return;
end
h = [0];
u = [0];
Lamda = [0];
d = [0];

%求hi
for i = 0:n - 1
    h(i+1) = X(i+2) - X(i+1);%h参数加了1 
end
%求ui 和 Lamdai
for j = 1:n - 1
    u(j) = h(j) / (h(j) + h(j+1));%h参数加了1 
    Lamda(j) = h(j+1) / (h(j) + h(j+1));%h参数加了1 
end
%求di
for j = 1:n - 1
    d(j) = 6 * (F(NewTon, j+1, j+2) - F(NewTon, j, j+1)) / (h(j) + h(j+1));%h参数加了1
end

%%%%%%%%%% 第一、二种情况
if(kind == 1 || kind == 2)
    if(kind == 1)
        f0D1 = input("请输入f(x0)一阶导数值\n");%3;%f(x0)一阶导数
        fnD1 = input("请输入f(xn)一阶导数值\n");%-4;%f(xn)一阶导数
        Lamda0 = 1;
        d0 = (6 / h(0+1)) * (F(NewTon, 0+1, 1+1) - f0D1);
        un = 1;
        dn = (6 / h(n-1+1)) * (fnD1 - F(NewTon, n-1+1, n+1));
    else%第二种情况
        f0D2 = input("请输入f(x0)二阶导数值\n");%3;%f(x0)一阶导数
        fnD2 = input("请输入f(xn)二阶导数值\n");%-4;%f(xn)一阶导数
        Lamda0 = 0;
        d0 = 2 * f0D2;
        un = 0;
        dn = 2 * fnD2;
    end
    %生成系数矩阵A
    A = 2 .* eye(n+1, n+1);%生成元素是2的对角阵
    for j = 2 : n
        A(j, j+1) = Lamda(j-1);
    end
    for j = 1:n - 1
        A(j+1, j) = u(j);
    end
    A(1, 2) = Lamda0;
    A(n+1, n) = un;
    %生成常数列向量b
    b = [d0, d, dn]';
    %求解矩阵方程
    M=A \ b;
    x = X_min - 10 : 0.001 : X_max + 10;
    %画出坐标点
    plot(X,Y,'x');
    hold on;
    Sx = 0;
    %构建插值多项式
    for j = 1:n
        Sx = Sx + S(h(j), M(j), M(j+1), X(j), X(j+1), Y(j), Y(j+1), x);%function s = S(h, M1, M2, x1, x2, y1, y2, x);
    end
    plot(x,Sx);
    title(['三次样条插值 边界条件类型：',num2str(kind)]);
    axis([X_min-0.1*(X_max-X_min) X_max+0.1*(X_max-X_min) Y_min-0.1*(X_max-X_min) Y_max+0.1*(X_max-X_min)]);
    grid on;
    legend("坐标点","插值函数");
end
%%%%%%%%%% 第三种情况
if(kind == 3)
    Lamdan = h(1) / (h(n) + h(1));
    un = 1 - Lamdan;
    dn = 6 * (F(NewTon, 1, 2) - F(NewTon, n, n+1)) / (h(1) + h(n));
    %生成系数矩阵A
    A = 2 .* eye(n, n);%生成元素是2的对角阵
    for j = 1:n-1
        A(j, j+1) = Lamda(j);
    end
    for j = 1:n-2
        A(j+1, j) = u(j+1);
    end
    A(1, n) = u(1);
    A(n, 1) = Lamdan;
    A(n, n-1) = un;
     %生成常数列向量b
    b = [d, dn]';
     %求解矩阵方程
    M = A \ b;
    M = [M(1), M']';
    x = X_min - 10 : 0.001 : X_max + 10;
    %画出坐标点
    plot(X,Y,'x');
    hold on;
    Sx = 0;
    %构建插值多项式
    for j = 1:n
        Sx = Sx + S(h(j), M(j), M(j+1), X(j), X(j+1), Y(j), Y(j+1), x);%function s = S(h, M1, M2, x1, x2, y1, y2, x);
    end
    plot(x,Sx);
    title(['三次样条插值 边界条件类型：',num2str(kind)]);
    axis([X_min-0.1*(X_max-X_min) X_max+0.1*(X_max-X_min) Y_min-0.1*(X_max-X_min) Y_max+0.1*(X_max-X_min)]);
    grid on;
    legend("坐标点","插值函数");
end

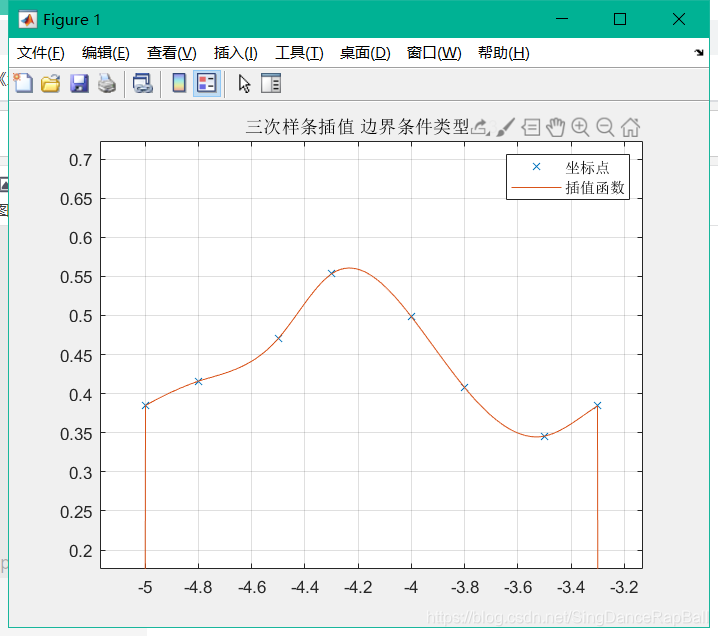
第三种边界类型测试：
在这里插入图片描述
运行结果：

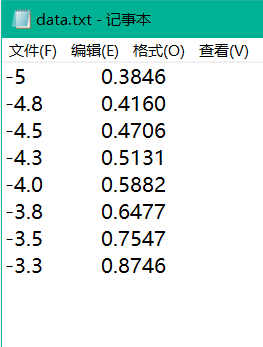
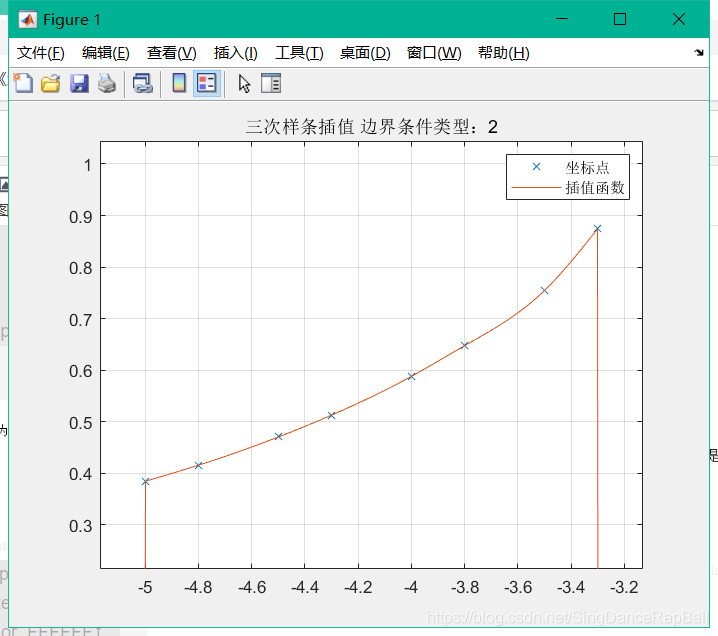
第二种边界类型测试：

MATLAB代码实现三次样条插值

悦读