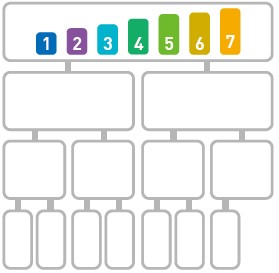
归并排序

稳定排序，时间复杂度O(nlogn)
归并排序算法会把序列分成长度相同的两个子序列（如果序列长度为奇数，则一个序列比另一个序列多一个元素），当无法继续往下分时（也就是每个子序列中只有一个数据时），就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行，直到所有子序列都归并为一个整体为止。
步骤：

将原序列分成两个子序列
将每一个子序列看成一个整体，继续拆分
直至每个子序列，只有一个数据时，如下面所示。
下面开始对分割的元素开始合并，合并时需要将数字按从大到小排列，把6和4合并，合并后的顺序是[4，6]
把3和7合并，合并后的顺序是[3,7]
合并这种含有多个数字的子序列时，要先比较首位数字，再移动较小的数字。
由于4>3，所有将3先合并到序列中
然后再次比较序列中剩下的首位数字
由于7>4，所以将4合并到序列中
然后比较6和7，因为7>6，所以先将6合并到序列中，然后再将7合并到序列中
递归执行上面的操作，直到所有的数字都合为一个整体为止，最后的结果如下：

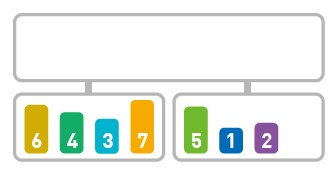
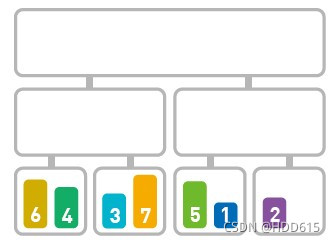
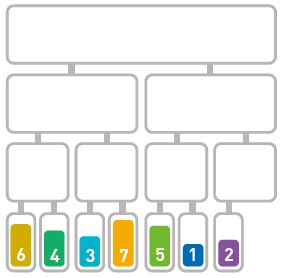
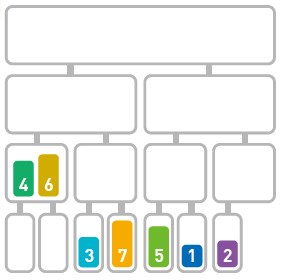
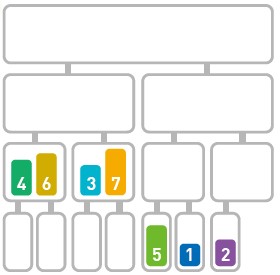
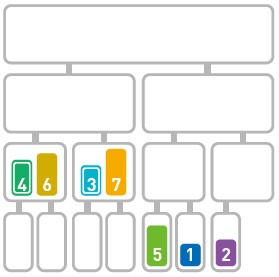
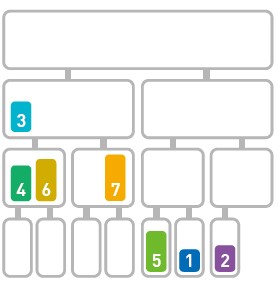
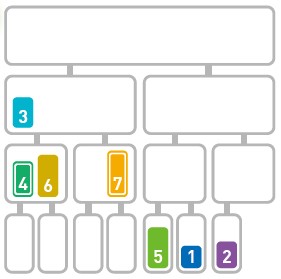
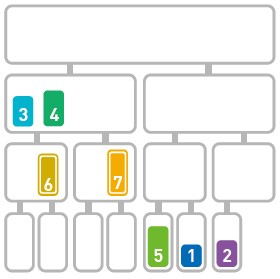
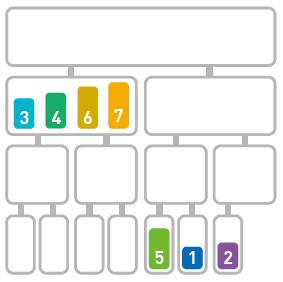
代码

def merge(arr,l,m,r):
	# 归并序列
	# l -- 序列的最左 下标
	# m -- 序列的中间 下标
	# r -- 序列的最右 下标
	left_arr = []
	right_arr = []
	for i in range(l,m+1):
		left_arr.append(arr[i])
	for j in range(m+1,r+1):
		right_arr.append(arr[j])
	
	i,j,k = 0,0,l
	n1 = len(left_arr)
	n2 = len(right_arr)
	while i < n1 and j < n2:
		if left_arr[i] < right_arr[j]:
			arr[k] = left_arr[i]
			i += 1
		else:
			arr[k] = right_arr[j]
			j += 1
		k += 1
	while i < n1:
		arr[k] = left_arr[i]
		i += 1
		k += 1
	while j < n2:
		arr[k] = right_arr[j]
		j += 1
		k += 1

def merge_sort(arr,l,r):
	if l < r:
		m = int((l+r)/2)
		merge_sort(arr,l,m)
		merge_sort(arr,m+1,r)
		merge(arr,l,m,r)

if __name__ == "__main__":
	arr = [15,8,32,42,25,41]
	merge_sort(arr,0,len(arr)-1)
	print("排序之后：",arr)