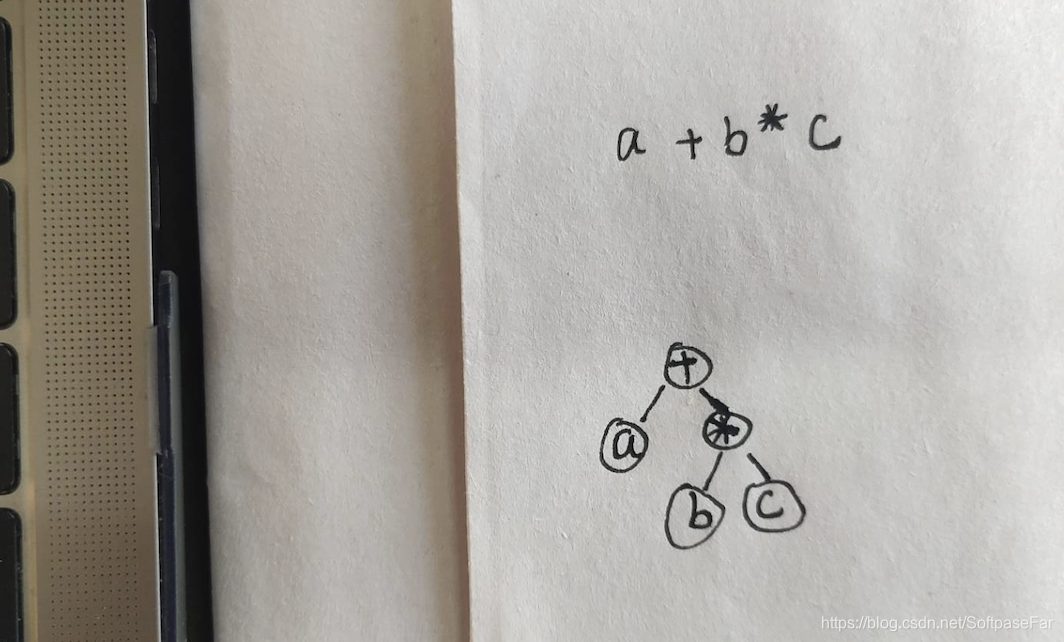问题描述

输入规则的算术表达式，生成算术表达式对应的二叉树。

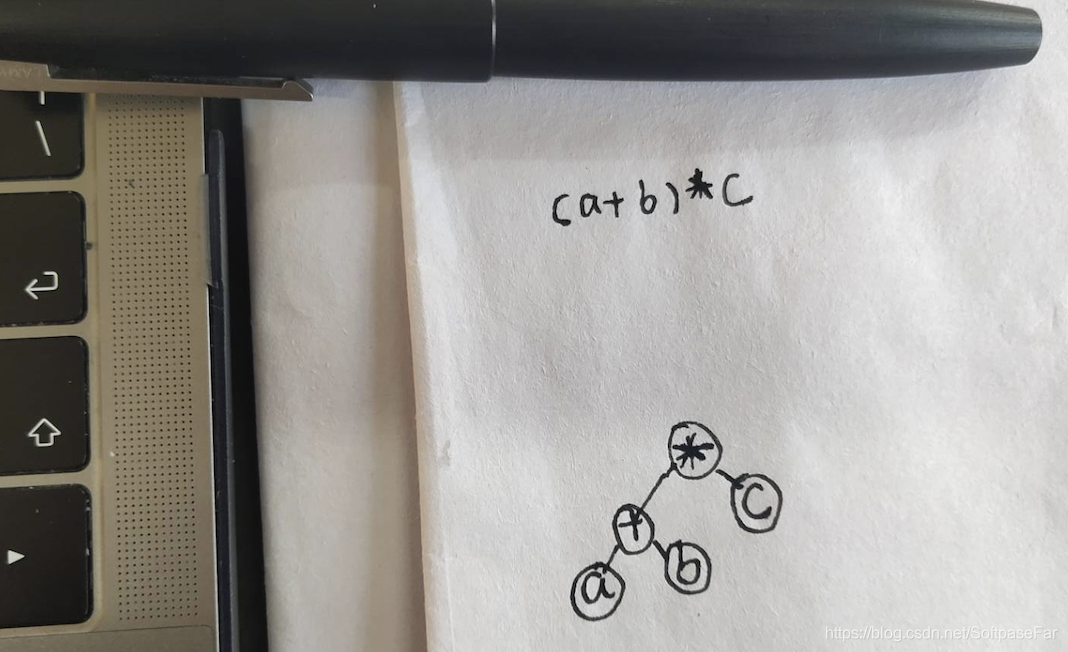
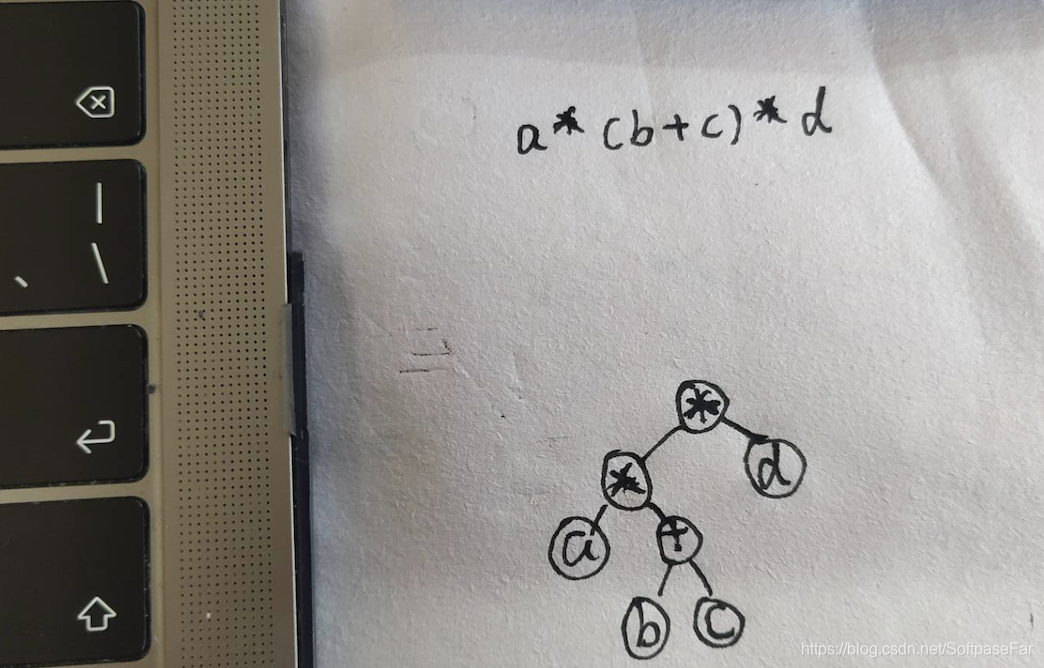
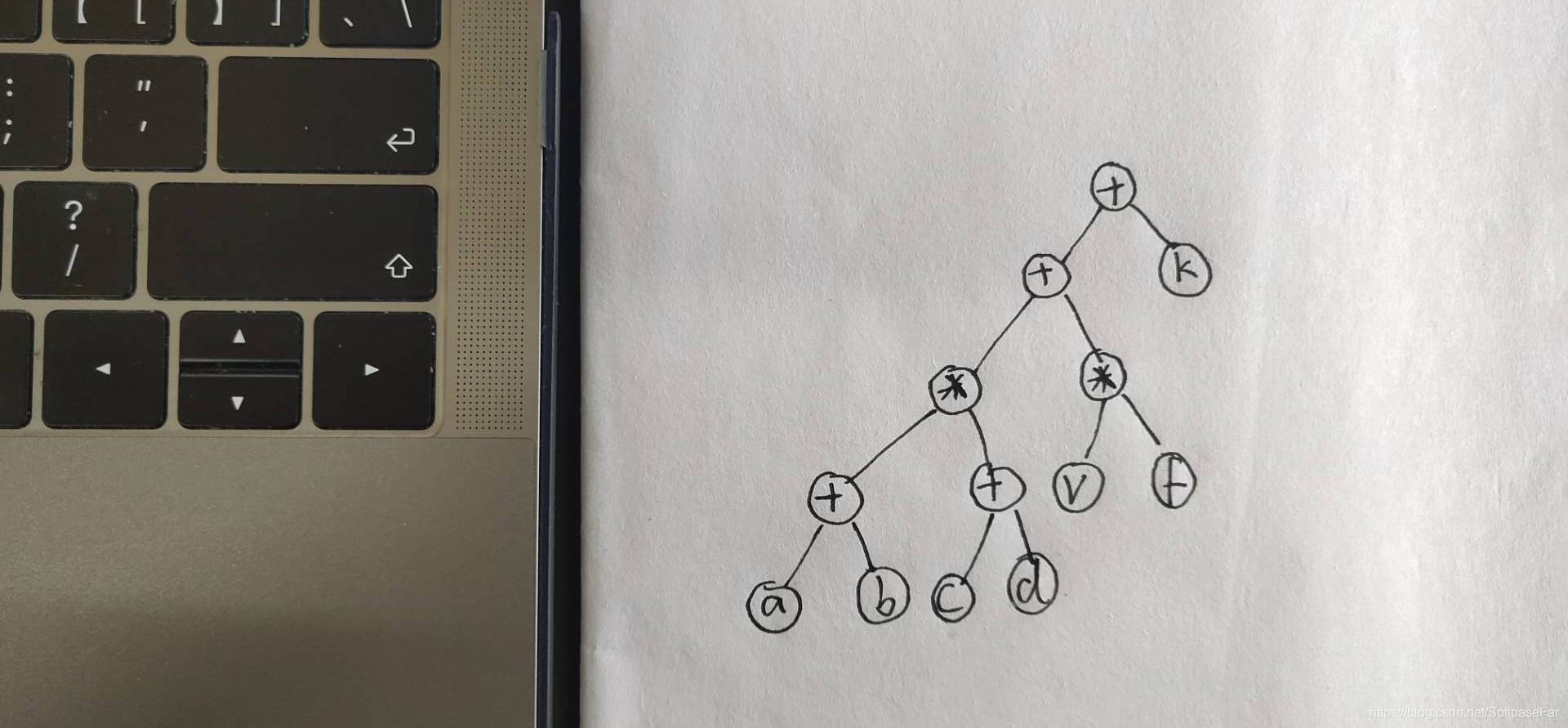
可以先给大家看几个例子：

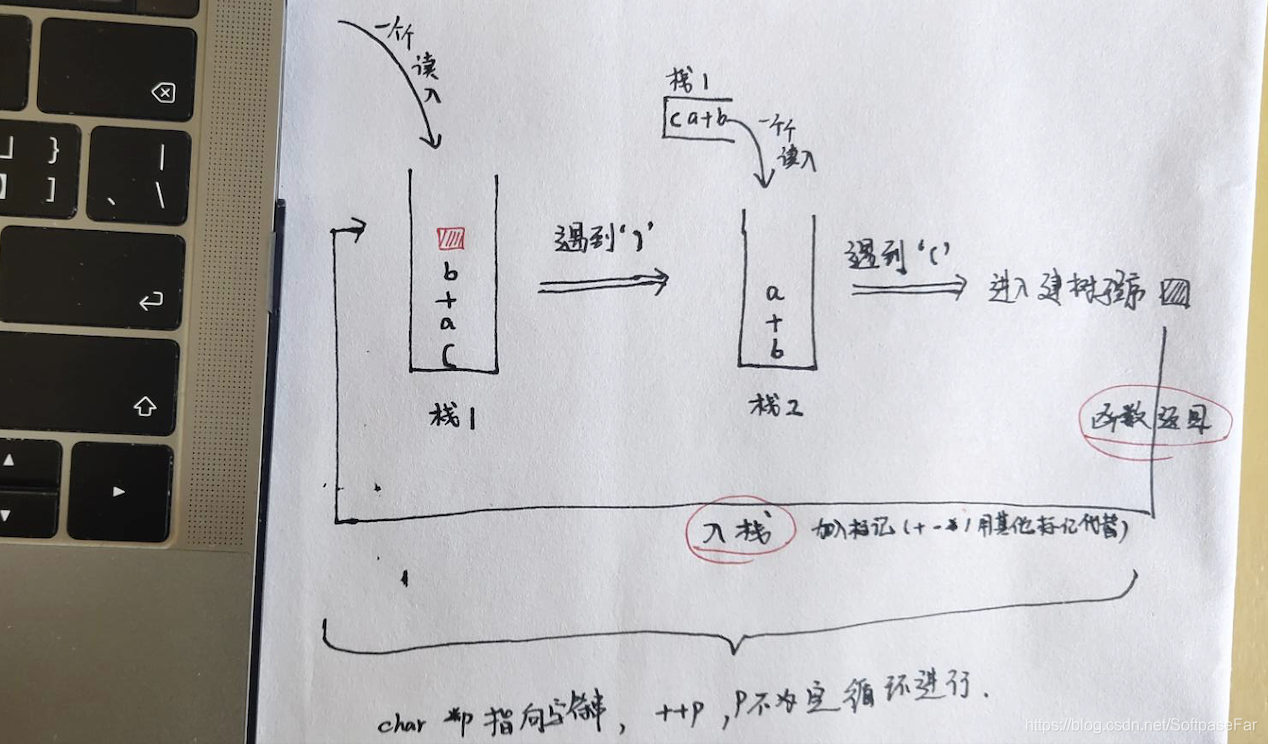
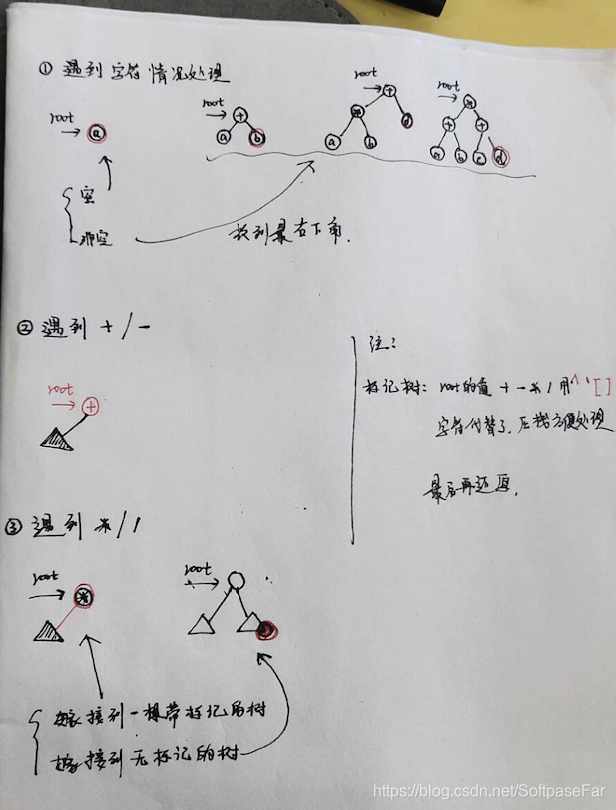
算法思想

图示算法思想

整体形态图解

建树函数图解

代码实现

我们的待处理表达式：(a+b) * (c+d)+v * f+k
注意：表达式之间不能有空白。

小贴士：直接看代码有些费劲，可以只看算法思想，自己实现，遇到障碍再看对应的代码。如果有什么好的方法大家可以下边留言。万分感谢(#^ * ^#)。

#include <iostream>
#include <string>

using namespace std;
#define MaxSize 30

//树节点信息
struct TreeNode {
    char val;
    TreeNode *left;
    TreeNode *right;

    TreeNode(char x = '\0') : val(x), left(NULL), right(NULL) {}
};


//定义栈
struct SqStack {
    TreeNode data[MaxSize];
    int top;
};

SqStack S_D, S_A;

//栈相关操作
//初始化
void InitStack(SqStack &s) {
    s.top = -1;
}

//栈判空
bool StackEmpty(SqStack s) {
    if (s.top == -1) {
        return true;
    } else {
        return false;
    }
}

//进栈
bool Push(SqStack &s, TreeNode x) {
    if (s.top == MaxSize - 1) {
        return false;
    }
    s.data[++s.top] = x;
    return true;
}

//出栈
bool Pop(SqStack &s, TreeNode &x) {
    if (s.top == -1) {
        return false;
    }
    x = s.data[s.top--];
    return true;
}

//定义队列
struct SqQueue {
    TreeNode data[MaxSize];
    int front, rear;

};
SqQueue Q;


//队列相关操作
//初始化
void InitQueue(SqQueue &Q) {
    Q.rear = Q.front = 0;
}

//判队空
bool isEmpty(SqQueue Q) {
    if (Q.front == Q.rear) return true;
    else return false;
}

//入队
bool EnQueue(SqQueue &Q, TreeNode x) {
    if ((Q.rear + 1) % MaxSize == Q.front) return false;
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

//出队
bool DeQueue(SqQueue &Q, TreeNode &x) {
    if (Q.rear == Q.front) return false;
    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}


//访问节点
void Visit(TreeNode *T) {
    cout << T->val << " ";
}

//先序遍历
void PreOrder(TreeNode *T) {
    if (T != NULL) {
        Visit(T);
        PreOrder(T->left);
        PreOrder(T->right);
    }
}

//中序遍历
void InOrder(TreeNode *T) {
    if (T != NULL) {
        InOrder(T->left);
        Visit(T);
        InOrder(T->right);
    }
}

//后序遍历
void PostOrder(TreeNode *T) {
    if (T != NULL) {
        PostOrder(T->left);
        PostOrder(T->right);
        Visit(T);
    }
}


//层序遍历
void LevelOrder(TreeNode *T) {
    InitQueue(Q);
    TreeNode p;
    EnQueue(Q, *T);
    while (!isEmpty(Q)) {
        DeQueue(Q, p);
        Visit(&p);
        if (p.left != NULL)
            EnQueue(Q, *p.left);
        if (p.right != NULL)
            EnQueue(Q, *p.right);
    }

}

//转换为替身
void RevToAn(TreeNode *r) {
    switch (r->val) {
        case '+':
            r->val = '^';
            break;
        case '-':
            r->val = '`';
            break;
        case '*':
            r->val = '[';
            break;
        case '/':
            r->val = ']';
            break;
    }
}


//还原本身
void ReToMy(TreeNode *T) {
    if (T != NULL) {
        switch (T->val) {
            case '^':
                T->val = '+';
                break;
            case '`':
                T->val = '-';
                break;
            case '[':
                T->val = '*';
                break;
            case ']':
                T->val = '/';
                break;
        }
        ReToMy(T->left);
        ReToMy(T->right);
    }

}


//构建二叉树
TreeNode *DealWith(SqStack &s) {
    TreeNode *root = NULL;
    while (!StackEmpty(s)) {
        TreeNode x;
        Pop(s, x);
        if (x.val == '+' || x.val == '-') {
            TreeNode *xplus = new TreeNode(x);
            xplus->val = x.val;
            xplus->left = root;
            root = xplus;
            continue;
        }

        if (x.val == '*' || x.val == '/') {  
            TreeNode *xby = new TreeNode(x);
            xby->val = x.val;
            if (root->val == '[' || root->val == ']' || root->val == '^' || root->val == '`') {
                xby->left = root;
                root = xby;
            } else {
                if (root->right) {
                    TreeNode *temp = root;
                    while (temp->right->right) {
                        temp = temp->right;
                    }
                    xby->left = temp->right;
                    temp->right = xby;
                } else {
                    root->right = xby;
                }
            }
            continue;
        }

        if (x.val >= ']' && x.val <= 'z') {
            TreeNode *xstr = new TreeNode(x);
            xstr->val = x.val;
            if (root == NULL) {
                root = xstr;
            } else {
                TreeNode *temp = root;
                while (temp->right) {
                    temp = temp->right;
                }
                temp->right = xstr;
            }
            continue;
        }
    }

    //替换一下root的北荣防止混淆
    RevToAn(root);
    return root;
}


//()区分优先级
void Divided(char *p, TreeNode *&root) {


    while ((*p) != '\0' || !StackEmpty(S_D)) {
        while ((*p) != '\0') {
            if ((*p) == ')') {
                ++p;
                break;
            } else {
                TreeNode x;
                x.val = *p;
                Push(S_D, x);
                ++p;
            }
        }

        while (!StackEmpty(S_D)) {
            TreeNode x;
            Pop(S_D, x);
            if (x.val == '(') {
                TreeNode temp = *DealWith(S_A);
                Push(S_D, temp);

                break;
            }
            Push(S_A, x);
        }
    }

    if (!StackEmpty(S_A)) {
        root = DealWith(S_A);
    }

}

void PrintInfo(TreeNode *root) {

    //还原本身
    ReToMy(root);

    cout << endl;
    cout << "先序遍历：";
    PreOrder(root);
    cout << endl;
    cout << "中序遍历：";
    InOrder(root);
    cout << endl;
    cout << "后序遍历：";
    PostOrder(root);
    cout << endl;
    cout << "层序遍历：";
    LevelOrder(root);
    cout << endl;
}


int main() {
    //数据获取
    char str[] = "(a+b)*(c+d)+v*f+k";


    //初始化区分栈(S_D)和算法栈(S_A)
    InitStack(S_D);
    InitStack(S_A);

    //构建算术二叉树

    TreeNode *root = NULL;
    Divided(str, root);

    //先序，中序输出查看二叉树的正确性
    PrintInfo(root);

    return 0;
}

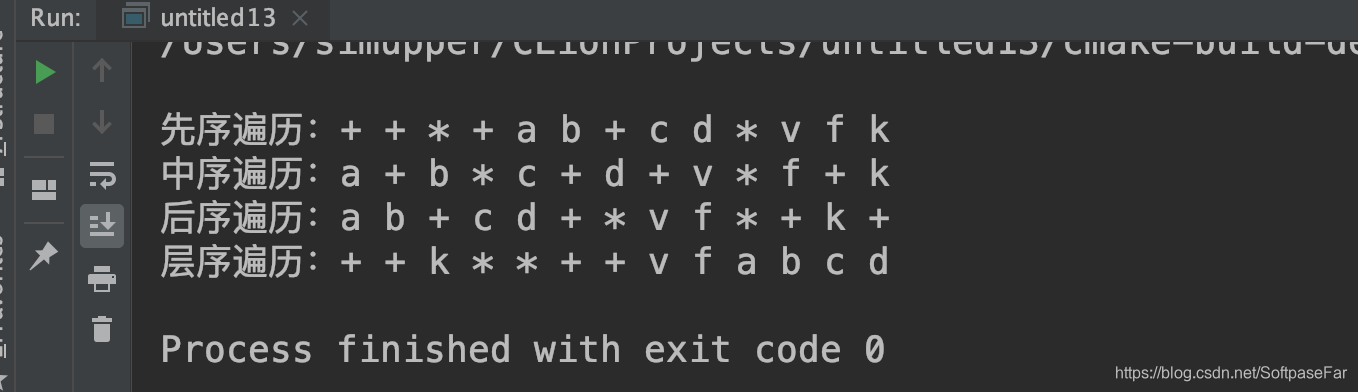
结果显示

预期结果

代码结果

大家可以把代码优化成输入自定义的表达式；
另外可以加层正则表达式的判断，这样代码在逻辑上，安全上都很完美了。(#^ .^#)

谢谢阅读(#^ .^#)