公式乱码严重,文章已转至
去噪扩散概率模型(Denoising Diffusion Probabilistic Model, DDPM)在2020年被提出,向世界展示了扩散模型的强大能力,带动了扩散模型的火热。笔者出于兴趣自学相关知识,结合网络上的参考资料和自己的理解介绍DDPM。需要说明的是,笔者能力很有限,学习过程中遇到了很多知识盲区,只能硬着头皮现学现卖。如果发现文中有错误,欢迎评论指出,大家一起学习,共同进步。
前置知识
① 贝叶斯公式
若满足马尔科夫链关系 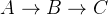
② 高斯分布的概率密度函数、高斯函数的叠加公式
给定均值为 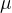
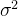
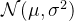
很多时候,为了方便起见,可以将前面的常数系数去掉,写成:
给定两个高斯分布 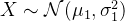
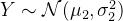
满足:
③ KL散度与交叉熵
详细讲解可参照我之前的博客。假设随机变量的真实概率分布为 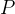
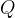
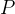
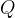
对于两个单一变量的高斯分布 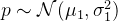
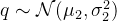
④ 参数重整化(重参数技巧)
若要从高斯分布 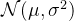
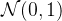
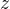

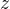
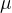
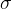
基本介绍
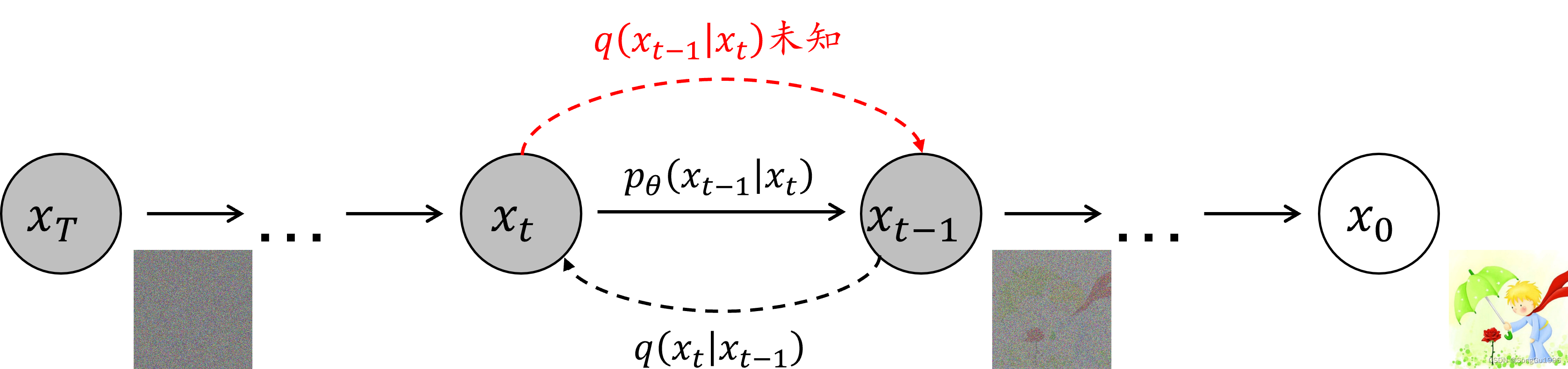
如下图所示,DDPM模型主要分为两个过程:加噪过程(从右往左)和去噪过程(从左往右)。
★ 加噪过程:给定真实图像 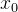
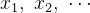
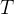
★ 去噪过程:针对噪声图像 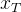
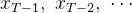
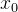
前向过程(扩散过程,加噪过程)
给定初始图像 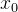
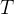
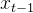
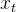
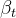
根据定义式,加噪过程可以看作在上一步的状态 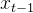

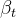
此外,加噪过程是一个马尔科夫链过程,所以联合概率分布可以写成下式:
定义 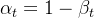
,代入
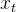
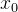
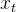
上式从第二项到最后一项都是独立的高斯噪声,它们的均值都为0,方差为各自系数的平方。根据高斯分布的叠加公式,它们的和满足均值为0,方差为各项方差之和的高斯分布。又有上式每一项系数的平方和(包括第一项)为1,证明如下,注意始终有 :
那么,将 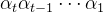
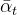
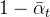
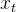
由该式可以看出,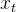
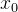
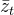
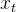
当加噪步数 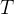
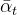
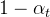
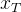
反向过程(逆扩散过程,去噪过程)
前向过程对原始图像 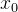
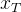
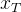
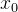
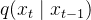
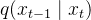
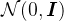
有文献证明,如果 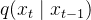
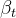
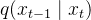
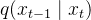
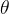
反向过程仍然是一个马尔科夫链过程,网络以当前时刻 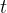
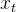
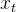
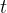
而真实的反向过程,或者称作扩散过程的后验条件概率,可以写成:
其中,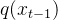
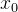
又根据前向过程的推导,有下面三个式子满足:
将三个式子代入,并结合前置知识中的高斯函数概率密度函数,展开后合并同类项,有下式:
此式符合前置知识中高斯函数概率密度函数的展开形式,有以下两个式子满足:
对第一个式子,有:
对第二个式子,有:
所以,在给定 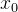
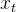
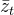
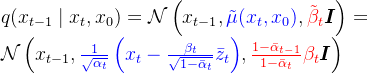
优化目标
我们的目标是得到尽可能真实的 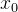
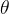
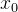
由 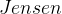
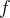
再对两边同时取负,得到负对数似然函数,满足:
式子右侧称为变分上界,最大化对数似然函数可以转换为最小化变分上界,结合马尔科夫链的贝叶斯公式将变分上界展开:
因为和的期望等于期望的和,可得:
因为期望目标与部分时间步的概率无关可以直接省去,可得:
中间的求和项根据前置知识中的贝叶斯公式改写,可得:
对 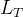
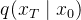
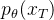
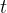
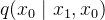
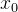
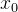
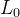
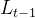
为了简化计算,DDPM对 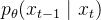
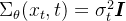

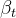
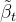

结合前置知识中高斯分布的KL散度公式,有:
将此式代回之前变分上界的式子,则优化目标 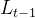
也就是说,我们希望网络参数化高斯分布的均值 
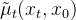
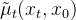
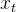
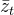
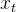
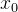
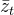
其中,参数化高斯分布的均值 
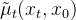
这里的 
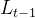
![= \mathbb{E}_{ x_{0}, \bar{z}_{t} \sim \mathcal{N}(0,\boldsymbol{I})} \left [ \frac{1}{2\sigma_{t} ^{2}}\left \| \frac{\beta _{t}}{\sqrt{\alpha _{t}} \sqrt{1-\bar{\alpha }_{t}}}\left (\bar{z}_{t} - z_{\theta}\left ( \color{magenta}{x_{t}(x_{0},\bar{z}_{t})}, t \right ) \right ) \right \| ^{2} \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lM0QlMjAlNUNtYXRoYmIlN0JFJTdEXyU3QiUyMHhfJTdCMCU3RCUyQyUyMCU1Q2JhciU3QnolN0RfJTdCdCU3RCUyMCU1Q3NpbSUyMCU1Q21hdGhjYWwlN0JOJTdEJTI4MCUyQyU1Q2JvbGRzeW1ib2wlN0JJJTdEJTI5JTdEJTIwJTVDbGVmdCUyMCU1QiUyMCU1Q2ZyYWMlN0IxJTdEJTdCMiU1Q3NpZ21hXyU3QnQlN0QlMjAlNUUlN0IyJTdEJTdEJTVDbGVmdCUyMCU1QyU3QyUyMCU1Q2ZyYWMlN0IlNUNiZXRhJTIwXyU3QnQlN0QlN0QlN0IlNUNzcXJ0JTdCJTVDYWxwaGElMjBfJTdCdCU3RCU3RCUyMCU1Q3NxcnQlN0IxLSU1Q2JhciU3QiU1Q2FscGhhJTIwJTdEXyU3QnQlN0QlN0QlN0QlNUNsZWZ0JTIwJTI4JTVDYmFyJTdCeiU3RF8lN0J0JTdEJTIwLSUyMHpfJTdCJTVDdGhldGElN0QlNUNsZWZ0JTIwJTI4JTIwJTVDY29sb3IlN0JtYWdlbnRhJTdEJTdCeF8lN0J0JTdEJTI4eF8lN0IwJTdEJTJDJTVDYmFyJTdCeiU3RF8lN0J0JTdEJTI5JTdEJTJDJTIwdCUyMCU1Q3JpZ2h0JTIwJTI5JTIwJTVDcmlnaHQlMjAlMjklMjAlNUNyaWdodCUyMCU1QyU3QyUyMCU1RSU3QjIlN0QlMjAlNUNyaWdodCUyMCU1RA%3D%3D)
可以将系数项去掉,进一步简化:
![L_{t-1}^{simple}= \mathbb{E}_{ x_{0}, \bar{z}_{t} \sim \mathcal{N}(0,\boldsymbol{I})} \left [ \left \| \bar{z}_{t} - z_{\theta}(\sqrt{\bar{\alpha }_{t}}x_{0} + \sqrt{1-\bar{\alpha }_{t}}\bar{z}_{t}, t) \right \| ^{2} \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9MXyU3QnQtMSU3RA%3D%3D%5E%7Bsimple%7D%3D%20%5Cmathbb%7BE%7D_%7B%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%20%5Csim%20%5Cmathcal%7BN%7D%280%2C%5Cboldsymbol%7BI%7D%29%7D%20%5Cleft%20%5B%20%5Cleft%20%5C%7C%20%5Cbar%7Bz%7D_%7Bt%7D%20-%20z_%7B%5Ctheta%7D%28%5Csqrt%7B%5Cbar%7B%5Calpha%20%7D_%7Bt%7D%7Dx_%7B0%7D%20+%20%5Csqrt%7B1-%5Cbar%7B%5Calpha%20%7D_%7Bt%7D%7D%5Cbar%7Bz%7D_%7Bt%7D%2C%20t%29%20%5Cright%20%5C%7C%20%5E%7B2%7D%20%5Cright%20%5D)
虽然背后的推导比较复杂,但是最终得到的优化目标非常简单,就是让网络预测的噪声与真实的噪声一致。
参考
大一统视角理解扩散模型Understanding Diffusion Models: A Unified Perspective 阅读笔记 - 知乎
什么是 Diffusion Models/扩散模型?_哔哩哔哩_bilibili
单变量高斯分布的KL散度_昕晛的博客-CSDN博客_高斯分布的kl散度
组会分享:生成扩散概率模型简介 Diffusion Models_哔哩哔哩_bilibili
简单基础入门理解Denoising Diffusion Probabilistic Model,DDPM扩散模型_xiongxyowo的博客-CSDN博客
轻松学习扩散模型(diffusion model),被巨怪踩过的脑袋也能懂——原理详解+pytorch代码详解(附全部代码) - 知乎
 https://zhuanlan.zhihu.com/p/636776166
https://zhuanlan.zhihu.com/p/636776166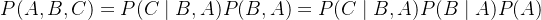
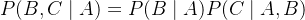
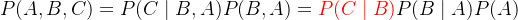
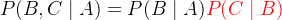
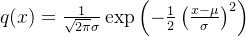
![\textcolor[rgb]{0, 0.39, 0}{D_{KL}(P,Q)} = \textcolor[rgb]{0.63, 0.12, 0.94}{-\sum P\log Q} - (-\sum P\log P) =\textcolor[rgb]{0.63, 0.12, 0.94}{\mathbb{E}_{P}[- \log Q]} - \mathbb{E}_{P}[- \log P]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN0ZXh0Y29sb3IlNUJyZ2IlNUQlN0IwJTJDJTIwMC4zOSUyQyUyMDAlN0QlN0JEXyU3QktMJTdEJTI4UCUyQ1ElMjklN0QlMjAlM0QlMjAlNUN0ZXh0Y29sb3IlNUJyZ2IlNUQlN0IwLjYzJTJDJTIwMC4xMiUyQyUyMDAuOTQlN0QlN0ItJTVDc3VtJTIwUCU1Q2xvZyUyMFElN0QlMjAtJTIwJTI4LSU1Q3N1bSUyMFAlNUNsb2clMjBQJTI5JTIwJTNEJTVDdGV4dGNvbG9yJTVCcmdiJTVEJTdCMC42MyUyQyUyMDAuMTIlMkMlMjAwLjk0JTdEJTdCJTVDbWF0aGJiJTdCRSU3RF8lN0JQJTdEJTVCLSUyMCU1Q2xvZyUyMFElNUQlN0QlMjAtJTIwJTVDbWF0aGJiJTdCRSU3RF8lN0JQJTdEJTVCLSUyMCU1Q2xvZyUyMFAlNUQ%3D)

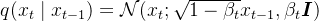
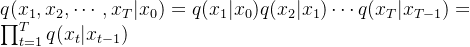



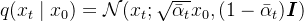
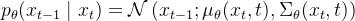
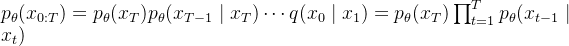

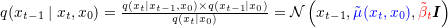
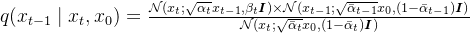
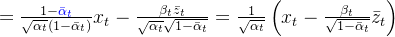
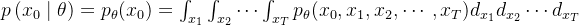
![= \int_{x_{1}}\int _{x_{2}}\cdots \int _{x_{T}}\textcolor[rgb]{0, 0.55, 0}{q(x_{1:T}\mid x_{0}) }\frac{p_{\theta}(x_{0}, x_{1}, x_{2},\cdots ,x_{T})}{\textcolor[rgb]{0, 0.55, 0}{q(x_{1:T}\mid x_{0})}} d_{x_{1}}d_{x_{2}}\cdots d_{x_{T}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lM0QlMjAlNUNpbnRfJTdCeF8lN0IxJTdEJTdEJTVDaW50JTIwXyU3QnhfJTdCMiU3RCU3RCU1Q2Nkb3RzJTIwJTVDaW50JTIwXyU3QnhfJTdCVCU3RCU3RCU1Q3RleHRjb2xvciU1QnJnYiU1RCU3QjAlMkMlMjAwLjU1JTJDJTIwMCU3RCU3QnElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTIwJTdEJTVDZnJhYyU3QnBfJTdCJTVDdGhldGElN0QlMjh4XyU3QjAlN0QlMkMlMjB4XyU3QjElN0QlMkMlMjB4XyU3QjIlN0QlMkMlNUNjZG90cyUyMCUyQ3hfJTdCVCU3RCUyOSU3RCU3QiU1Q3RleHRjb2xvciU1QnJnYiU1RCU3QjAlMkMlMjAwLjU1JTJDJTIwMCU3RCU3QnElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTdEJTIwZF8lN0J4XyU3QjElN0QlN0RkXyU3QnhfJTdCMiU3RCU3RCU1Q2Nkb3RzJTIwZF8lN0J4XyU3QlQlN0QlN0Q%3D)
![= \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [\frac{\textcolor[rgb]{0.55, 0, 0}{p_{\theta}(x_{0:T})}}{ q(x_{1:T}\mid x_{0})} \right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lM0QlMjAlNUNtYXRoYmIlN0JFJTdEXyU3QiUyMHElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTVDbGVmdCUyMCU1QiU1Q2ZyYWMlN0IlNUN0ZXh0Y29sb3IlNUJyZ2IlNUQlN0IwLjU1JTJDJTIwMCUyQyUyMDAlN0QlN0JwXyU3QiU1Q3RoZXRhJTdEJTI4eF8lN0IwJTNBVCU3RCUyOSU3RCU3RCU3QiUyMHElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTIwJTVDcmlnaHQlNUQ%3D)
![\log p_{\theta }(x_{0}) = \log \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [ \frac{ p_{\theta}(x_{0:T})}{ q(x_{1:T}\mid x_{0})} \right] \geq \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [\log \frac{ p_{\theta}(x_{0:T})}{ q(x_{1:T}\mid x_{0})}\right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsb2clMjBwXyU3QiU1Q3RoZXRhJTIwJTdEJTI4eF8lN0IwJTdEJTI5JTIwJTNEJTIwJTVDbG9nJTIwJTVDbWF0aGJiJTdCRSU3RF8lN0IlMjBxJTI4eF8lN0IxJTNBVCU3RCU1Q21pZCUyMHhfJTdCMCU3RCUyOSU3RCU1Q2xlZnQlMjAlNUIlMjAlNUNmcmFjJTdCJTIwcF8lN0IlNUN0aGV0YSU3RCUyOHhfJTdCMCUzQVQlN0QlMjklN0QlN0IlMjBxJTI4eF8lN0IxJTNBVCU3RCU1Q21pZCUyMHhfJTdCMCU3RCUyOSU3RCUyMCU1Q3JpZ2h0JTVEJTIwJTVDZ2VxJTIwJTVDbWF0aGJiJTdCRSU3RF8lN0IlMjBxJTI4eF8lN0IxJTNBVCU3RCU1Q21pZCUyMHhfJTdCMCU3RCUyOSU3RCU1Q2xlZnQlMjAlNUIlNUNsb2clMjAlNUNmcmFjJTdCJTIwcF8lN0IlNUN0aGV0YSU3RCUyOHhfJTdCMCUzQVQlN0QlMjklN0QlN0IlMjBxJTI4eF8lN0IxJTNBVCU3RCU1Q21pZCUyMHhfJTdCMCU3RCUyOSU3RCU1Q3JpZ2h0JTVE)
![- \log p_{\theta }(x_{0}) \leq \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [\log \frac{ q(x_{1:T}\mid x_{0})}{ p_{\theta}(x_{0:T})}\right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8tJTIwJTVDbG9nJTIwcF8lN0IlNUN0aGV0YSUyMCU3RCUyOHhfJTdCMCU3RCUyOSUyMCU1Q2xlcSUyMCU1Q21hdGhiYiU3QkUlN0RfJTdCJTIwcSUyOHhfJTdCMSUzQVQlN0QlNUNtaWQlMjB4XyU3QjAlN0QlMjklN0QlNUNsZWZ0JTIwJTVCJTVDbG9nJTIwJTVDZnJhYyU3QiUyMHElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTdCJTIwcF8lN0IlNUN0aGV0YSU3RCUyOHhfJTdCMCUzQVQlN0QlMjklN0QlNUNyaWdodCU1RA%3D%3D)
![L_{VLB} = \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [\log \frac{ \textcolor[rgb]{0, 0, 0.55}{q(x_{1:T}\mid x_{0})}}{ \textcolor[rgb]{0.55, 0, 0}{p_{\theta}(x_{0:T})}}\right] = \mathbb{E}_{ q(x_{1:T}\mid x_{0})}\left [\log \frac{ \textcolor[rgb]{0, 0, 0.55}{q(x_{1}\mid x_{0})q(x_{2}\mid x_{1})\cdots q(x_{T}\mid x_{T-1})}}{ \textcolor[rgb]{0.55, 0, 0}{p_{\theta}(x_{T})p_{\theta}(x_{T-1}\mid x_{T})\cdots p_{\theta}(x_{1}\mid x_{0})}}\right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9MXyU3QlZMQiU3RCUyMCUzRCUyMCU1Q21hdGhiYiU3QkUlN0RfJTdCJTIwcSUyOHhfJTdCMSUzQVQlN0QlNUNtaWQlMjB4XyU3QjAlN0QlMjklN0QlNUNsZWZ0JTIwJTVCJTVDbG9nJTIwJTVDZnJhYyU3QiUyMCU1Q3RleHRjb2xvciU1QnJnYiU1RCU3QjAlMkMlMjAwJTJDJTIwMC41NSU3RCU3QnElMjh4XyU3QjElM0FUJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTdEJTdCJTIwJTVDdGV4dGNvbG9yJTVCcmdiJTVEJTdCMC41NSUyQyUyMDAlMkMlMjAwJTdEJTdCcF8lN0IlNUN0aGV0YSU3RCUyOHhfJTdCMCUzQVQlN0QlMjklN0QlN0QlNUNyaWdodCU1RCUyMCUzRCUyMCU1Q21hdGhiYiU3QkUlN0RfJTdCJTIwcSUyOHhfJTdCMSUzQVQlN0QlNUNtaWQlMjB4XyU3QjAlN0QlMjklN0QlNUNsZWZ0JTIwJTVCJTVDbG9nJTIwJTVDZnJhYyU3QiUyMCU1Q3RleHRjb2xvciU1QnJnYiU1RCU3QjAlMkMlMjAwJTJDJTIwMC41NSU3RCU3QnElMjh4XyU3QjElN0QlNUNtaWQlMjB4XyU3QjAlN0QlMjlxJTI4eF8lN0IyJTdEJTVDbWlkJTIweF8lN0IxJTdEJTI5JTVDY2RvdHMlMjBxJTI4eF8lN0JUJTdEJTVDbWlkJTIweF8lN0JULTElN0QlMjklN0QlN0QlN0IlMjAlNUN0ZXh0Y29sb3IlNUJyZ2IlNUQlN0IwLjU1JTJDJTIwMCUyQyUyMDAlN0QlN0JwXyU3QiU1Q3RoZXRhJTdEJTI4eF8lN0JUJTdEJTI5cF8lN0IlNUN0aGV0YSU3RCUyOHhfJTdCVC0xJTdEJTVDbWlkJTIweF8lN0JUJTdEJTI5JTVDY2RvdHMlMjBwXyU3QiU1Q3RoZXRhJTdEJTI4eF8lN0IxJTdEJTVDbWlkJTIweF8lN0IwJTdEJTI5JTdEJTdEJTVDcmlnaHQlNUQ%3D)
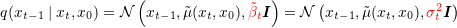
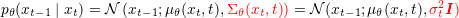
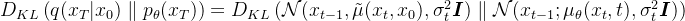
![L_{t-1} = \mathbb{E}_{ q(x_{t}\mid x_{0})}\left [ \frac{1}{2\sigma_{t} ^{2}}\left \| \tilde{\mu }_{t}(x_{t},x_{0}) - \mu _{\theta}(x_{t}, t) \right \| ^{2} \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9MXyU3QnQtMSU3RA%3D%3D%20%3D%20%5Cmathbb%7BE%7D_%7B%20q%28x_%7Bt%7D%5Cmid%20x_%7B0%7D%29%7D%5Cleft%20%5B%20%5Cfrac%7B1%7D%7B2%5Csigma_%7Bt%7D%20%5E%7B2%7D%7D%5Cleft%20%5C%7C%20%5Ctilde%7B%5Cmu%20%7D_%7Bt%7D%28x_%7Bt%7D%2Cx_%7B0%7D%29%20-%20%5Cmu%20_%7B%5Ctheta%7D%28x_%7Bt%7D%2C%20t%29%20%5Cright%20%5C%7C%20%5E%7B2%7D%20%5Cright%20%5D)
![L_{t-1} = \mathbb{E}_{ x_{0}, \bar{z}_{t} \sim \mathcal{N}(0,\boldsymbol{I})}\left [ \frac{1}{2\sigma_{t} ^{2}}\left \| \frac{1}{\sqrt{\alpha _{t}}}\left ( x_{t}\left ( x_{0}, \bar{z}_{t}\right ) - \frac{\beta _{t}}{\sqrt{1-\bar{\alpha }_{t}}}\bar{z}_{t} \right ) - \mu _{\theta}\left ( x_{t}\left ( x_{0}, \bar{z}_{t}\right ), t \right ) \right \| ^{2} \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9MXyU3QnQtMSU3RA%3D%3D%20%3D%20%5Cmathbb%7BE%7D_%7B%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%20%5Csim%20%5Cmathcal%7BN%7D%280%2C%5Cboldsymbol%7BI%7D%29%7D%5Cleft%20%5B%20%5Cfrac%7B1%7D%7B2%5Csigma_%7Bt%7D%20%5E%7B2%7D%7D%5Cleft%20%5C%7C%20%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Calpha%20_%7Bt%7D%7D%7D%5Cleft%20%28%20x_%7Bt%7D%5Cleft%20%28%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%5Cright%20%29%20-%20%5Cfrac%7B%5Cbeta%20_%7Bt%7D%7D%7B%5Csqrt%7B1-%5Cbar%7B%5Calpha%20%7D_%7Bt%7D%7D%7D%5Cbar%7Bz%7D_%7Bt%7D%20%5Cright%20%29%20-%20%5Cmu%20_%7B%5Ctheta%7D%5Cleft%20%28%20x_%7Bt%7D%5Cleft%20%28%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%5Cright%20%29%2C%20t%20%5Cright%20%29%20%5Cright%20%5C%7C%20%5E%7B2%7D%20%5Cright%20%5D)
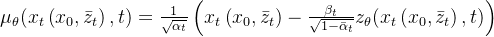
![L_{t-1} = \mathbb{E}_{ x_{0}, \bar{z}_{t} \sim \mathcal{N}(0,\boldsymbol{I})} \left [ \frac{1}{2\sigma_{t} ^{2}}\left \| \frac{1}{\sqrt{\alpha _{t}}}\left ( x_{t}\left ( x_{0}, \bar{z}_{t}\right ) - \frac{\beta _{t}}{\sqrt{1-\bar{\alpha }_{t}}}\bar{z}_{t} \right ) - \frac{1}{\sqrt{\alpha _{t}}}\left ( x_{t} - \frac{\beta _{t}}{\sqrt{1-\bar{\alpha }_{t}}}z_{\theta}(x_{t}\left ( x_{0}, \bar{z}_{t}\right ), t) \right ) \right \| ^{2} \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9MXyU3QnQtMSU3RA%3D%3D%20%3D%20%5Cmathbb%7BE%7D_%7B%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%20%5Csim%20%5Cmathcal%7BN%7D%280%2C%5Cboldsymbol%7BI%7D%29%7D%20%5Cleft%20%5B%20%5Cfrac%7B1%7D%7B2%5Csigma_%7Bt%7D%20%5E%7B2%7D%7D%5Cleft%20%5C%7C%20%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Calpha%20_%7Bt%7D%7D%7D%5Cleft%20%28%20x_%7Bt%7D%5Cleft%20%28%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%5Cright%20%29%20-%20%5Cfrac%7B%5Cbeta%20_%7Bt%7D%7D%7B%5Csqrt%7B1-%5Cbar%7B%5Calpha%20%7D_%7Bt%7D%7D%7D%5Cbar%7Bz%7D_%7Bt%7D%20%5Cright%20%29%20-%20%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Calpha%20_%7Bt%7D%7D%7D%5Cleft%20%28%20x_%7Bt%7D%20-%20%5Cfrac%7B%5Cbeta%20_%7Bt%7D%7D%7B%5Csqrt%7B1-%5Cbar%7B%5Calpha%20%7D_%7Bt%7D%7D%7Dz_%7B%5Ctheta%7D%28x_%7Bt%7D%5Cleft%20%28%20x_%7B0%7D%2C%20%5Cbar%7Bz%7D_%7Bt%7D%5Cright%20%29%2C%20t%29%20%5Cright%20%29%20%5Cright%20%5C%7C%20%5E%7B2%7D%20%5Cright%20%5D)