1. Introduction
由于固定的几何结构,传统的FCN受限于局部的感受野,只能提供短程的上下文信息。这对于提升分割任务的精度起到相反的影响。
为了弥补FCN的缺陷,ASPP和PPM模块被提出来,在网络的底层中加入有效的上下文特征。但是膨胀卷积并不能够产生密集的上下文信息。同时,基于池化的方法以非自适应的方式聚合上下文信息,并且认为所有图像像素具有相同的重要性,这不能满足不同像素需要不同的上下文依赖关系的要求。
为了包含密集的且逐像素的上下文信息,一些全连接的GNN方法被提出来,用估计的全图像上下文表示来增强传统的卷积特征。该方法中就包含了提出了自注意力机制的Non-local Networks工作,。
然而,这些基于GNN的Non-local神经网络需要产生庞大的注意力特征图来表示相互配对的像素间的关系,导致对于时间和空间复杂度都到 O ( N 2 ) O(N^2) O(N2), N N N代表输入特征的数量。
为了解决上述问题,我们的动机是使用几个连续的稀疏连接的图来代替单一的密集连接的图,使得可以减少计算资源。通过连续堆叠2个十字交叉的注意力模块,可以将时间和空间复杂度从 O ( N 2 ) O(N^2) O(N2)降低到 O ( N N ) O(N \sqrt N) O(NN)。我们共享交叉模块的参数以保持我们的模型苗条。
2. Approach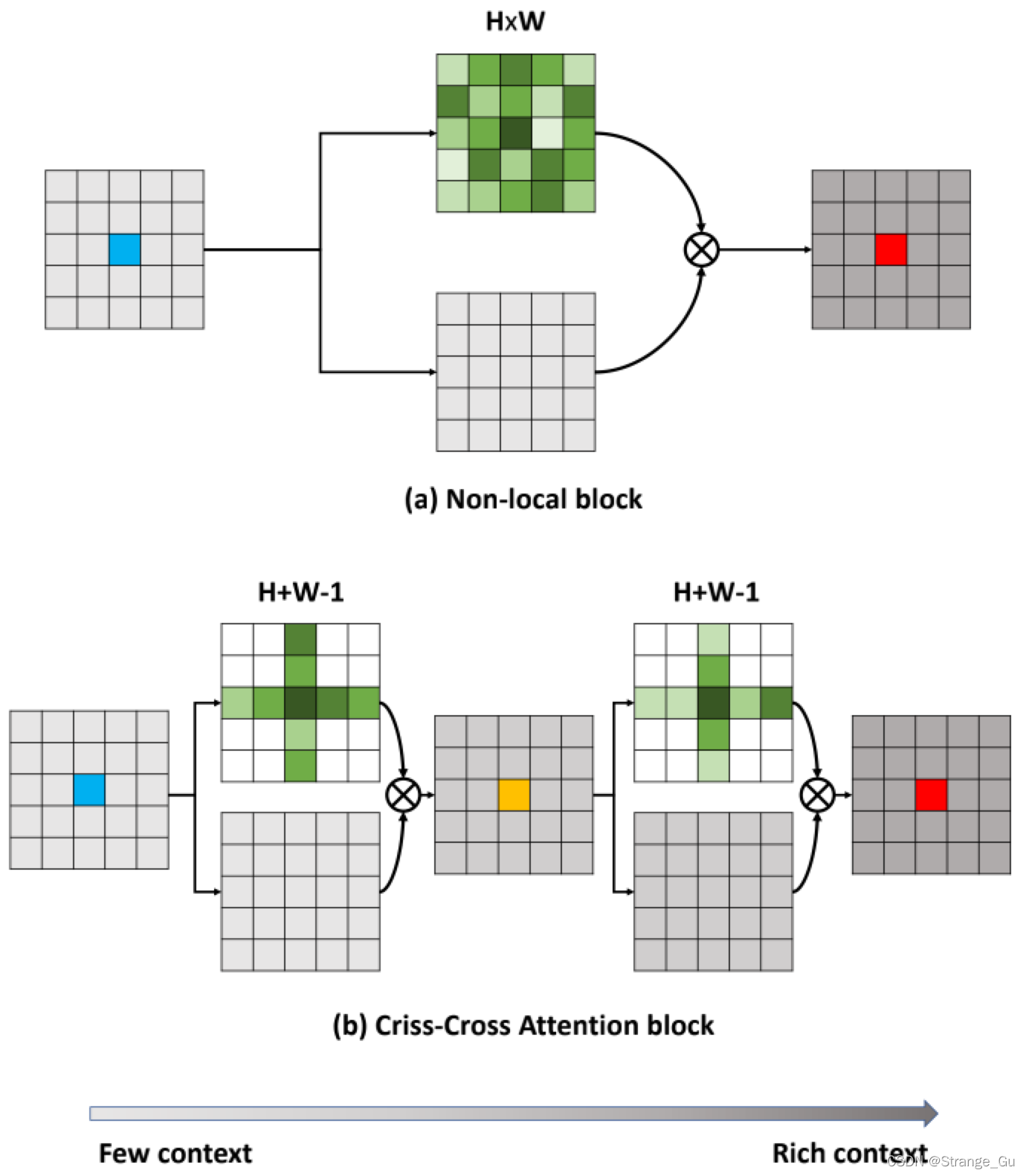
2.1 Network Architecture
接下来介绍在水平和垂直方向上捕获上下文信息的 2D 十字交叉注意力模块。 为了捕获密集的全局上下文信息,我们建议对十字交叉注意力模块采用循环操作。
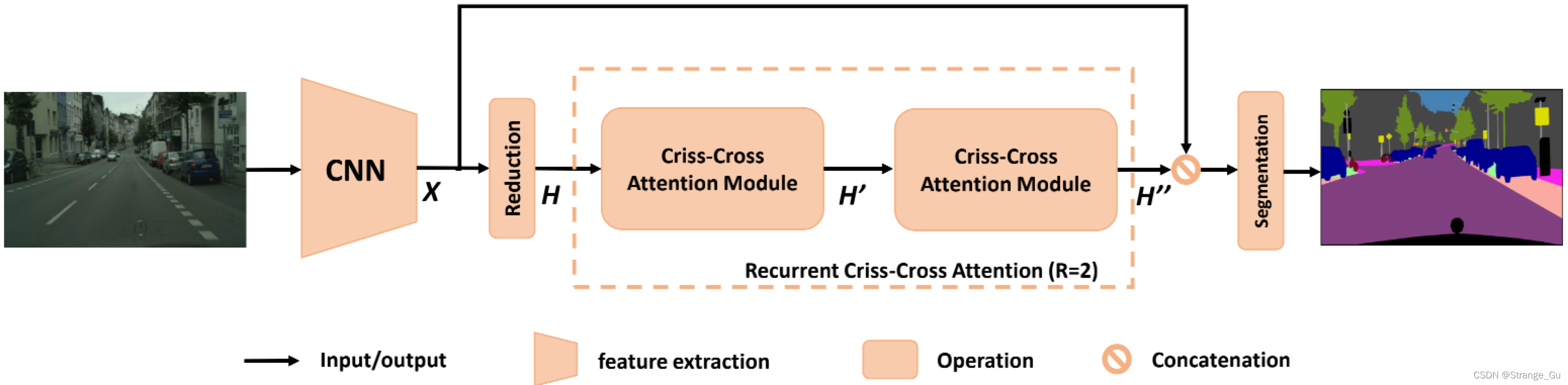
2.1.1. 输入图像经过一个DCNN网络来生成特征图空间维度是 H × W H \times W H×W的特征图 X X X。为了保留更多的细节信息并且能够生成密集的特征图,我们去除了最后两层的下采样操作并且加入了膨胀卷积在后面的卷积网络层中,最终特征图 X X X的大小为输入图像的 1 8 \frac{1}{8} 81。
2.1.2. 得到特征图 X X X后,使用 1 × 1 1 \times 1 1×1卷积降低通道数得到特征图 H H H。特征图 H H H再输入到十字交叉注意力模块后得到新的特征图 H ′ H^{'} H′,特征图 H ′ H^{'} H′中将上下文信息聚合到其十字交叉路径的每个像素中。
2.1.3. 特征图 H ′ H^{'} H′中每个像素中只包含了沿着它的水平方向和竖直方向上的上下文信息,对于要求精确度高的分割任务来说能力不够。为了得到更加丰富和密集的上下文信息,再将特征图 H ′ H^{'} H′又一次地输入到十字交叉注意力模块后,得到特征图 H ′ ′ H^{''} H′′。此时,特征图 H ′ ′ H^{''} H′′的每个像素都聚集了与所有位置像素的信息。
2.1.4. 两次十字交叉注意力模块共享参数,避免在模块中加入太多参数。并将其命名为 r e c u r r e n t c r i s s − c r o s s a t t e n t i o n ( R C C A ) recurrent \ criss-cross \ attention(RCCA) recurrent criss−cross attention(RCCA)模块。
2.1.5. 之后,我们将密集的上下文特征 H ′ ′ H^{''} H′′与特征图 X X X做 c o n c a t e n a t e concatenate concatenate操作后,后面架上卷积操作、 B N BN BN操作和激活函数来进行特征融合。
2.1.6. 最后,将融合后的特征图传入到分割层去预测最后的分割结果。
2.2 Criss-Cross Attention
\quad
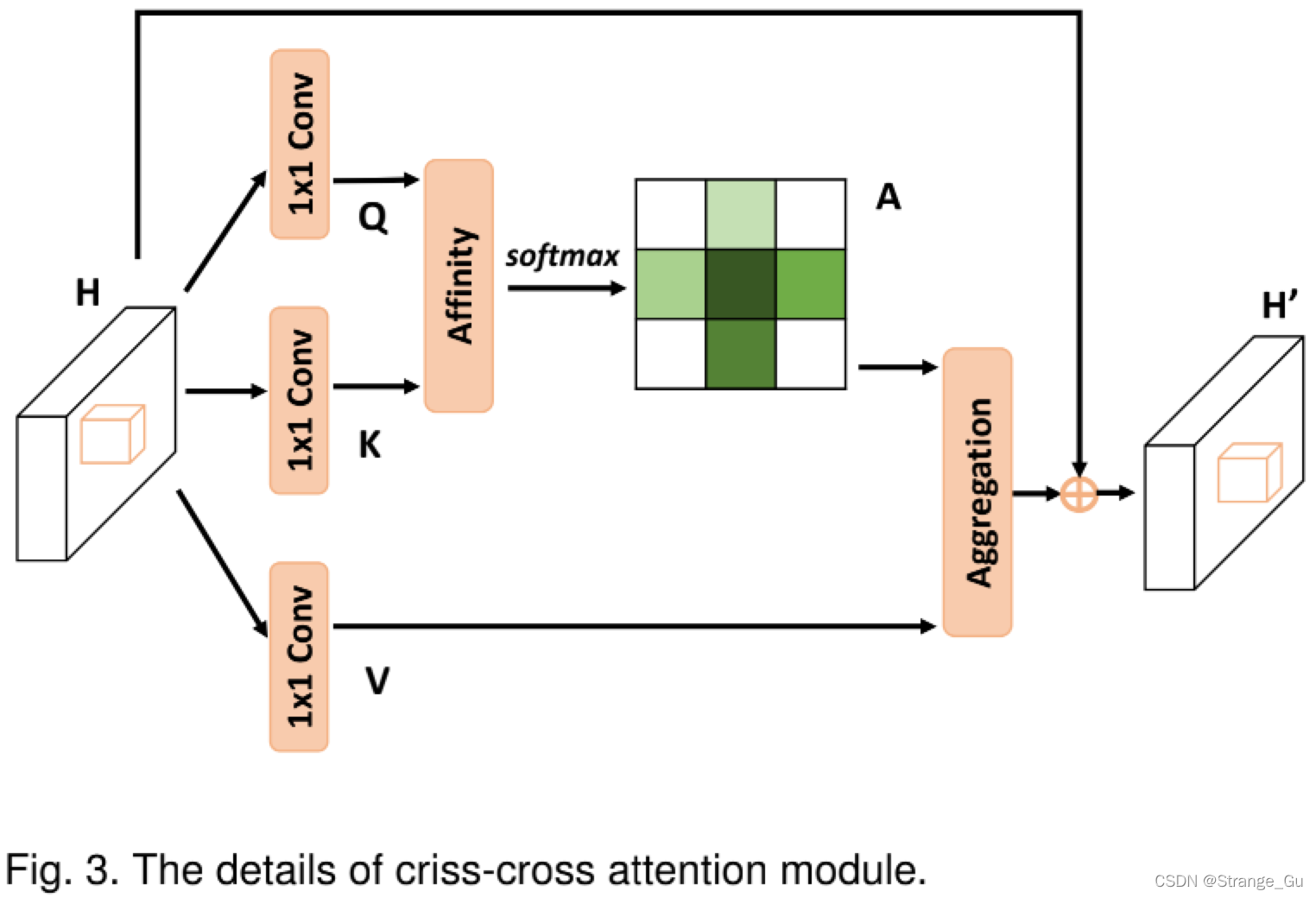
为了以轻量级的计算量和内存作为代价,就能够将全副图像的邻域特征间的依赖关系进行建模,我们提出了一个十字交叉注意力模块。十字交叉注意力模块在水平和竖直方向上收集上下文信息来增强逐像素的特征能力。如图3所示,大小为
R
C
×
W
×
H
R^{C\times W\times H}
RC×W×H特征图
H
H
H,经过两次
1
×
1
1 \times 1
1×1卷积各自生成特征图
Q
Q
Q和
K
K
K,
{
Q
,
K
}
∈
R
C
′
×
W
×
H
\{Q,K\}\in R^{C^{'} \times W \times H }
{Q,K}∈RC′×W×H,其中
C
′
C^{'}
C′小于
C
C
C。根据
Q
Q
Q和
K
K
K,生成注意力图
A
∈
R
(
H
+
W
−
1
)
×
(
W
×
H
)
A \in R^{(H+W-1)\times(W \times H)}
A∈R(H+W−1)×(W×H)。
步骤:
2.2.1 在 Q C ′ × W × H Q^{C^{'} \times W \times H} QC′×W×H的空间维度上每一个特征点 u u u的位置上,都可以得到一个向量 Q u ∈ R C ′ Q_u \in R^{C^{'}} Qu∈RC′。
2.2.2 同时,也在 K C ′ × W × H K^{C^{'}\times W \times H} KC′×W×H中在对应着特征点 u u u的所处位置从相同水平和竖直方向上收集特征,得到集合 Ω u ∈ R ( H + W − 1 ) × C ′ \Omega_u \in R^{(H+W-1) \times C^{'}} Ωu∈R(H+W−1)×C′。其中, Ω i , u ∈ R C ′ \Omega_{i,u} \in R^{C^{'}} Ωi,u∈RC′,是 Ω u \Omega_u Ωu的第 i i i个元素。
2.2.3 d i , u = Q u × Ω i , u T d_{i,u}=Q_u \times \Omega_{i,u}^{T} di,u=Qu×Ωi,uT。 d i , u ∈ D ( H + W − 1 ) × ( W × H ) d_{i,u} \in D^{(H+W-1)\times(W \times H)} di,u∈D(H+W−1)×(W×H)是 Q u Q_{u} Qu和 Ω i , u \Omega_{i,u} Ωi,u之间的相关程度。其中, i = [ 1 , … , H + W − 1 ] i=[1,…,H+W-1] i=[1,…,H+W−1]。之后再在通道维度上做一个softmax操作后,得到注意力特征图 A A A。
2.2.4 在特征图 H H H用 1 × 1 1 \times 1 1×1卷积,得到特征图 V V V, V ∈ R C × W × H V \in R^{C \times W \times H} V∈RC×W×H。在 V V V的空间维度上每一个特征点 u u u的位置上,都可以得到一个向量 V u ∈ R C V_u \in R^{C} Vu∈RC。并且还能从 u u u所处位置从相同水平和竖直方向上收集特征,得到集合 Φ u ∈ R ( H + W − 1 ) × C \Phi_u \in R^{(H+W-1)\times C} Φu∈R(H+W−1)×C。
2.2.5 将注意力特征图 A A A作用于特征图 V V V上,过程如公式 H u ′ = ∑ i = 0 H + W − 1 A i , u ϕ i , u + H u H_u^{'}=\sum_{i=0}^{H+W-1}A_{i,u} \phi_{i,u}+H_u Hu′=∑i=0H+W−1Ai,uϕi,u+Hu所示。至此,特征图 H u ′ H_u^{'} Hu′获得更大的上下文感受野,并且可以通过注意力特征图,从而有选择性地聚集上下文特征。
2.3 Recurrent Criss-Cross Attention(RCCA)
尽管通过十字交叉注意力模块作用后,能够在水平和竖直方向上捕获上下文特征,但并为考虑到其周围像素。为了处理这个问题,我们基于十字交叉注意力模块的基础上,既创新又简单地引入了RCCA操作。RCCA操作就是连续两个十字交叉注意力模块相连。首先,将特征图
H
H
H经过第一个十字交叉注意力模块后,输出特征图
H
′
H^{'}
H′,
H
′
H^{'}
H′与
H
H
H的形状相同。再将特征图H^'经过第二个十字交叉注意力模块,输出特征图
H
′
′
H^{''}
H′′。
H
′
′
H^{''}
H′′能够从所有像素中获取全图像上下文信息,以生成具有密集和丰富上下文信息的新特征。
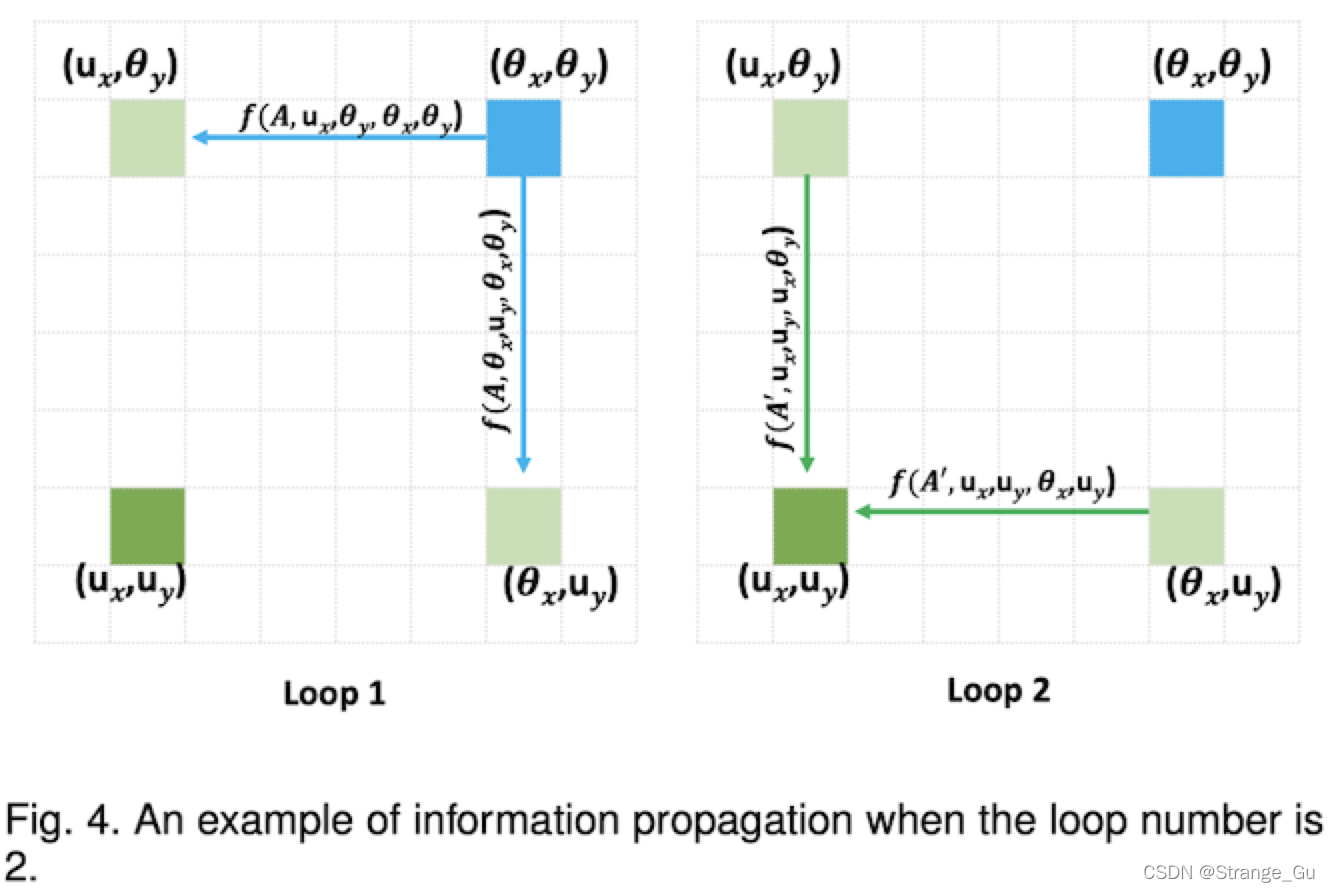
通过两次十字交叉注意力操作后,特征图中每个特征点与所有特征点的相关程度的信息传递的过程如图4所示。
2.3.1 如左图所示,经过第一个十字交叉注意力操作后,特征点 ( θ x , θ y ) (\theta_x, \theta_y) (θx,θy)只能计算与其水平和竖直方向上的特征(如图中 ( u x , θ y ) (u_x, \theta_y) (ux,θy)和 ( θ x , u y ) (\theta_x,u_y) (θx,uy))间的相关程度,将 ( θ x , θ y ) (\theta_x, \theta_y) (θx,θy)的信息传递给两者,此时无法计算和 ( u x , u y ) (u_x,u_y) (ux,uy)的相关程度。
2.3.2 如右图所示, ( u x , θ y ) (u_x, \theta_y) (ux,θy)和 ( θ x , u y ) (\theta_x,u_y) (θx,uy)是在 ( u x , u y ) (u_x, u_y) (ux,uy)的十字交叉路径上,当经过第二个十字交叉注意力操作后, ( u x , θ y ) (u_x, \theta_y) (ux,θy)和 ( θ x , u y ) (\theta_x,u_y) (θx,uy)即可各自把与 ( θ x , θ y ) (\theta_x, \theta_y) (θx,θy)的相关程度信息传递给 ( u x , u y ) (u_x,u_y) (ux,uy)。
综上,RCCA模块弥补了一次十字交叉注意力操作不能从所有像素中获得密集的上下文信息的缺陷。
3. Code
3.1 十字交叉注意力模块中要计算某像素与其水平和竖直方向上所有元素的相关程度。将降通道后的自注意力中的特征图 Q u e r y ( B , C ′ , H , W ) Query^{(B,C^{'},H,W)} Query(B,C′,H,W)和特征图 K e y ( B , C ′ , H , W ) Key^{(B,C^{'},H,W)} Key(B,C′,H,W)分别沿水平方向 W W W和竖直方向 H H H计算水平方向和竖直方向上的相关程度。
3.2 比如在特征图 Q u e r y ( B , C ′ , H , W ) Query^{(B,C^{'},H,W)} Query(B,C′,H,W)中,一共 B B B个 b a t c h batch batch,每个 b a t c h batch batch中都有 H × W H \times W H×W个 C ′ C^{'} C′维特征。考虑将特征图 Q u e r y ( B , C ′ , H , W ) Query^{(B,C^{'},H,W)} Query(B,C′,H,W)表示成 ( B × W , H , C ′ ) (B \times W, H, C^{'}) (B×W,H,C′)维矩阵后,表示一共有 B × W B \times W B×W个 b a t c h batch batch,每个 b a t c h batch batch中都有 H H H个 C ′ C^{'} C′维特征,即是 H × C ′ H \times C^{'} H×C′维矩阵。
3.3 同上,将特征图 K e y ( B , C ′ , H , W ) Key^{(B,C^{'},H,W)} Key(B,C′,H,W)转换成 ( B × W , C ′ , H ) (B \times W, C^{'},H) (B×W,C′,H)维矩阵。
3.4 当计算竖直方向上所有像素的相关程度时, t o r c h . b m m ( Q u e r y ( B × W , H , C ′ ) , K e y ( B × W , C ′ , H ) ) torch.bmm(Query^{(B \times W,H,C^{'})},Key^{(B \times W, C^{'},H)}) torch.bmm(Query(B×W,H,C′),Key(B×W,C′,H))得到 A t t e n t i o n _ H ( B × W , H , H ) Attention\_H^{(B \times W, H,H)} Attention_H(B×W,H,H)。这样就在特征图每行分开后,计算出每个像素与沿着竖直方向上像素的相关程度。
3.5 按照类似3.2-3.4思路即可计算出沿水平方向上的相关程度 A t t e n t i o n _ W ( B × H , W , W ) Attention\_W^{(B \times H,W,W)} Attention_W(B×H,W,W)。
3.6 将
A
t
t
e
n
t
i
o
n
_
H
(
B
×
W
,
H
,
H
)
Attention\_H^{(B \times W, H,H)}
Attention_H(B×W,H,H)转换成
A
t
t
e
n
t
i
o
n
_
H
(
B
,
H
,
W
,
H
)
Attention\_H^{(B,H,W,H)}
Attention_H(B,H,W,H)后,去掉像素与自己的相关程度。再将
A
t
t
e
n
t
i
o
n
_
W
(
B
×
H
,
W
,
W
)
Attention\_W^{(B \times H,W,W)}
Attention_W(B×H,W,W)转换成
A
t
t
e
n
t
i
o
n
_
W
(
B
,
H
,
W
,
W
)
Attention\_W^{(B,H,W,W)}
Attention_W(B,H,W,W)后,再在
d
i
m
=
3
dim=3
dim=3上进行
c
o
n
c
a
t
e
n
a
t
e
concatenate
concatenate操作和
s
o
f
t
m
a
x
softmax
softmax操作,即得到特征图上沿着十字交叉路径上的注意力分数。
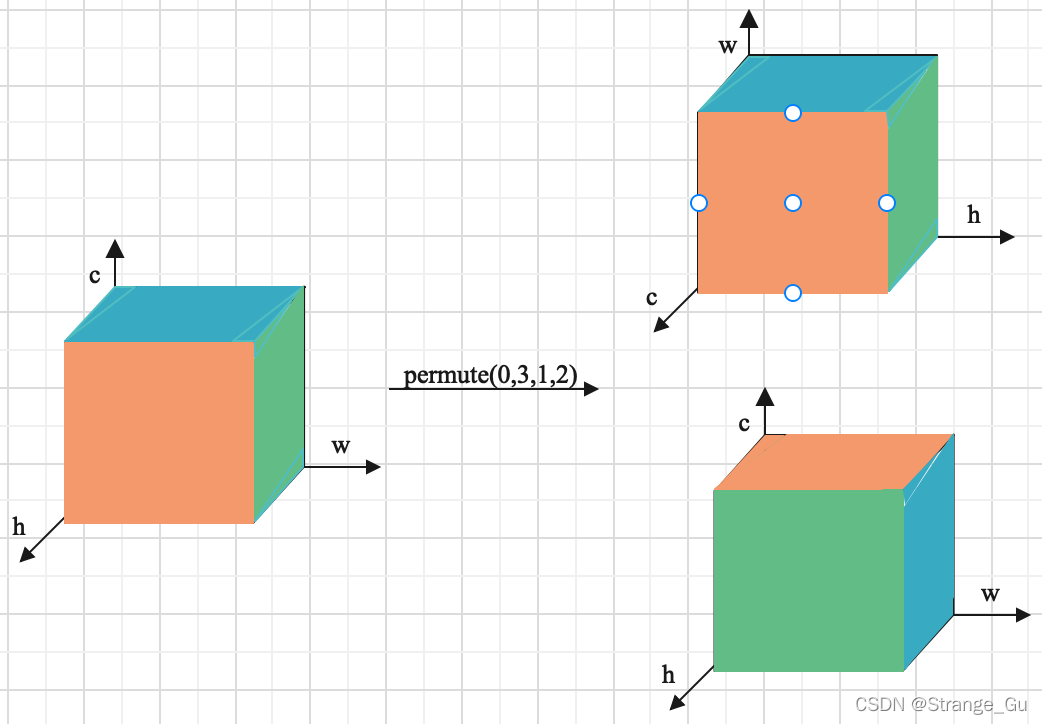
注:torch.permute()操作在二维矩阵上进行转置,行变列,列变成行的过程。在三维矩阵上操作也如同二维矩阵上效果一样,是在换坐标轴,但理解起来困难,故配一张图(图中batch=1)帮助理解torch.permute()操作对数据的变换过程,先看图右上方,数据位置不动,将坐标轴位置对应变换;再如右下图,再以之前的坐标轴方向去查看数据。torch.permute()大概就是这样对数据进行了变换。
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn import Softmax
def INF(B, H, W):
return -torch.diag(torch.tensor(float("inf")).repeat(H), 0).unsqueeze(0).repeat(B*W, 1, 1)
class CrissCrossAttention(nn.Module):
"""Criss-Cross Attention Moudle"""
def __init__(self, in_dim):
super(CrissCrossAttention, self).__init__()
self.query_conv = nn.Conv2d(in_channels=in_dim, out_channels=in_dim//8, kernel_size=1)
self.key_conv = nn.Conv2d(in_channels=in_dim, out_channels=in_dim//8, kernel_size=1)
self.value_conv = nn.Conv2d(in_channels=in_dim, out_channels=in_dim, kernel_size=1)
self.softmax = Softmax(dim=3)
self.INF = INF
self.gamma = nn.Parameter(torch.zeros(1))
def forward(self, x):
m_batchsize, _, height, width = x.size()
proj_query = self.query_conv(x)
# b, c', h, w ===> b, w, c', h ===> b*w, c', h ===> b*w, h, c'
proj_query_H = proj_query.permute(0, 3, 1, 2).contiguous().view(m_batchsize*width, -1, height).permute(0, 2, 1)
# b, c', h, w ===> b, h, c', w ===> b*h, c', w ===> b*h, w, c'
proj_query_W = proj_query.permute(0, 2, 1, 3).contiguous().view(m_batchsize*height, -1, width).permute(0, 2, 1)
proj_key = self.key_conv(x)
# b, c', h, w ===> b, w, c', h ===> b*w, c', h
proj_key_H = proj_key.permute(0, 3, 1, 2).contiguous().view(m_batchsize*width, -1, height)
# b, c', h, w ===> b, h, c', w ===> b*h, c', w
proj_key_W = proj_key.permute(0, 2, 1, 3).contiguous().view(m_batchsize*height, -1, width)
proj_value = self.value_conv(x)
# b, c', h, w ===> b, w, c', h ===> b*w, c', h
proj_value_H = proj_value.permute(0, 3, 1, 2).contiguous().view(m_batchsize*width, -1, height)
# b, c', h, w ===> b, h, c', w ===> b*h, c', w
proj_value_W = proj_value.permute(0, 2, 1, 3).contiguous().view(m_batchsize*height, -1, width)
# torch.bmm((b*w,h,c')x(b*w,c',h))===>(b*w,h,h)+(b*w,h,h)===>(b*w,h,h)===>(b,w,h,h)===>(b, h, w, h)
energy_H = (torch.bmm(proj_query_H, proj_key_H)+self.INF(m_batchsize, height, width)).view(m_batchsize, width, height, height).permute(0, 2, 1, 3)
# torch.bmm((b*h,w,c')x(b*h,c',w))===>(b*h,w,w)===>(b, h, w, w)
energy_W = (torch.bmm(proj_query_W, proj_key_W)).view(m_batchsize, height, width, width)
# torch.cat([(b,h,w,h),(b,h,w,w)], 3)===>(b,h,w,h+w)
concate = self.softmax(torch.cat([energy_H, energy_W], 3))
# (b,h,w,h+w)===>(b,h,w,h)===>(b,w,h,h)===>(b*w,h,h)
att_H = concate[:,:,:,0:height].permute(0, 2, 1, 3).contiguous().view(m_batchsize*width, height, height)
# (b,h,w,h+w)===>(b,h,w,w)===>(b*h,w,w)
att_W = concate[:,:,:,height:height+width].contiguous().view(m_batchsize*height, width, width)
# torch.bmm((b*w,c',h)x(b*w,h,h))===>(b*w,c',h)===>(b,w,c',h)===>(b,c',h,w)
out_H = torch.bmm(proj_value_H, att_H.permute(0, 2, 1)).view(m_batchsize, width, -1, height).permute(0, 2, 3, 1)
# torch.bmm((b*h,c',w)x(b*h,w,w))===>(b*h,c',w)===>(b,h,c',w)===>(b,c',h,w)
out_W = torch.bmm(proj_value_W, att_W.permute(0, 2, 1)).view(m_batchsize, height, -1, width).permute(0, 2, 1, 3)
return self.gamma*(out_H + out_W) + x