数据加密标准(DES)
1973年,美国NBS向全世界征集 Data Encryption Standard(DES,数据加密标准),由IBM研究的DES算法于1977年得到美国政府的正式许可,并成为了第一代公开的、完全说明细节的商业级密码标准,尽管DES注定会被Advanced Encryption Standard(AES,高级加密标准)代替,但DES作为经典的对称密码,仍然对于之后学习其他对称密码有很重要的借鉴意义。
更新历史:
- 2021年07月25日完成初稿
1. 传统分组密码结构
前述讨论过传统密码的分类,根据不同的标准将密码分为了以下几类:
- 根据使用的技术:代替密码、置换密码和乘积密码
- 根据加密时明文长度:分组密码和流密码
- 根据使用密钥个数:对称密码和公钥密码
对于对称密码而言,根据之前的讨论,单纯的代替密码、置换密码都是不安全的,因此经典的对称密码同时使用了两种技术,而对于分组密码和流密码的取舍是值得进一步分析的。
1.1 分组密码
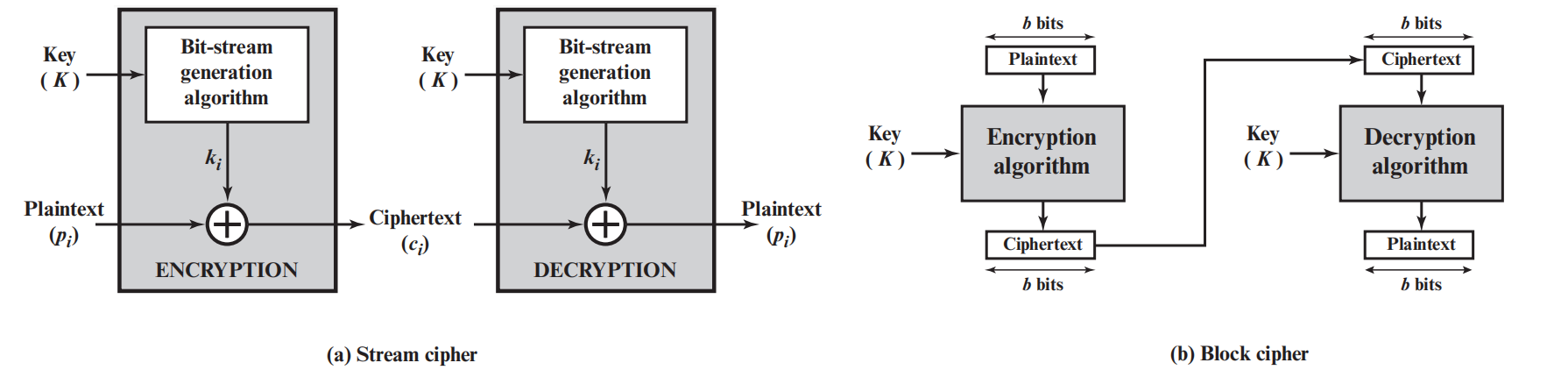
流密码(Stream cipher)对明文进行加密时,每次处理明文的一个元素(通常 1 1 1比特或者 1 1 1字节),而分组密码(Block cipher)对明文进行加密时,每次处理明文的一组元素(通常 64 64 64比特、 128 128 128比特等),如下图所示:
左图是流密码,其每次加密和解密一个比特,而右图是分组密码(块密码),其每次加密和解密 b b b个比特,通常 b b b为 64 , 128 , 256 64,128,256 64,128,256等。不过需要注意的是,这两者的区别并不是加密和解密的比特数的区别,其区别在于:流密码的一位密文 c i c_i ci只取决于一位明文 p i p_i pi,而分组密码的密文分组中的任何一个 c i c_i ci,都取决于 b b b比特的明文分组中的所有 p p p,因此分组密码中每一位明文都尽可能多地影响则密文的结果。
因此分组密码在一定程度上是优于流密码的,但并不是所有分组密码都有这样的效果,因为取决于分组密码的工作模式(后续文章会具体讲述),在一些分组密码的工作模式下,分组密码可以达到流密码的效果。因此大多数对称密码就是对称分组密码,并且使用了代替和置换两种技术,下面讲述的Feistel密码结构就是这样的一种密码体系。
1.2 Feistel密码结构
正如其名称一样,Feistel密码结构并不是一种具体的密码算法,更像是一种密码结构。对于密码设计人员而言,它们一直追求一种理想分组密码体制,但由于其并不容易实现,因此物理学家兼密码学家Horst Feistel在IBM工作时提出用乘积密码的概念来逼近理想分组密码。下面首先介绍理想分组密码的设计及其局限性,以及详细介绍Feistel结构,Feistel密码结构是DES的基础。
1.2.1 理想分组密码
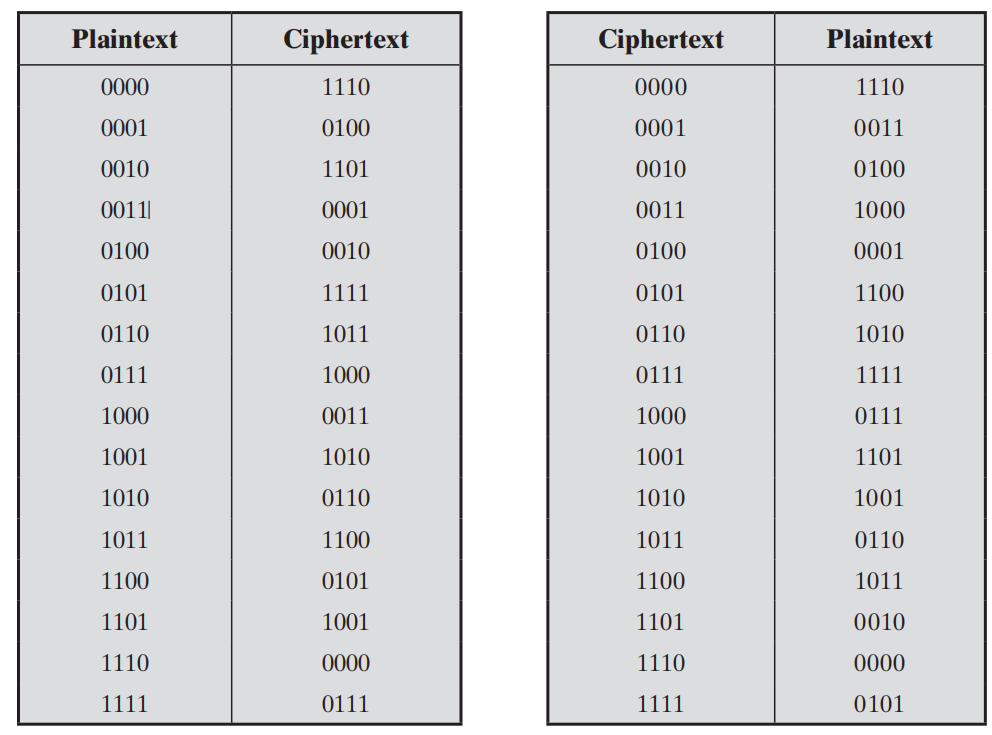
假设分组密码作用与 n n n位明文分组,并产生 n n n位密文分组,则明文空间 M M M的大小 ∣ M ∣ = 2 n |M|=2^n ∣M∣=2n,密文空间 C C C大小为 ∣ C ∣ = 2 n |C|=2^n ∣C∣=2n,因此加密过程就是从明文空间到密文空间的映射,解密过程就是从密文空间到明文空间的映射,为了加密过程和解密过程是可逆的,因此映射都是可逆映射。根据之前的讨论,对于集合大小为 2 n 2^n 2n的映射,所有可逆映射的数目为 2 n ! 2^n! 2n!个,下面给出了分组规模 n = 4 n=4 n=4时的普通代替密码的变换:
当分组规模 n n n太小时,密码系统等价于一个简单的代替密码,用明文的分析统计方法是很容易进行攻击的,当这仅仅是因为分组规模太小,只有分组规模足够大时才能将明文的统计特征覆盖以抵御频率分析攻击。当分组规模太大时,密钥的传输成为了问题,对于分组大小为 4 4 4的密码系统而言,需要存储上图中的变换表(左表或者右表中的第二列),比如需要存储明文转换为密文的变换表的键值对 [ 0000 : 1110 , . . . , 1111 : 0111 ] [0000:1110, ..., 1111:0111] [0000:1110,...,1111:0111],假如规定变换表的键的顺序是 0000 ∼ 1111 0000\sim 1111 0000∼1111,故只需要存储 [ 1110 , . . . , 0111 ] [1110,...,0111] [1110,...,0111]即可,因此需要存储 4 × 2 4 = 64 4\times 2^4=64 4×24=64比特的密钥,对于分组规模为n的情况,需要存储 n × 2 n n\times 2^n n×2n比特的密钥,如果分组大小是 64 64 64比特时,则总共存储的数据是 64 × 2 64 = 2 70 ≈ 1 0 21 64\times 2^{64}=2^{70}\approx 10^{21} 64×264=270≈1021比特,这显然是不合理的。
Feistel对于分组规模 n n n进行了权衡,提出了保持分组长度仍为 n n n比特,但减少使用可逆映射的个数,即不再使用 2 n ! 2^n! 2n!个可逆映射,而采用 k k k比特的密钥,仅仅使用 2 k 2^k 2k个变换,这样的变换是可以找到的,只需要取可逆映射的子集即可,下面就具体阐述Feistel密码结构的思想和具体结构。
1.2.2 混淆和扩散
Feistel结构用乘积密码的概念来逼近理想分组密码,乘积密码同时使用了之前讨论的代替和置换技术:
- 代替:每个明文字符被唯一地替换为相应的密文字符
- 置换:明文字符序列被替换为该序列的一个置换
实际上,Feistel结构使用的代替和置换技术源自于Shannon提出的混淆和扩散原则。混淆和扩散原则是分组密码中极为重要的两条原则,下面来阐述一些混淆和扩散原则的作用。
对于攻击者而言,他们拥有密文,通过分析可以得到一些关于明文的特性(如统计特性),因此攻击者可以针对此去破解对应明文或是分析得出密钥,而Shannon提出可以利用混淆和扩散来保护明文和密钥以增加其抗攻击能力:
- 扩散:使明文的统计特征消散在密文中,以阻止攻击者从密文解密到明文
- 混淆:尽可能使得密文和密钥之间的关系变得复杂,以阻止攻击者从密文恢复到密钥
对于扩散,可以通过让每个明文字符尽可能多地影响密文字符可以实现这一点,分组密码的一些工作模式可以达到这样的效果。而对于混淆而言,可以通过一些复杂的代替算法来实现。混淆和扩散是设计分组密码的本质,如果分组密码并不能很好地实现混淆和扩散,那么其和流密码是没有本质区别的,下面的Feistel密码结构就很好地说明了这一点
1.2.3 Feistel结构
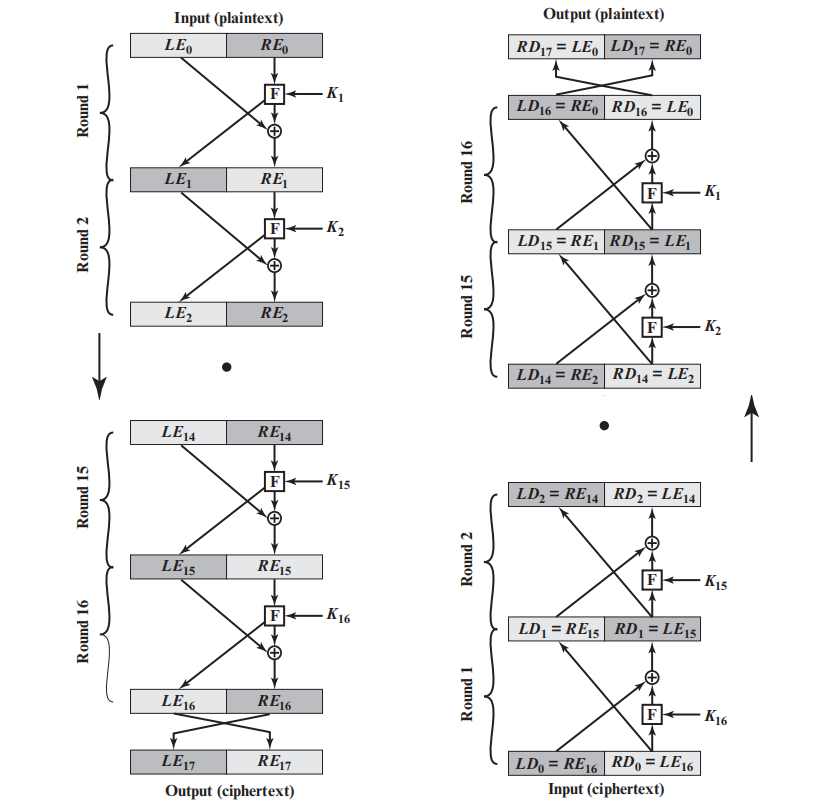
下图是Feistel结构的加密和解密的示意图。对于加密而言,输入是 2 w 2w 2w比特长度的明文分组和密钥 K K K,初始时将明文分组分成等长的左右两个部分 L E 0 LE_0 LE0和 R E 0 RE_0 RE0,该分组经过 n n n轮迭代后(这里是 16 16 16轮)得到密文分组。
在第 i i i轮,其输入是上一轮的输出 L E i − 1 LE_{i-1} LEi−1、 R E i − 1 RE_{i-1} REi−1和子密钥 K i K_i Ki(由密钥 K K K推导而来),经过加密变换
L E i = R E i − 1 , R E i = L E i − 1 ⊕ F ( R E i − 1 , K i ) (1.1) LE_i=RE_{i-1},\quad RE_i = LE_{i-1}\oplus F(RE_{i-1},K_i)\tag{1.1} LEi=REi−1,REi=LEi−1⊕F(REi−1,Ki)(1.1)
从而获得输出 L E i LE_i LEi、 R E i RE_i REi,它们将作为第 i + 1 i+1 i+1轮的输入。而对于解密过程,初始输入为,然后经过解密变换:
L D i = R D i − 1 , R D i = L D i − 1 ⊕ F ( R D i − 1 , K 16 − i + 1 ) (1.2) LD_i=RD_{i-1},\quad RD_i = LD_{i-1}\oplus F(RD_{i-1},K_{16-i+1})\tag{1.2} LDi=RDi−1,RDi=LDi−1⊕F(RDi−1,K16−i+1)(1.2)
最终输出明文。加密过程和解密过程是联系紧密的,可以证明有下面的关系:
L D i = R E 16 − i , R D i = L E 16 − i (1.3) LD_i=RE_{16-i},\quad RD_i=LE_{16-i}\tag{1.3} LDi=RE16−i,RDi=LE16−i(1.3)
总体来说,Feistel结构的具体实现依赖于以下参数和特征:
- 分组长度:分组长度越长,扩散的效果越好,安全性越高,但会使得加密解密变得困难,在DES中采用了 64 64 64位明文分组,而在AES中采用了 128 128 128位明文分组
- 密钥长度:密钥长度越长,抗穷尽攻击能力更强,混淆性更好,因此安全性也越好,但会降低加密和解密速度,通常采用 128 128 128位密钥长度甚至更长
- 迭代轮数:多轮加密可以使得算法变得更加复杂,从而获得更高的安全性,一般是 16 16 16轮
- 子密钥生成算法和轮函数:越复杂越好,抗密码攻击能力越强
2. 数据加密标准
下面将介绍经典的对称密码——数据加密标准(Data Encryption Standard, DES),它和高级加密标准AES是使用最为广泛的对称密码体制,尽管DES在可预见的将来将被AES替代,但DES中蕴含的基本思想是十分值得学习的。
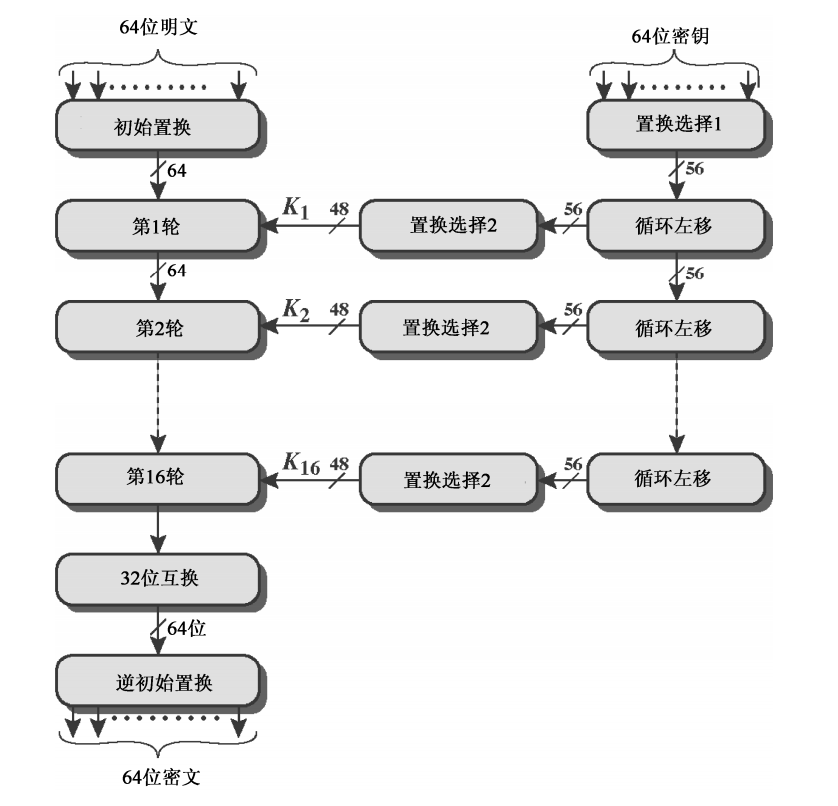
DES算法的主要流程如下图。DES加密算法每次处理64位明文分组,主要需要经过下面几个步骤:
- 初始置换:将明文按照初始置换表进行置换操作
- 16轮加密操作:将明文分成左右两个部分 L i − 1 , R i − 1 L_{i-1}, R_{i-1} Li−1,Ri−1,利用密钥 K i K_i Ki,生成下一轮的输出 L i L_i Li和 R i R_i Ri,每一轮加密过程都有代替和置换的作用
- 32位互换:将加密过程的第 16 16 16轮的输出 L 16 L_{16} L16和 R 16 R_{16} R16实现互换以便更好地实施解密过程
- 逆初始置换:最后对
32
32
32位互换后的密文进行逆初始置换的操作,生出
64
64
64位密文,该过程是初始置换的逆过程
图2.1 DES加密算法概述
下面就以明文 p l a i n t e x t = 0 x 02468 a c e e c a 86420 plaintext = 0x02468aceeca86420 plaintext=0x02468aceeca86420,密钥 k e y = 0 x 0 f 1571 c 947 d 9 e 859 key =0x0f1571c947d9e859 key=0x0f1571c947d9e859为例详细介绍DES加密的具体细节。
2.1 初始置换和逆初始置换
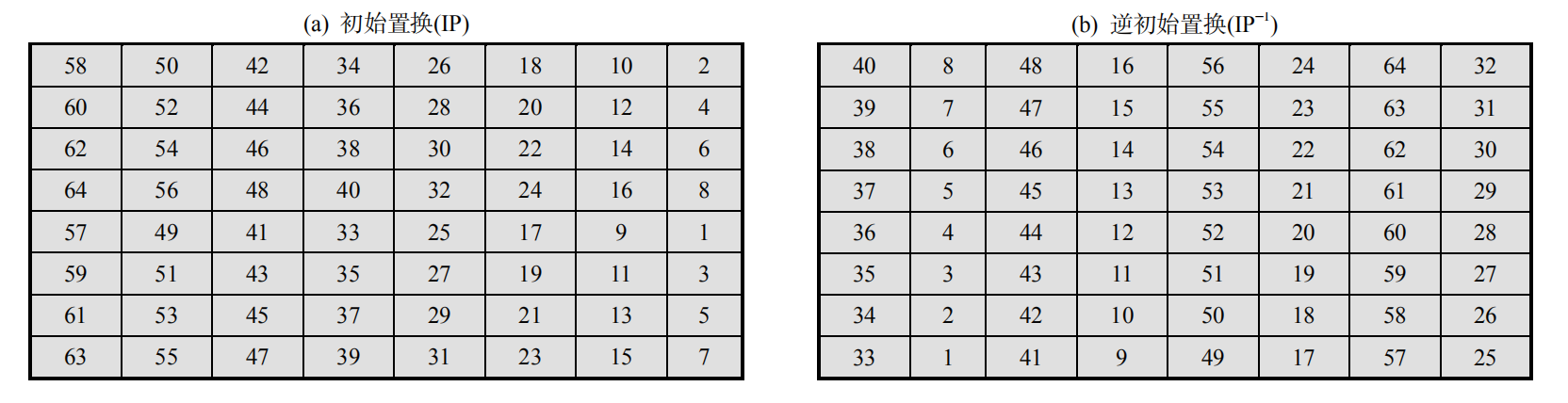
初始置换是将 64 64 64位的明文分组按照初始置换表进行置换运算,而逆初始置换表是将经过16轮加密和32位互换的分组按照逆初始置换表进行置换运算。下图就是本例使用的初始置换表(Initial Permutation Table)和逆初始置换表。
来观察一下初始置换(IP)的情况,其是 8 × 8 8\times 8 8×8的矩阵,阅读矩阵的顺序是从左至右,从上到下(即按行读取),第一行中的 ( 58 , 50 , 42 , 34 , 26 , 18 , 10 , 2 ) (58,50,42,34,26,18,10,2) (58,50,42,34,26,18,10,2)表示将初始的明文 p l a i n t e x t = 0 x 02468 a c e e c a 86420 plaintext = 0x02468aceeca86420 plaintext=0x02468aceeca86420的二进制表示中第 58 , 50 , 42 , 34 , 26 , 18 , 10 , 2 58,50,42,34,26,18,10,2 58,50,42,34,26,18,10,2位(编号从 1 1 1开始)放置到该位置,其余行以此类推,从左至右,从上到下(即按行读取)组成置换后的明文(第 1 1 1行第 1 1 1列在最高位,第 8 8 8行第 8 8 8列在最低位)。
对于 p l a i n t e x t = 0 x 02468 a c e e c a 86420 plaintext = 0x02468aceeca86420 plaintext=0x02468aceeca86420,其二进制表示是 64 64 64位,其第 58 , 50 , 42 , 34 , 26 , 18 , 10 , 2 58,50,42,34,26,18,10,2 58,50,42,34,26,18,10,2位是 ( 0 , 1 , 0 , 1 , 1 , 0 , 1 , 0 ) (0,1,0,1,1,0,1,0) (0,1,0,1,1,0,1,0),因此置换后的最高位的一个字节应该为 0 x 5 a 0x5a 0x5a。而实际上plaintext经过初始置换的结果是 I P ( p l a i n t e x t ) = 0 x 5 a 005 a 003 c f 03 c 0 f IP(plaintext)=0x5a005a003cf03c0f IP(plaintext)=0x5a005a003cf03c0f,因此是相符合的。
另一个值得关注的是否有关系式 I P − 1 ( I P ( p i ) ) = p i IP^{-1}(IP(p_i))=p_i IP−1(IP(pi))=pi,直观上看,对于明文而言,初始置换时其第 58 58 58位被放到了第 1 1 1行第 1 1 1列(即置换后明文的第 1 1 1位),而初始置换后明文的第一位放到了第 58 58 58位(观察逆初始置换表中 1 1 1的位置发现其在第 8 8 8行第 2 2 2列,即编号为 58 58 58的位置),因此两次置换下来是回到了初始位置的,其他位也是如此。
2.2 16轮加密
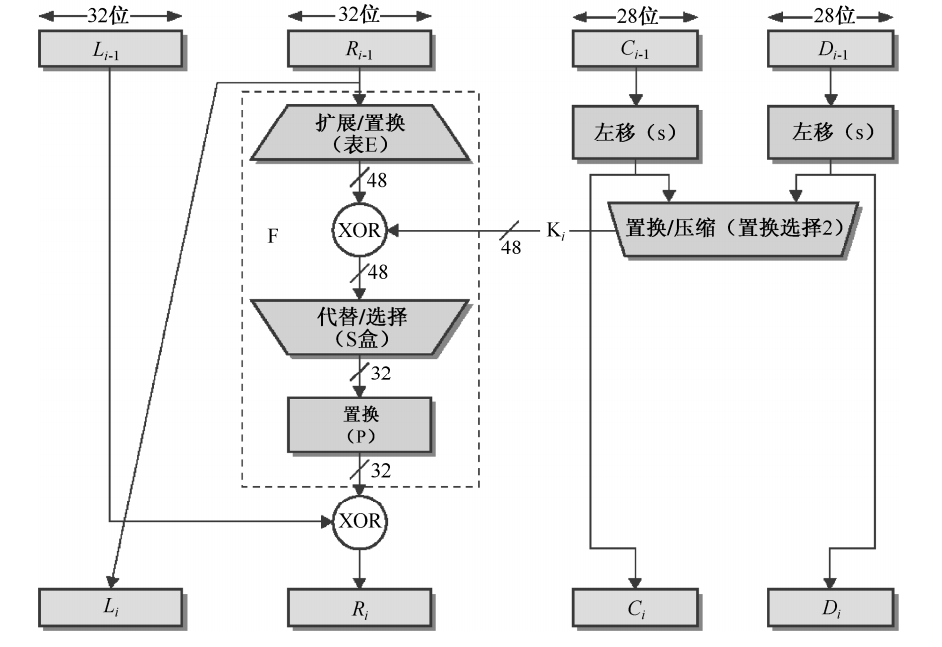
16 16 16轮加密是DES的重点,由于 16 16 16轮加密过程都是相同的,因此只需要关注一轮加密的过程。下面是第i轮加密过程中明文和密钥的处理过程。每一轮的输入都是左右两个部分 L i − 1 L_{i-1} Li−1和 R i − 1 R_{i-1} Ri−1,利用密钥 K i K_i Ki通过下面的加密变换
L i = R i − 1 R i = L i − 1 ⊕ F ( R i − 1 , K i ) L_i=R_{i-1}\\ R_i=L_{i-1}\oplus F(R_{i-1}, K_i) Li=Ri−1Ri=Li−1⊕F(Ri−1,Ki)
其中有两点是值得讨论的:
- 轮函数 F F F
- 子密钥生成函数
图2.3 DES一轮加密
2.2.1 DES轮函数
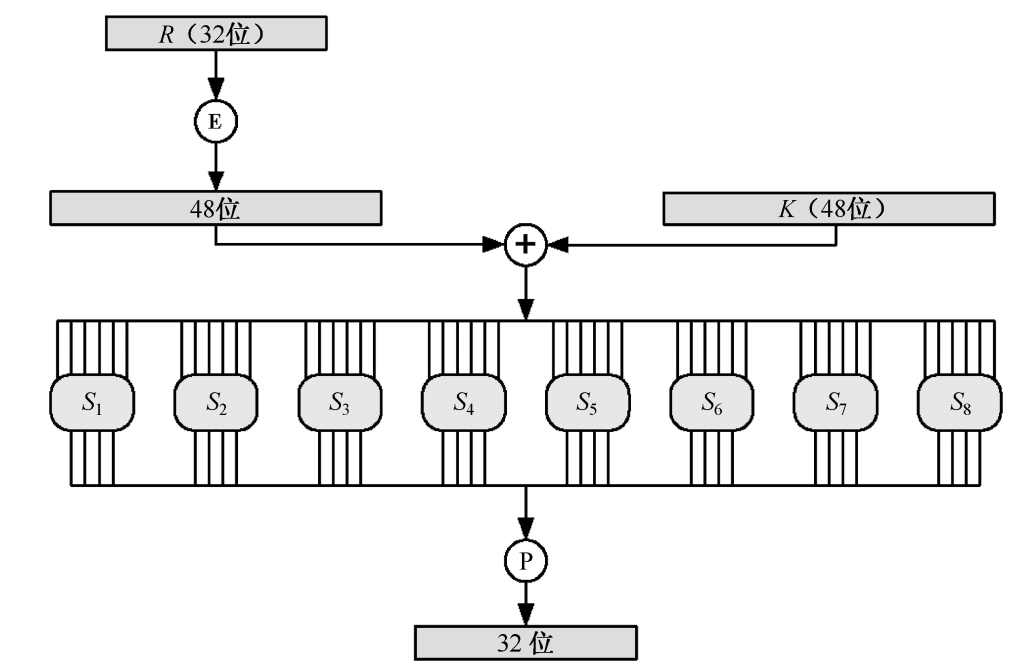
由上图可知,轮函数主要经历四个过程:
- 扩展置换:将 32 32 32比特的 R i − 1 R_{i-1} Ri−1经过扩展置换生成 48 48 48比特的数据,记为 R E R_E RE
- 异或运算: R E R_E RE与 K i K_i Ki进行异或运算 R E ⊕ K i R_E\oplus K_i RE⊕Ki
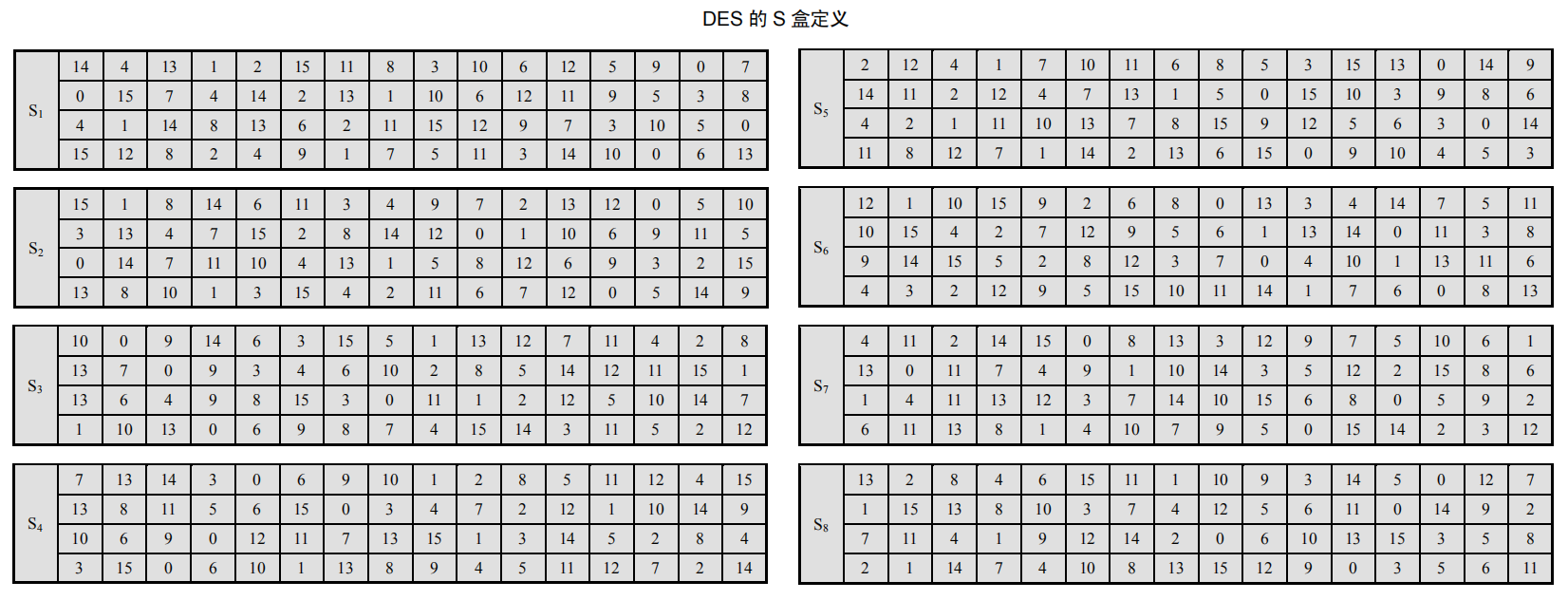
- 代替选择:利用 S S S盒从异或运算的结果( 48 48 48比特)中选出 32 32 32位的数据,记为 R S R_S RS
- 置换:最后 R S R_S RS经过置换运算生成 R P R_P RP,该 R P R_P RP应与 L i − 1 L_{i-1} Li−1异或生成 R i R_i Ri
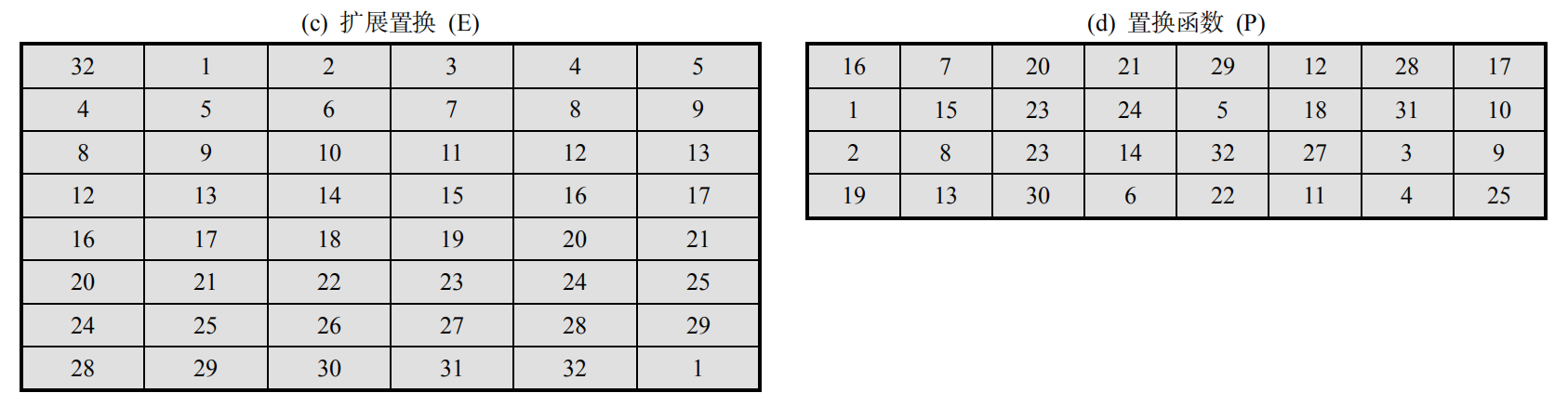
其中,扩展置换的表 E E E和置换表 P P P如下,这里的置换函数和上面介绍的置换是一致的,没有本质的区别。对于扩展置换事实上就是用 32 32 32比特的数据重复了其中 16 16 16比特组合形成了 48 48 48比特,其重复的规则是对于表 E E E而言,第二列减去 1 1 1得到第一列( 1 − 1 = 0 1-1=0 1−1=0,用 32 32 32表示),第五列加 1 1 1得到第六列( 32 + 1 = 33 32+1=33 32+1=33,用 1 1 1表示)。
步骤 2 2 2中的异或运算是十分简单的,需要讨论代替选择的过程,记 R E ⊕ K i = R ⊕ R_E\oplus K_i=R_{\oplus} RE⊕Ki=R⊕, R ⊕ R_{\oplus} R⊕是 48 48 48比特,分成 8 8 8组,每组 6 6 6比特,设为 r 5 r 4 r 3 r 2 r 1 r 0 r_5r_4r_3r_2r_1r_0 r5r4r3r2r1r0,其中 r 5 r 0 r_5r_0 r5r0构成行数 r r r, r 4 r 3 r 2 r 1 r_4r_3r_2r_1 r4r3r2r1构成列 c c c,之后将 ( r , c ) (r,c) (r,c)查表获得 4 4 4比特的数据,从而 8 8 8组共获得 32 32 32比特。下面是异或运算和S盒的具体细节。
2.2.2 子密钥生成函数
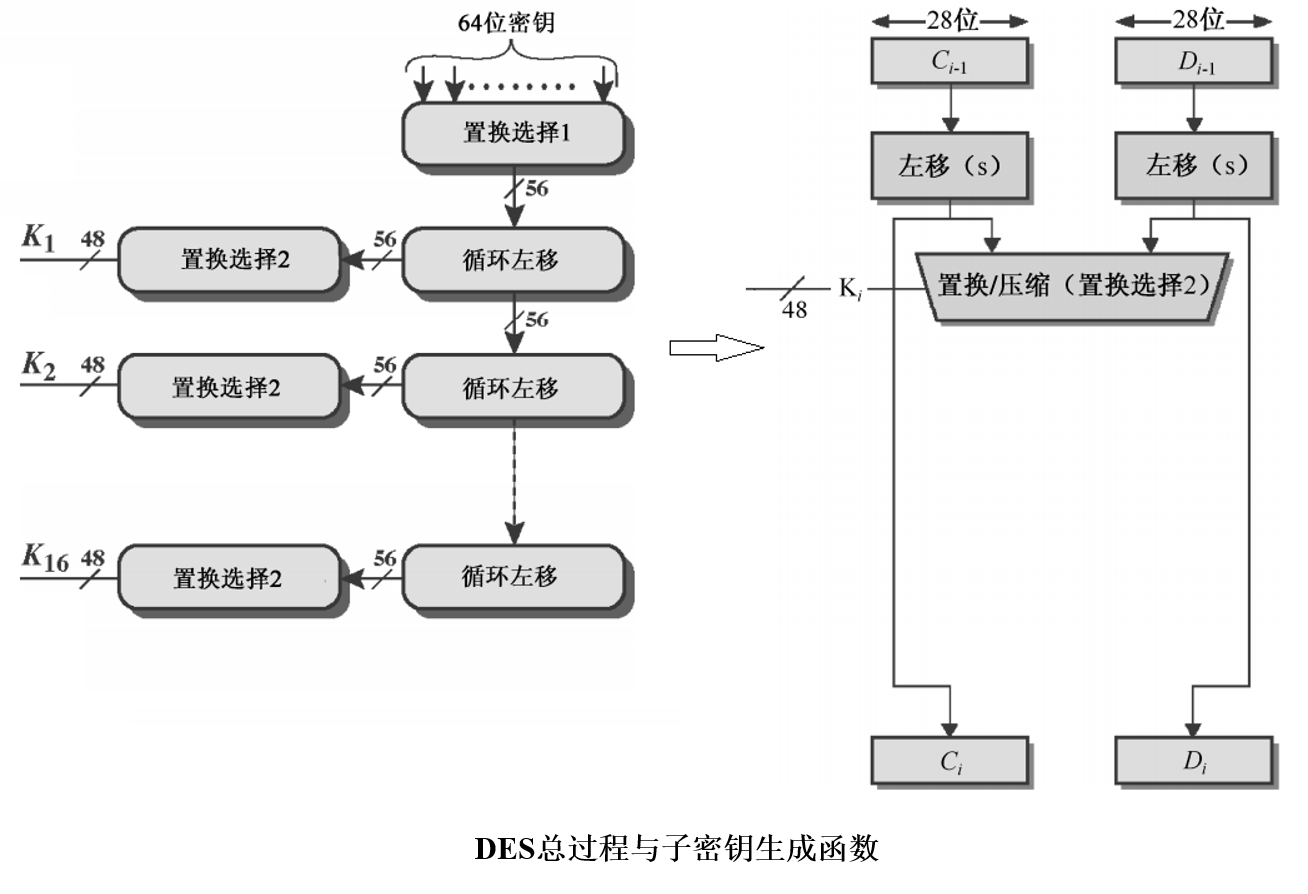
密钥一开始是 64 64 64比特,但其中只有 56 56 56比特起作用,首先密钥要经过第一轮的置换选择 1 1 1,置换选择 1 1 1会选择密钥中的 56 56 56比特等分形成 28 28 28比特的 ( C 0 , D 0 ) (C_0,D_0) (C0,D0)。
在子密钥生成函数中,每一轮中的密钥 ( C i − 1 , D i − 1 ) (C_{i-1},D_{i-1}) (Ci−1,Di−1)会先进行左移运算,然后通过置换选择 2 2 2,选出 48 48 48比特作为该轮的密钥 K i K_i Ki,而下轮的密钥则是左移过的密钥(未经过置换选择),如下图所示。
下表本例中的初始密钥和置换选择的置换表,值得一提的是子密钥生成函数中的左移次数每一轮是不一样的,而且总移位次数为 28 28 28位。
2.2.3 一轮加密的示例
明文 p l a i n t e x t = 0 x 02468 a c e e c a 86420 plaintext = 0x02468aceeca86420 plaintext=0x02468aceeca86420,密钥 k e y = 0 x 0 f 1571 c 947 d 9 e 859 key = 0x0f1571c947d9e859 key=0x0f1571c947d9e859,之前叙述了初始置换后(置换表见图2.2)有 I P ( p l a i n t e x t ) = 0 x 5 a 005 a 003 c f 03 c 0 f IP(plaintext)=0x5a005a003cf03c0f IP(plaintext)=0x5a005a003cf03c0f,故 L 0 = 0 x 5 a 005 a 00 L_0=0x5a005a00 L0=0x5a005a00, R 0 = 0 x 3 c f 03 c 0 f R_0=0x3cf03c0f R0=0x3cf03c0f,这是第一轮的输入,讨论如何产生第一轮的输出:
根据
L
i
=
R
i
−
1
,
R
i
=
L
i
−
1
⊕
F
(
R
i
−
1
,
K
i
)
L_i=R_{i-1},R_i=L_{i-1}\oplus F(R_{i-1}, K_i)
Li=Ri−1,Ri=Li−1⊕F(Ri−1,Ki),故第一轮的输出有:
L
1
=
R
0
=
0
x
3
c
f
03
c
0
f
R
1
=
0
x
5
a
005
a
00
⊕
F
(
0
x
3
c
f
03
c
0
f
,
K
1
)
L_1=R_0=0x3cf03c0f\\ R_1=0x5a005a00\oplus F(0x3cf03c0f, K_1)
L1=R0=0x3cf03c0fR1=0x5a005a00⊕F(0x3cf03c0f,K1)
对于轮函数有:首先
R
0
R_0
R0经过扩展置换(扩展置换表见图2.4)可以得到
R
E
=
0
x
9
f
97
a
01
f
805
e
R_E=0x9f97a01f805e
RE=0x9f97a01f805e,之后其与轮密钥
K
i
K_i
Ki异或,因此下面需要求解
K
i
K_i
Ki:
初始密钥 k e y = 0 x 0 f 1571 c 947 d 9 e 859 key = 0x0f1571c947d9e859 key=0x0f1571c947d9e859,首先其需要经过图2.8的置换选择一(PC-1),从 64 64 64比特中选出 56 56 56比特,并将其等分为左右部分生成初始轮密钥 C 0 = 0 x 68 f c 44 a , D 0 = 0 x 1113 e 96 C_0=0x68fc44a,D_0=0x1113e96 C0=0x68fc44a,D0=0x1113e96,这是第一轮的初始轮密钥。查看图2.8的移位表(d),第一轮左移移位次数为 1 1 1,故得到左移移位后的轮密钥 C 0 = 0 x d 1 f 8894 , D 0 = 0 x 2227 d 2 c C_0=0xd1f8894,D_0=0x2227d2c C0=0xd1f8894,D0=0x2227d2c,则第一轮的轮密钥 K 1 = P C 2 ( C 0 ∣ ∣ D 0 ) = 0 x 7833 c 320 d a 70 K_1=PC_2(C_0||D_0)=0x7833c320da70 K1=PC2(C0∣∣D0)=0x7833c320da70,
故有 R E ⊕ K 1 = 0 x 9 f 97 a 01 f 805 e ⊕ 0 x 7833 c 320 d a 70 = 0 x e 7 a 4633 f 5 a 2 e = R ⊕ R_E\oplus K_1=0x9f97a01f805e\oplus 0x7833c320da70=0xe7a4633f5a2e=R_{\oplus} RE⊕K1=0x9f97a01f805e⊕0x7833c320da70=0xe7a4633f5a2e=R⊕。之后 R ⊕ R_{\oplus} R⊕需要经过S盒代替选择(根据图2.5代替选择过程和图2.6的S盒定义)得到 R S = 0 x a 32 f 11 c 2 R_S=0xa32f11c2 RS=0xa32f11c2,最后经过轮函数的置换(置换表见2.8的置换选择2)得到 R P = 0 x e 0 d 27245 R_P= 0xe0d27245 RP=0xe0d27245。
最后 R P R_P RP与 L 0 L_0 L0异或得到 R 1 = 0 x d c 224 e 4 a R_1=0xdc224e4a R1=0xdc224e4a,这就是第一轮完整的过程,之后 L 1 = 0 x 3 c f 03 c 0 f , R 1 = 0 x d c 224 e 4 a L_1=0x3cf03c0f,R_1=0xdc224e4a L1=0x3cf03c0f,R1=0xdc224e4a将作为第二轮的输入继续执行每一轮的加密。而解密过程是与加密过程相反的过程,在此不再赘述。
2.2 DES分析
DES算法其实还是比较简单,其主要的部分是轮函数和子密钥生成,每一轮的轮函数中输入64比特的明文,使用了扩展置换、代替选择和普通置换,最初输出64比特的密文,这些可以产生混淆和扩散的效果,下面分析一下DES抵御攻击的能力:
2.2.1 密钥和明文穷举攻击
由于DES有效的密钥有 56 56 56位,因此利用穷举攻击的话,将搜索 1 2 × 2 56 = 3.6 × 1 0 16 \frac{1}{2}\times 2^{56}=3.6\times 10^{16} 21×256=3.6×1016个密钥,若一台计算机每微秒执行一次解密,则需要 1.125 1.125 1.125年才能成功破解,这其实是不实际的。不过考虑多台计算机而言,解密时间将大大缩减,对于如今的超级计算机而言,只需要 1 1 1个小时就可以找到密钥,对此增加密钥位数是十分有效的策略,通过将密钥增加至 128 128 128比特,那么DES仍然是有效的,不过如今DES也有相应的替代算法,比如3DES、AES等。
如果不进行穷举攻击,而试图破解明文或者密钥,那么可以缩小密钥和明文的搜索空间,不过好在DES具有很强的雪崩效应:
- 雪崩效应:明文或者密钥的一位变化就可以引起密文的很多位发生变化
根据测试,改变明文或者密钥中的一位,最终大概密文改变的位数为 30 30 30比特左右,大概是密文位数 64 64 64比特的一半,而且经过三四轮函数加密后就达到这样的效果,这是十分好的性质,因为如果改变明文或者密钥中的一位而密文也不会改变太多位,那么攻击者可以针对这一点进行攻击
2.2.2 计时攻击和差分分析
计时攻击利用的事实是加密或解密算法对不同输入所花时间存在的细微的差别,对于DES而言,尽管不能证明DES可以抵御计时攻击,但直到目前为止计时攻击还未能很有效地攻击DES。
对于差分分析,差分分析时一种选择明文攻击,通过选择两条或多条不同的明文,这些明文只有特定位不同,然后观察密文,从而试图推测出密钥,但由于DES加密和解密有 16 16 16轮,因此差分分析事实上不能有效地攻击DES。
2.3 DES加密源代码
下面是DES加密算法的实现:
# plaintext = 0x02468aceeca86420
# key = 0x0f1571c947d9e859
# ciphertext = 0xda02ce3a89ecac3b
##################################################
# 使用的一些公共函数
# 输入:十六进制表示的数字data(如0x2f),转换后的位数n
# 输出:nbits的二进制字符串(如"00101111")
# 函数功能:将十六进制的数字转换为nbits的二进制字符串
def hex_to_binstr(data, n):
data = bin(data)[2:]
if n > len(data):
data = '0'*(n-len(data)) + data
return data
# 输入:二进制字符串(如"00101111")
# 输出:十六进制表示的数字(如0x2f),由于数字值不取决于进制,因此输出可能是实际整数值(如47)
# 函数功能:将二进制字符串("01...")转换十六进制的数字字符串(0x表示)
def binstr_to_hex(data):
return eval(hex(eval("0b" + str(data))))
# 输入:产生掩码的的位数N
# 输出:左掩码fff...f000...0(N个f,N个0),右掩码000...0fff...f(N个f,N个0)
# 函数功能:产生2N位的左掩码和右掩码(十六进制表示)
def mask(N):
lmask = eval("0b" + "1"*N + "0"*N)
rmask = eval("0b" + "0"*N + "1"*N)
return (lmask, rmask)
# 输入:置换表per_table,置换的数据data(一般是16进制或10进制整数值)
# 输出:置换后的数据值(一般是16进制或10进制整数值)
# 函数功能:实现数据的置换
def permutation(per_table, data):
data = hex_to_binstr(data, len(per_table)) # 将整数值转换为与置换表相同位数的二进制字符串
data_per = [data[per_table[i]-1] for i in range(len(per_table))] # 产生置换后的数据列表
return binstr_to_hex("".join(data_per))
# 输入:需要处理的数据data(一般是16进制),和分解的位数N(通常是data数据位数的一半)
# 输出:数据的前半部分和后半部分
# 函数功能:获得2N位数据的左N位部分和右N位部分(例如0x5a003cf0,前半部分是0x5a00,后半部分是0x3cf0)
def decomposition(data, N):
(lmask, rmask) = mask(N)
L = (data & lmask) >> N
R = data & rmask
return (L, R)
##################################################
# DES加密的一些函数
# 1.初始置换
# 输入:初始置换表IP和明文plaintext
# 输出:置换后的明文,并将其分解为左右部分,它们将是第一轮加密的输入
# 函数功能:DES初始置换操作
def DES_initial_permutation(IP, plaintext):
plaintext_per = permutation(IP, plaintext) # 数据置换
(L, R) = decomposition(plaintext_per, len(IP)//2) # 对置换后的数据进行分解成左右部分
return (L, R)
# 输入:密钥置换选择表PC_1和密钥key(64bits)
# 输出:置换选择之后的密钥key(56bits)
# 函数功能:DES对密钥初始置换选择操作
def DES_permutation_choice_key1(PC_1, key):
key = hex_to_binstr(key, 64) # 将密钥转换为64bits二进制字符串
key_per = [key[PC_1[i]-1] for i in range(len(PC_1))] # 产生置换后的数据列表
key_per = binstr_to_hex("".join(key_per))
(C, D) = decomposition(key_per, 28) # 对置换后的数据进行分解成左右部分
return (C, D)
# 2. 16轮加密
# 输入:扩展置换表per_table和数据data
# 输出:置换后的明文,并将其分解为左右部分,它们将是第一轮加密的输入
# 函数功能:DES每轮的扩展置换操作
def extend_permutation(per_table, data):
data = hex_to_binstr(data, 32) # 将整数值转换为与32bits二进制字符串,32bits是DES加密数据的一半长度
data_per = [data[per_table[i]-1] for i in range(len(per_table))] # 产生置换后的数据列表
return binstr_to_hex("".join(data_per))
# 输入:轮函数S盒roundfun_Sbox(可以看3维数组)和处理的数据
# 输出:经过S盒代替选择的数据
# 函数功能:数据为十六进制值,可扩展成48bits,分为8组,每组6bits(第0位和第5位结合起来称为行,其他位结合起来成为列)
# ,第i组数据在S盒的子盒Si(可看成二维数组)中查找数据,从而实现48bits->32bits
def SBOX_function(roundfun_Sbox, data):
data = hex_to_binstr(data, 48) # 将整数值转换为与48bits二进制字符串
data_list = [data[6*i:6*i+6] for i in range(8)]
data_sbox = "" # 经过S盒代替选择的数据
for i in range(len(data_list)):
r = eval("0b" + data_list[i][0] + data_list[i][5])
c = eval("0b" + data_list[i][1:5])
data_sbox += hex_to_binstr(roundfun_Sbox[i][r][c], 4)
return binstr_to_hex(data_sbox)
# 输入:第i轮的数据Ri_1,第i轮的密钥Ki,以及轮函数扩展置换表roundfun_E,S盒roundfun_Sbox和轮函数置换表roundfun_P
# 输出:轮函数F(Ri_1, Ki)的结果值
# 函数功能:DES中一轮的轮函数功能
def DES_round_function(i, Ri_1, Ki, roundfun_E, roundfun_Sbox, roundfun_P):
R_extend = extend_permutation(roundfun_E, Ri_1) # 扩展置换
R_sbox = SBOX_function(roundfun_Sbox, R_extend ^ Ki) # 利用S盒从异或运算的结果(48bits)中选出32bits的数据
R_sbox_per = permutation(roundfun_P, R_sbox) # 轮函数置换过程使用普通的置换函数即可
return R_sbox_per
# 输入:待移位的数据C,D和移位量rol_n
# 输出:移位后的数据
# 函数功能:对数据进行循环左移rol_n位
def rotate_left(C, D, rol_n):
C = hex_to_binstr(C, 28)
C = eval("0b" + C[rol_n:] + C[:rol_n])
D = hex_to_binstr(D, 28)
D = eval("0b" + D[rol_n:] + D[:rol_n])
return (C, D)
# 输入:密钥置换选择表PC_2和密钥Ki(56bits)
# 输出:置换选择之后的密钥Ki(48bits)
# 函数功能:DES对密钥每轮的置换选择
def DES_permutation_choice_key2(PC_2, Ki):
Ki = hex_to_binstr(Ki, 56) # 将密钥转换为64bits二进制字符串
Ki_per = [Ki[PC_2[i]-1] for i in range(len(PC_2))] # 产生置换后的数据列表
return binstr_to_hex("".join(Ki_per))
# 输入:第i轮的数据Li_1,Ri_1,第i轮的密钥Ki,以及轮函数扩展置换表roundfun_E,S盒roundfun_Sbox和轮函数置换表roundfun_P
# 输出:第i+1轮需要用到的输入Li, Ri
# 函数功能:DES加密一轮过程
def DES_encrypt_round(i, Li_1, Ri_1, Ci_1, Di_1, roundfun_E, roundfun_Sbox, roundfun_P, key_rol_number, PC_2):
(Ci, Di) = rotate_left(Ci_1, Di_1, key_rol_number[i]) # 循环左移key_rol_number[i]位
Ki = DES_permutation_choice_key2(PC_2, (Ci<<28) + Di) # 每轮对密钥的置换选择
Li = Ri_1
Ri = Li_1 ^ DES_round_function(i, Ri_1, Ki, roundfun_E, roundfun_Sbox, roundfun_P)
return(Li, Ri, Ci, Di)
# 3. 32位互换
# 函数功能:在16轮加密之后互换32位
def DES_exchange_32bits(Li, Ri):
return (Ri, Li)
# 4. 逆初始置换
# 函数功能:求置换IP的逆置换IP_inv
def invertible_permutation(IP):
dict_per = {} # 置换字典, 用于保持置换的对应关系
for i in range(len(IP)): # 生成置换字典
dict_per[IP[i]] = i+1
list_per = list(dict_per.items())
list_per.sort(key = lambda x:x[0])
IP_inv = [value for (key, value) in list_per]
return IP_inv
# 输入:初始置换表IP和明文plaintext
# 输出:置换后的密文ciphertext
# 函数功能:DES逆初始置换操作
def DES_invertible_initial_permutation(IP, text):
IP_inv = invertible_permutation(IP)
ciphertext = permutation(IP_inv, text)
return ciphertext
##################################################
# 主函数
# 明文和密钥
plaintext = 0x02468aceeca86420 # 64bits: 0000001001000110100010101100111011101100101010000110010000100000
key = 0x0f1571c947d9e859 # 64bits: 0000111100010101011100011100100101000111110110011110100001011001
# 初始置换表
IP = [58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7]
# 轮函数扩展置换使用的置换表E
roundfun_E = [32,1,2,3,4,5,4,5,6,7,8,9,8,9,10,11,12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,22,23,24,25,24,25,26,27,28,29,28,29,30,31,32,1]
# 轮函数S盒
roundfun_Sbox = [[[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7],[0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8],[4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0],[15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13]],
[[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10],[3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5],[0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15],[13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9]],
[[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8],[13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1],[13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7],[1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12]],
[[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15],[13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9],[10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4],[3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14]],
[[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9],[14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6],[4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14],[11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3]],
[[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11],[10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8],[9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6],[4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13]],
[[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1],[13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6],[1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2],[6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12]],
[[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7],[1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2],[7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8],[2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]
]
# 轮函数中的置换表P
roundfun_P = [16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25]
# 密钥置换选择PC-1和PC-2的值
PC_1 = [57,49,41,33,25,17,9,1,58,50,42,34,26,18,10,2,59,51,43,35,27,19,11,3,60,52,44,36,63,55,47,39,31,23,15,7,62,54,46,38,30,22,14,6,61,53,45,37,29,21,13,5,28,20,12,4]
PC_2 = [14,17,11,24,1,5,3,28,15,6,21,10,23,19,12,4,26,8,16,7,27,20,13,2,41,52,31,37,47,55,30,40,51,45,33,48,44,49,39,56,34,53,46,42,50,36,29,32]
# 各轮密钥循环左移的位数
key_rol_number = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]
# 输入:明文plaintext和密钥key
# 输出:密文ciphertext
# 函数功能:进行DES加密
def DES_encrypt(plaintext, key):
(Li_1, Ri_1) = DES_initial_permutation(IP, plaintext) # 1. 初始置换
(Ci_1, Di_1) = DES_permutation_choice_key1(PC_1, key)
for i in range(16): # 2. 16轮加密
(Li, Ri, Ci, Di) = DES_encrypt_round(i, Li_1, Ri_1, Ci_1, Di_1, roundfun_E, roundfun_Sbox, roundfun_P, key_rol_number, PC_2)
(Li_1, Ri_1, Ci_1, Di_1) = (Li, Ri, Ci, Di)
(L,R) = DES_exchange_32bits(Li, Ri) # 3. 32位互换
ciphertext = DES_invertible_initial_permutation(IP, (L<<32)+R) # 4. 逆初始置换
return ciphertext
print(hex(DES_encrypt(plaintext, key)))