本系列为《模式识别与机器学习》的读书笔记。

一，概率生成式模型

⾸先考虑⼆分类的情形。类别 ${\mathcal{C}}_1$ 的后验概率可以写成

$$\begin{array}{rl}p({\mathcal{C}}_1|\mathbf{x})& =\frac{p(\mathbf{x}|{\mathcal{C}}_1)p({\mathcal{C}}_1)}{p(\mathbf{x}|{\mathcal{C}}_1)p({\mathcal{C}}_1)+p(\mathbf{x}|{\mathcal{C}}_2)p({\mathcal{C}}_2)}\\ & =\frac{1}{1+\exp (-a)}=\sigma (a)\end{array}\text{\hspace{1em}(4.36)}$$
其中，
$$a=\ln \frac{p(\mathbf{x}|{\mathcal{C}}_1)p({\mathcal{C}}_1)}{p(\mathbf{x}|{\mathcal{C}}_2)p({\mathcal{C}}_2)}$$
$\sigma (a)$ 称之为 logistic sigmoid函数 。

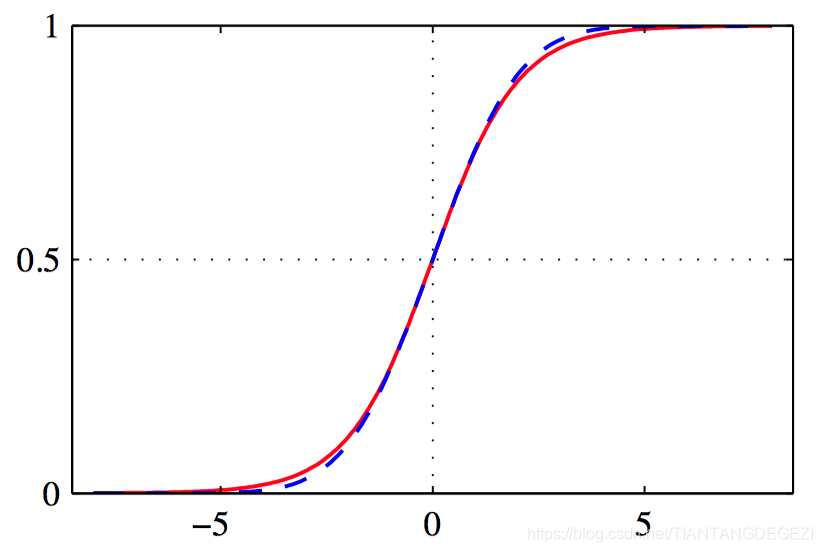
如图4.12，logistic sigmoid函数 $\sigma (a)$ 的图像， ⽤红⾊表⽰，同时给出的是放缩后的逆probit函数 $\Phi (\lambda a)$ 的图像， 其中 ${\lambda }^2=\frac{\pi }{8}$ ， ⽤蓝⾊曲线表⽰。

logistic sigmoid函数 在许多分类算法中都有着重要的作⽤，满⾜下⾯的对称性
$$\sigma (-a)=1-\sigma (a)\text{\hspace{1em}(4.37)}$$
logistic sigmoid的反函数为
$$a=\ln \left(\frac{\sigma }{1-\sigma }\right)\text{\hspace{1em}(4.38)}$$
被称为 logit函数。它表⽰两类的概率⽐值的对数 $\ln [\frac{p({\mathcal{C}}_1|\mathbf{x})}{p({\mathcal{C}}_2|\mathbf{x})}]$ ，也被称为 log odds函数 。

对于 $K>2$ 个类别的情形，有
$$\begin{array}{rl}p({\mathcal{C}}_k|\mathbf{x})& =\frac{p(\mathbf{x}|{\mathcal{C}}_k)p({\mathcal{C}}_k)}{{\sum }_{j}p(\mathbf{x}|{\mathcal{C}}_j)p({\mathcal{C}}_j)}\\ & =\frac{\exp (a_k)}{{\sum }_j\exp (a_j)}\end{array}\text{\hspace{1em}(4.39)}$$
被称为归⼀化指数（normalized exponential），也叫 softmax函数 ，可以被当做logistic sigmoid函数对于多类情况的推⼴。其中， $a_k$ 被定义为
$$a_k=\ln p(\mathbf{x}|{\mathcal{C}}_k)p({\mathcal{C}}_k)$$
如果对于所有的 $j\ne k$ 都有 $a_k\gg a_j$ ，那么 $p({\mathcal{C}}_k|\mathbf{x})\simeq 1$ 且 $p({\mathcal{C}}_j|\mathbf{x})\simeq 0$。

1，连续输⼊

假设类条件概率密度是⾼斯分布，然后求解后验概率的形式。假定所有的类别的协⽅差矩阵相同，这样类别 ${\mathcal{C}}_k$ 的类条件概率为

$$p(\mathbf{x}|{\mathcal{C}}_k)=\frac{1}{(2\pi {)}^{\frac{D}{2}}}\frac{1}{|\mathbf{\Sigma }{|}^{\frac{1}{2}}}\exp \left\{-\frac{1}{2}(\mathbf{x}-{\mathbf{\mu }}_k{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mathbf{\mu }}_k)\right\}\text{\hspace{1em}(4.40)}$$

⾸先考虑两类的情形。根据公式(4.36)，有

$$p({\mathcal{C}}_1|\mathbf{x})=\sigma ({\mathbf{w}}^T\mathbf{x}+w_0)\text{\hspace{1em}(4.41)}$$

其中，
$$\begin{gathered} \mathbf{w}={\mathbf{\Sigma }}^{-1}({\mathbf{\mu }}_1-{\mathbf{\mu }}_2) \\ {w}_0=-\frac{1}{2}{\mathbf{\mu }}_1^T{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_1+\frac{1}{2}{\mathbf{\mu }}_2^T{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_2+\ln \underset{p({\mathcal{C}}_2)}{} \end{gathered}$$