目录
Δ前言
- 博文中涉及的题目均来自《王道数据结构考研复习指导》,《竟成408考研复习全书》,以及《408统考历年真题》,其中真题部分包括09~22年的所有选择题真题。
- 这篇博文只收录了408—数据结构的选择题部分,大题部分单独另出博文。
- 注意事项——①点击文章侧边栏目录或者文章开头的目录可以进行跳转。②解析多是一些解题方法和解题思路,很多解析都是up自己写得,实在简单的题目up没有写解析,请读者自己思考。
- 良工不示人以朴,up所有文章都会适时补充完善。大家如果有问题都可以在评论区进行交流或者私信up。感谢阅读!
一、绪论
1.1 数据结构的基本概念 :
1.以下属于逻辑结构的是(C)。
A.顺序表 B.哈希表 C.有序表 D.单链表
Note :
顺序表、哈希表和单链表是三种不同的数据结构,既描述逻辑结构,又描述存储结构和数据运算。而有序表是指关键字有序的线性表,仅描述了元素之间的逻辑关系,它既可以链式存储,又可以顺序存储,故属于逻辑结构。
2.以下与数据的存储结构无关的术语是(D)。
A.循环队列 B.链表 C.哈希表 D.栈
Note :
数据的存储结构有顺序存储、链式存储、索引存储和散列存储。A选项循环队列是用顺序表实现的队列,是一种数据结构。D选项栈是一种抽象数据类型,可采用顺序存储或链式存储,只表示逻辑结构。数据的逻辑结构独立于其存储结构。
1.2 算法和算法评价 :
3.以下算法的时间复杂度为(D)。
void fun(int n) {
int i = 1;
while (i<=n)
i = i*2;
} A.O(n) B.O(n^2) C.O(nlog[2]n) D.O(log[2]n)
Note :
设最内层语句i = i*2; 执行了t次,则根据while判断条件,有i = 2^t = n,两边同取对数得t = log[2]n,即T(n) = O(log[2]n)。
4.有以下算法,其时间复杂度为(C)。
void fun(int n) {
int i = 0;
while (i*i*i <= n)
i++;
} A.O(n) B.O(nlog[2]n) C.O(n^1/3) D.O(n^1/2)
Note :
设最内层语句i++; 执行了t次,则根据while判断条件,有i = t,t^3 = n,所以t = n^1/3,即T(n) = O(n^1/3)。
5.程序段如下:(王道书上这题的代码有误,不能实现冒泡排序,我进行了修正)
for (i = n-1; i > 0; i--)
for (j = 0; j < i; j++)
if (a[j] > a[j+1])
//exchange code 其中n为正整数,则最后一行语句的频度在最坏情况下是(D)。
A.O(n) B.O(nlog[2]n) C.O(n^3) D.O(n^2)
Note :
该程序段实现的是冒泡排序。冒泡排序是一种稳定的排序方法,其平均时间复杂度为O(n^2),最坏情况下的时间复杂度也为O(n^2)。
6.以下算法中加下划线的语句的执行次数为(A)。
int m = 0, i, j;
for (i = 1; i <= n; i++)
for (j = 1; j <= 2*i; j++)
m++; //这条语句加了下划线 A.n(n+1) B.n C.n + 1 D.n^2
Note :
m初始值为0,“m++;”每执行一次,m的值加一。先算内层,内层for循环执行次数为Σ[1,2i] 1 = 2i;外层for循环继续对2i求和,所以总的执行次数为Σ[1,n] 2i = 2Σ[1,n] i = n(n + 1)。
7.[2011真题] 设n是描述问题规模的非负整数,下面的程序片段的时间复杂度是(A)。
x = 2;
while (x < n/2)
x = 2*x; A.O(log[2]n) B.O(n) C.O(nlog[2]n) D.O(n^2)
Note :
设while循环内层语句x = 2*x;执行了t次,则x = 2^(t + 1),根据while判断条件,有2^(t + 1) = n/2,∴t = log[2](n/2) - 1 = log[2]n - 1,∴T(n) = O(log[2]n)。
8.[2012真题] 求整数n(n ≥ 0) 的阶乘的算法如下,其时间复杂度是(B)。
int fact(int n) {
if (n <= 1) return 1;
return n*fact(n-1);
} A.O(log[2]n) B.O(n) C.O(nlog[2]n) D.O(n^2)
Note :
这是一个简单的递归函数,整个程序的基础操作只有递归处的乘法运算,n次嵌套递归会进行n次压栈,每次递归都执行一次乘法,所以共执行n次乘法。∴T(n) = O(n)。
9.[2013真题] 已知两个长度分别为m和n的升序链表,若将它们合并为长度为 m + n 的一个降序链表,则最坏情况下的时间复杂度是(D)。
A.O(n) B.O(mn) C.O(min{m,n}) D.O(max{m,n})
Note :
类似于“归并排序”的思想,每次从两个升序链表中取出两个元素进行比较(已经选出去的元素不会再进行比较),∵要建立一个降序链表,∴每次将两个元素之中更小的那个元素利用头插法插入到新的降序链表中;若其中一个链表已经没有元素可以比较(全比完了),则直接将另一个链表剩余的元素依次头插到新链表中即可。在最坏情况下,比如两个链表的元素大小交替出现时(eg : A链表——1,3,5;B链表——2,4,6),比较的次数会达到m + n - 1次。而由题设条件可知有不等式2max(m,n) > m+n-1,因此T(n) = O(max{m,n})。
10.[2014真题] 下列程序段的时间复杂度是(C)。
count = 0;
for (k = 1; k <= n; k *= 2)
for (j = 1; j <= n; j++)
count++; A.O(log[2]n) B.O(n) C.O(nlog[2]n) D.(n^2)
Note :
此题比较特殊,外层for循环和内层for循环没有关系(循环变量没有关联),所以可以分别单独计算内外层的时间复杂度,相乘即是最终结果。先算内层,设count++;执行了t次,由内层for的循环判断条件语句可知,t = n;再算外层,同样,由外层for循环的判断条件语句可知,t = log[2]n,所以总的时间复杂度为O(nlog[2]n)。
11.[2017真题] 下列函数的时间复杂度是(B)。
int func(int n) {
int i = 0, sum = 0;
while (sum < n) sum += ++i;
return i;
} A.O(log[2]n) B.O(n^1/2) C.O(n) D.(nlog[2]n)
Note :
设while循环内层语句sum += ++i; 执行了t次,可知sum = 0 + 1 + 2 + 3 + 4 + ... + i(i = t),根据while判断条件,有i*(i+1) / 2 = n,所以T(n) = n^1/2。
12.[2019真题] 设n是描述问题规模的非负整数,下列程序段的时间复杂度是(B)。
x = 0;
while (n >= (x+1) * (x+1))
x = x + 1; A.O(log[2]n) B.O(n^1/2) C.O(n) D.O(n^2)
Note :
设while循环内层语句x = x + 1; 执行了t次,则x = t,根据while判断条件,有(t + 1)^2 = n,∴T(n) = O(n^1/2)。
二、线性表
2.2 线性表的顺序表示 :
13.线性表的顺序存储结构是一种(A)。
A.随机存取的存储结构 B.顺序存取的存储结构
C.索引存取的存储结构 D.散列存取的存储结构
Note :
此题“存取方式”指的是读写方式。顺序表是一种支持随机存取的存储结构,只要根据起始地址加上元素的序号,可以访问到顺序表中任意一个元素。
14.一个线性表最常用的操作是存取任一指定序号的元素并在最后进行插入、删除操作,则利用(A)存储方式可以节省时间。
A.顺序表 B.双链表 C.带头结点的双循环链表 D.单循环链表
Note :
此题ABCD中,只有顺序表可以按元素序号进行随机存取,而不需要进行链表的遍历,且在顺序表最后进行增删操作时,不需要移动任何元素,因此时间开销小。
15.在一个长度为n的顺序表中删除第i (1 ≤ i ≤ n) 个元素时,需向前移动(C)个元素。
A.n B.i - 1 C.n-i D.n-i+1
Note :
注意题干中说的是“删除”操作,所以要移动n-i个元素。Δ注意:线性表中元素的位序是从1开始的,而数组中元素的下标是从0开始的。
16.设线性表有n个元素,严格来说,以下操作中,(C)在顺序表上实现要比在链表上实现的效率高。
Ⅰ.输出第i (1 ≤ i ≤ n) 个元素值
Ⅱ.交换第3个元素和第4个元素的值
Ⅲ.顺序输出这n个元素的值
A.Ⅰ B.Ⅰ、Ⅲ C.Ⅰ、Ⅱ D.Ⅱ、Ⅲ
Note :
对于Ⅰ和Ⅱ,由于顺序表具有“随机存取”的特性,因此在顺序表上实现“改查”效率更高。对于Ⅲ,要求遍历整个线性表,因此顺序表上和链表上时间复杂度相同。
2.3 线性表的链式表示 :
17.下列关于线性表的说法中,正确的是(D)。
Ⅰ.顺序存储方式只能用于存储线性结构
Ⅱ.取线性表的第i个元素的时间与i的大小有关
Ⅲ.静态链表需要分配较大的连续空间,插入和删除不需要移动元素
Ⅳ.在一个长度为n的有序单链表中插入一个新结点并仍保持有序的时间复杂度为O(n)
Ⅴ.若用单链表来表示队列,则应该选用带尾指针的循环链表
A.Ⅰ、Ⅱ B.Ⅰ、Ⅲ、Ⅳ、Ⅴ C.Ⅳ、Ⅴ D.Ⅲ、Ⅳ、Ⅴ
Note :
对于Ⅰ,顺序存储方式同样可以存储树和图(比如一棵只有树干的树);对于Ⅱ,取出线性表中的第i个元素所需要的时间应该考虑线性表的存储方式,以及所取的元素在表中的位置;如果是顺序存储,由于顺序表满足“随机存取”的特性,因此不管i多大,取出一个元素的时间复杂度都是O(1);而如果是链式存储,越靠后的元素,取出所需的时间越长(遍历链表)。
18.给定有n个元素的一维数组,建立一个有序单链表的最低时间复杂度是(D)。
A.O(1) B.O(n) C.O(n^2) D.O(nlog[2]n)
Note :
若先建立单链表,然后通过直接插入排序从前往后查找元素的位置并依次插入,直接插入排序算法的时间复杂度为O(n^2);若先对数组进行排序,再建立对应的单链表,对数组进行排序最好的时间复杂度是O(nlog[2]n),而建立单链表的时间复杂度是O(n),根据时间复杂度计算的加法原则【T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max{f(n), g(n)}),即多项相加,只保留最高阶的项且系数置为1】,总的时间复杂度为O(nlog[2]n)。
19.将长度为n的单链表链接在长度为m的单链表后面,其算法的时间复杂度是(C)。
A.O(1) B.O(n) C.O(m) D.O(n+m)
Note :
由于题中没有提到m链表设有尾指针,因此要先遍历m链表,找到该单链表的尾结点,故时间复杂度为O(n)。
20.在一个长度为n的带头结点的单链表h上,设有尾指针r,则执行()操作与链表的表长有关。
A.删除单链表中的第一个元素
B.删除单链表中的最后一个元素
C.在单链表第一个元素前插入一个新元素
D.在单链表最后一个元素后插入一个新元素
Note :
注意,在408统考中,当提到一个链表具有头结点时,这通常隐含了该链表有一个指向头结点的头指针。对于B选项,删除单链表中最后一个元素时,需要修改其前驱的next指针域,以及修改尾指针r的指向。
21.在长度为n的有序单链表中插入一个新结点,并仍然保持有序的时间复杂度是(B)。
A.O(1) B.O(n) C.O(n^2) D.O(log[2]n)
Note :
假设单链表是递增有序,先找到大于x的结点的直接前驱p,在p之后插入该结点。故T(n) = O(n) + O(1) = O(n)。
22.设对n(n>1) 个元素的线性表的运算只有四种:删除第一个元素;删除最后一个元素;在第一个元素之前插入新元素;在最后一个元素之后插入新元素,则最好使用(C)。
A.只有尾结点指针没有头结点指针的循环单链表
B.只有尾结点指针没有头结点指针的非循环双链表
C.只有头结点指针没有尾结点指针的循环双链表
D.既有头结点指针又有尾结点指针的循环单链表。
Note :
重点关注“删除最后一个元素”的操作,对于A和D,如果要删除最后一个元素,必须修改其直接前驱的指针域和尾结点指针,因此需要遍历整个链表,时间复杂度为O(n)。对于B,删除第一个元素时,需要通过结点的prior指针依次往前找到链表的头结点,时间复杂度为O(n)。对于C,四种操作的时间复杂度均为O(1)。
23.某线性表用带头结点的循环单链表存储,头指针为head,当head->next->next==head成立时,线性表长度可能是(D)。
A.0 B.1 C.2 D.可能为0或1
Note :
注意循环单链表为空时,head->next......->next==head恒成立,因为头结点的指针域始终指向了自己。
24.[2016真题] 已知一个带有表头结点的双向循环链表L,结点结构为[prev, data, next],其中prev和next分别是指向其直接前驱和直接后继结点的指针。现要删除指针p所指的结点,正确的语句序列是(D)。
A.p->next->prev = p->prev; p->prev->next = p->prev; free(p);
B.p->next->prev = p->next; p->prev->next = p->next; free(p);
C.p->next->prev = p->next; p->prev->next = p->prev; free(p);
D.p->next->prev = p->prev; p->prev->next = p->next; free(p);
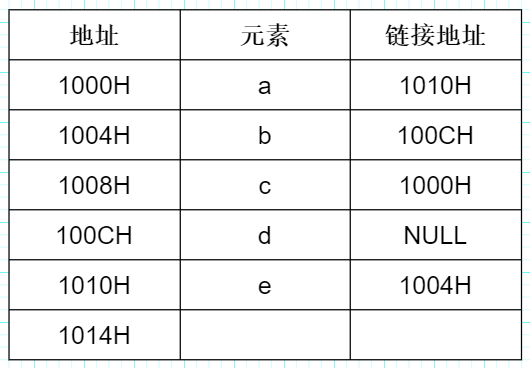
25.[2016真题] 已知表头元素为c的单链表在内存中的存储状态如下表所示 :
现将f 存放于1014H处并插入单链表,若f在逻辑上位于a和e之间,则a,e,f的“链接地址”依次是(D)。
A.1010H, 1014H, 1004H B.1010H, 1004H, 1014H
C.1014H, 1010H, 1004H D.1014H, 1004H, 1010H
26.[2021真题] 已知头指针h指向一个带头结点的非空单循环链表,结点结构为[data,next],其中next是指向直接后继结点的指针,p是尾指针,q是临时指针,现要删除该链表的第一个元素,正确的语句序列是(D)。
A.h->next = h->next->next; q = h->next; free(q);
B.q = h->next; h->next = h->next->next; free(q);
C.q = h->next; h->next = q->next; if(p != q) p = h; free(q);
D.q = h->next; h->next = q->next; if(p == q) p = h; free(q);
Note :
当q和p指向相同时,该非空单循环链表只有一个元素(只有首结点),因此在free(q)之前需要修改尾指针的指向,令其指向头结点,这样free(q)之后整个链表为空。
三、栈、队列和数组
3.1 栈
27.若一个栈的输入序列是1,2,3,...,n,输出序列的第一个元素是n,则第i个输出元素是(D)。
A.不确定 B.n - i C.n - i - 1 D.n - i + 1
Note :
根据栈“先进后出”的特性,当输出序列的第一个元素是n时,表明之前的n - 1个元素已经按顺序依次入栈,∴此时得到的输出序列一定是原序列的逆序列,而n, n-1, ..., 3, 2, 1序列中,第i个元素为n - i + 1。
28.一个栈的输入序列为1,2,3,...,n,输出序列的第一个元素是i,则第j个输出元素是(D)。
A.i - j - 1 B.i - j C.j - i + 1 D.不确定
Note :
To be, or not to be, that is the question.
29.若一个栈的输入序列是P1, P2, ..., Pn,输出序列是1, 2, 3, ..., n, 若P3 = 1,则P1的值(C)。
A.可能是2 B.一定是2 C.不可能是2 D.不可能是3
Note :
由题设条件可知,P3是第一个出栈的元素;根据栈“先进后出"的特性,可知当P3出栈时,P1,P2一定还在栈中,所以下一个出栈的元素不可能是P1,而下一个输出的元素是2,所以P1不可能是2。
30.已知一个栈的入栈序列是1,2,3,4,其出栈序列为P1, P2, P3, P4,则P2, P4不可能是(C)。
A.2,4 B.2,1 C.4,3 D.3,4
Note :
对于C选项,当P2 = 4,P3 = 3时,可知P1只能为1或2,不论P1是1还是2,当P2出栈的时候,3一定还在栈中,而出栈序列下一个元素是P3,所以P4不可能为3。
31.[2009真题] 设栈S 和队列Q 的初始状态均为空,元素abcdefg依次进入栈S,若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是bdcfeag,则栈S 的容量至少是(C)。
A.1 B.2 C.3 D.4
32.[2010真题] 若元素a, b, c, d, e, f依次进栈,允许进栈、退栈操作交替进行,但不允许连续3次进行退栈操作,不可能得到的出栈序列是(D)。
A.dcebfa B.cbdaef C.bcaefd D.afedcb
33.[2011真题] 若元素a, b, c, d, e依次进入初始为空的栈中,若元素进栈后可停留、可出栈,直到所有元素都出栈,则在所有可能的出栈序列中,以元素d开头的序列个数是(B)。
A.3 B.4 C.5 D.6
34.[2013真题] 一个栈的入栈序列为1, 2, 3, ..., n,出栈序列是P1, P2, P3, ..., Pn。若P2 = 3,则P3可能取值的个数是(C)。
A.n - 3 B.n - 2 C.n - 1 D.无法确定
Note :
由栈“先进后出”的特性可知,P3可以取到大于3的任何数;进一步分析可知P3亦可取到1和2,所以P3只取不到3,即P3可能取值的个数是n - 1。
35.[2017真题] 下列关于栈的叙述中,错误的是(C)。
Ⅰ.采用非递归方式重写递归程序时必须使用栈
Ⅱ.函数调用时,系统要用栈保存必要的信息
Ⅲ.只要确定了入栈次序,即可确定出栈次序
Ⅳ.栈是一种受限的线性表,允许其在两端进行操作。
A.仅Ⅰ B.仅Ⅰ、Ⅱ、Ⅲ C.仅Ⅰ、Ⅲ、Ⅳ D.仅Ⅱ、Ⅲ、Ⅳ
Note :
对于Ⅰ,计算斐波那契数列迭代实现只需要一个循环即可实现。
36.[2018真题] 若栈S1 中保存整数,栈S2 中保存运算符,函数F()依次执行下述各步操作:
1)从S1 中依次弹出两个操作数a 和 b。
2)从S2 中弹出一个运算符op。
3)执行相应的运算b op a。
4)将运算结果压入S1 中。
假定S1 中的操作数依次是5, 8, 3, 2(2在栈顶),S2 中的运算符依次是*、-、+(+在栈顶)。调用3次F()后,S1栈顶保存的值是(B)。
A.-15 B.15 C.-20 D.20
37.[2020真题] 对空栈S 进行Push 和 Pop操作,入栈序列为a, b, c, d, e,经过Push, Push, Pop, Push, Pop, Push, Push, Pop操作后得到的出栈序列是(D)。
A.b, a, c B.b, a, e C.b, c, a D.b, c, e
3.2 队列
38.若用数组A[0...5] 来实现循环队列,且当前rear和front的值分别为1 和 5,当从队列中删除一个元素,再加入两个元素后,rear 和 front的值分别为(B)。
A.3 和 4 B.3 和 0 C.5 和 0 D.5 和 1
Note :
循环队列,默认front指向队头元素,rear指向队尾元素的下一个元素。可知数组A的最大容量是6,且当前队列中有2个元素A[5]和A[0],其中队头元素是A[5],队尾元素是A[0];删除一个元素后,front指向从5变成0;加入两个元素后,rear指向从1变成3。
39.用链式存储方式的队列进行删除操作时需要(D)。
A.仅修改头指针 B.仅修改尾指针
C.头尾指针都要修改 D.头尾指针可能都要修改
Note :
注意是“删除”操作,若删除的队头元素不是队列中唯一一个元素,则仅需要修改头指针;若删除的元素是队列中唯一一个元素,则头尾指针都需要进行修改,删除后队列为空,即令rear = front。
40.假设循环单链表表示的队列长度为n,队头固定在链表尾,若只设头指针,则进队操作的时间复杂度为(A)。
A.O(n) B.O(1) C.O(n^2) D.O(nlog[2]n)
Note :
队头在链表尾,说明队尾在链表头,而队列的“进队/入队”操作是在队尾进行的,对应于此题即在链表头进行;又因为该循环单链表只设了头指针,所以删除表头结点的操作本身只需要O(1)的时间复杂度,但是删除后要维护链表“循环”的特性,因此需要遍历链表找到链表表尾结点,故总的时间复杂度T(n) = O(1) + O(n) = O(n)。
41.若以1, 2, 3, 4作为双端队列的输入序列,则既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列是(C)。
A.1, 2, 3, 4 B.4, 1, 3, 2 C.4, 2, 3, 1 D.4, 2, 1, 3
Note :
结论记住即可,C选项,输入或者输出受限的双端队列都得不到该输出序列。B选项,输入受限可得输出受限不可得。D选项,输出受限可得输入受限不可得。
42.[2010真题] 某队列允许在其两端进行入队操作,但仅允许在一端进行出队操作,若元素a,b,c,d,e依次入此队列后再进行出队操作,则不可能得到的出队序列是(C)。
A.b,a,c,d,e B.d,b,a,c,e C.d,b,c,a,e D.e,c,b,a,d
Note :
对于“输出”受限的双端队列,求出队序列时,只需要关心能不能通过入队操作“插”成一个想要的输出序列。
43.[2011真题] 已知循环队列存储在一维数组A[0...n-1]中,且队列非空时,front 和 rear分别指向队头元素和队尾元素。若初始时队列为空,且要求第一个进入队列的元素存储在A[0]处,则初始时front 和 rear的值分别是(B)。
A.0, 0 B.0, n - 1 C.n - 1, 0 D.n - 1, n - 1
Note :
注意,此题中rear的指向与默认的循环队列不同,此题中rear直接指向了队尾元素,这意味着在进行“入队”操作时,“送值”和“指针移动”的顺序会发生改变;在默认的循环队列中,rear指向队尾元素的下一个位置,那么在入队时,需要先送值再进行指针移动(即rear指针顺时针移动1位),而在此题中,需要先令rear指针 + 1,再送值。因此,若想第一个进入队列的元素存储再A[0]处,由于是先移动指针再送值,rear在初始队列为空时必须指向A[0]之前的一个位置,而根据循环队列的特性,A[0]再往前就是数组的末尾了,即n - 1。而由于入队操作不修改front指针,所以front指针直接指向0处。
PS : 注意此题中对队列的判空条件为——(Q.rear - 1) == Q.front。
44.[2014真题] 循环队列放在一维数组A[0...M-1] 中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空。下列判断队空和队满的条件中,正确的是(A)。
A.队空:end1 == end2; 队满:end1 == (end2 + 1) mod M
B.队空:end1 == end2; 队满:end2 == (end1 + 1) mod (M - 1)
C.队空:end2 == (end1 + 1) mod M; 队满:end1 == (end2 + 1) mod M
D.队空:end1 == (end2 + 1) mod M; 队满:end2 == (end1 + 1) mod (M - 1)
Note :
由题设条件可知,这是一个标准的默认循环队列,此题中,end1代表front,end2表示rear。显然选A。关于“队满”条件的判定,联系取余运算mod引入的原因,以及顺序存储的队列——数据结构的定义[宏定义MaxSize]。
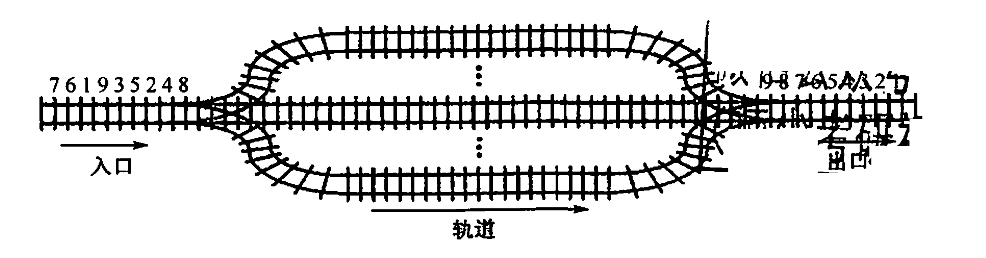
45.[2016真题] 设有如下图所示的火车车轨,入口到出口之间有n条轨道,列车的行进方向均为从左至右,列车可驶入任意一条轨道。现有编号为1~9的9列列车,驶入的次序依次是8, 4, 2, 5, 3, 9, 1, 6, 7。若期望驶出的次序依次为1~9,则n至少是(C)。
A.2 B.3 C.4 D.5
Note :
若要使乱序驶入的火车以“1~9”的顺序依次驶出,需要满足两个条件——①每条轨道上的列车都是降序排列(每条轨道上都是编号小的列车先出来);②编号为1的列车必须位于某条轨道的第一位。可知选C。
46.[2018真题] 现有队列Q 与栈S ,初始时Q中的元素依次是1,2,3,4,5,6(1在队头),S为空。若仅允许下列3种操作:①出队并输出出队元素;②出队并将出队元素入栈;③出栈并输出出栈元素,则不能得到的输出序列是(C)。
A.1,2,5,6,4,3 B.2,3,4,5,6,1 C.3,4,5,6,1,2 D.6,5,4,3,2,1
Note :
根据队列“先进先出”的特性,若没有栈S参与,队列Q的出队序列是唯一的,即1,2,3,4,5,6顺序输出;因此,若想让队列前面的元素之后再输出,就必须让这些元素先进栈,之后再出栈。对于C选项,由于输出序列的第一个元素为3,可知元素1,2此时一定在栈中,根据栈“先进后出”的特性,可知2一定比1先出栈,所以不可能得到C选项中的序列。
47.[2021真题] 初始为空的队列Q的一端仅能进行入队操作,另外一端既能进行入队操作又能进行出队操作。若Q的入队序列是1,2,3,4,5,则不能得到的出队序列是(D)。
A.5,4,3,1,2 B.5,3,1,2,4 C.4,2,1,3,5 D.4,1,3,2,5
3.3 栈和队列的应用
48.利用栈求表达式的值时,设立运算数栈OPEN。假设OPEN只有两个存储单元,则在下列表达式中,不会发生溢出的是(B)。
A.A-B*(C-D) B.(A-B)*C-D C.(A-B*C)-D D.(A-B)*(C-D)
Note :
可以将ABCD分别从中缀转化为后缀,可得A: ABCD-*-,B: AB-C*D-,C: ABC*-D-,D: AB-CD-*,可知ACD都会溢出。
49.[2009真题] 为解决计算机主机与打印机之间速度不匹配的问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入缓冲区,而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是(B)。
A.栈 B.队列 C.树 D.图
50.[2012真题] 已知操作符包括+、-、*、/、(、)。将中缀表达式a+b-a*((c+d)/e-f)+g转换为等价的后缀表达式ab+acd+e/f-*-g+时,用栈来存放暂时还不能确定运算次序的操作符。栈初始为空时,转换过程中同时保存在栈中的操作符的最大个数是(A)。
A.5 B.7 C.8 D.11
Note :
注意,栈中存放的是还不能确定运算次序的操作符,即,当一个运算符已经确定了运算次序时,它就要出栈。中缀表达式从左往后看,第一个+号(a+b)很快就确定了运算次序,因此,第一个+号不会停留在栈中;继续,-, *, (, (, +,一直到扫描到d之前,这五个操作符都没有确定运算次序,因此这五个运算符都还停留在栈中,∴选A。
51.[2014真题] 假设栈初始为空,将中缀表达式a/b+(c*d-e*f)/g转换为等价的后缀表达式的过程中,当扫描到f时,栈中的元素依次是(B)。
A.+(*- B.+(-* C./+(*-* D./+-*
Note :
由于中缀表达式的运算符位于操作数的中间,因此,当扫描到中缀表达式中的运算符时,还无法确定该操作符的运算次序(还不能输出),所以需要一个栈来存放这些还不能确定的操作符。依然是中缀表达式从左往后看,第一个/号很快就确定了运算次序a/b,当扫描到b时第一个/号出栈,不会在栈中停留;继续,+,(,这两个运算符也不能确定次序,依次压栈;继续,c*d次序确定,因此第一个*号不会在栈中停留;继续,-,*,依次压栈。所以,在扫描到f时,栈中的元素依次是+, (, -, *四个运算符。
52.[2015真题] 已知程序如下:
int S(int n)
{ return (n <= 0) ? 0 : S(n-1) + n; }
void main()
{ cout<<S(1); } 程序运行时使用栈来保存调用过程的信息,自栈底到栈顶保存的信息依次对应的是(A)。
A.main() -> S(1) -> S(0) B.S(0) -> S(1) -> main()
C.main() -> S(0) -> S(1) D.S(1) -> S(0) -> main()
3.4 数组和特殊矩阵
53.有一个n*n的对称矩阵A,将其下三角部分按行存放在一维数组B中,而A[0][0]存放于B[0]中,则第i + 1行的对角元素A[i][i]存放于B中的(A)处。
A.(i + 3)i / 2 B.(i + 1)i / 2 C.(2n - i + 1)i / 2 D.(2n - i - 1)i / 2
Note :
由题设条件可知,矩阵下标从[0][0]开始,并且对应存储的数组B下标也是从[0]开始。由于是按行存放,∴到第i行第i列的A[i][i]一共有1 + 2 + ... + i+1个元素(第0行共1个元素,即A[0][0]),即一共有(i + 2)(i + 1) / 2个元素,对应于数组B下标即(i + 2)(i + 1) / 2 - 1,即(i + 3)i / 2。PS : 亦可“特值代入”,取i = 1,A[1][1]对应于B[2]中。
54.在一个二维数组A中,假设每个数组元素的长度为3个存储单元,行下标i为0~8,列下标j为0~9,从首地址SA开始连续存放。在这种情况下,元素A[8][5]的起始地址为(D)。
A.SA + 141 B.SA + 144 C.SA + 222 D.SA + 255
Note :
直接计算当前元素A[8][5]前面有几个元素即可。
55.将三对角矩阵A[1...100][1...100]按行优先存入一维数组B[1...298]中,A中元素A[66][65]在数组B中的位置k为(B)。
A.198 B.195 C.197 D.196
Note :
由题设条件可知,矩阵下标从[1][1]开始,并且对应存储的数组B下标也是从[1]开始。注意三对角矩阵的特点,除了第一行和最后一行只有2个非零元素外,每一行都存放有3个非零元素。具体解题方法同上一题,算就完事儿(A[66][65]前面有194个元素,∴它自己的位置就是194 + 1 = 195)。
56.若将n阶上三角矩阵A按列优先级压缩存放在一维数组B[1...n(n+1)/2+1]中,则存放到B[k]中的非零元素a[i,j](1<=i,j<=n)的下标i, j 与k的对应关系是(C)。
A.i(i+1)/2 + j B.i(i-1)/2 + j - 1 C.j(j-1)/2 + i D.j(j-1)/2 + i - 1
Note :
仍然注意到矩阵A 和 数组B的下标范围。假设B[k]个元素位于矩阵的第j列,由于矩阵采取“列优先”进行存储,所以前面j-1列共j(j-1)/2个元素,而B[k]位于第j列的第i行,由下标关系可知,B[k]是第j列的第i个元素,所以B[k]本身的行列下标和数组下标的关系就是在j(j-1)/2的基础上加上一个i。
57.若将n阶下三角矩阵A按列优先顺序压缩存放在一维数组B[1...n(n+1)/2+1]中,则存放到B[k]中的非零元素a[i,j](1<=i,j<=n)的下标i, j 与k的对应关系是(B)。
A.(j - 1)(2n - j + 1)/2 + i - j B.(j - 1)(2n - j + 2)/2 + i - j + 1
C.(j - 1)(2n - j + 2)/2 + i - j D.(j - 1)(2n - j + 1)/2 + i - j - 1
Note :
回顾——“n, n-1, ..., 3, 2, 1”序列中,第i个元素为n - i + 1。
由于是列优先存储,设B[k]位于矩阵中第j列;仍然先分析前面j - 1列的元素,第1列有n个元素,第j - 1列有n - (j - 1) + 1 = n - j + 2个元素,所以前面 1 到 j-1 列一共的元素是Σ[1, j-1] = (j-1)(2n - j + 2)/2。由于B[k]位于矩阵第j列,而第j列一共有n - j + 1个有效元素,即第j列从上往下有n - (n-j+1) = j - 1个零元素,对于下三角矩阵,位于上三角区的零元素是不会被存储在对应的数组B中的,所以第j列到B[k] 真正存储的有效元素是i - (j-1) = i - j + 1。所以i,j,k最后的对应关系,就是把前j - 1列存储的元素和第j 列存储的元素加起来,即(j-1)(2n - j + 2)/2 + i - j + 1。
58.[2016真题] 有一个100阶的三对角矩阵M,其元素m[i,j](1 <= i,j <=100)按行优先依次压缩存入下标从0开始的一维数组N中。元素m[30,30] 在N中的下标是(B)。
A.86 B.87 C.88 D.89
Note :
认真计算即可,注意计算元素个数时,元素m也包含在内,因为题干问的就是元素m在数组中的下标。同时注意矩阵和数组下标的表示范围。
59.[2017真题] 适用于压缩存储稀疏矩阵的两种存储结构是(A)。
A.三元组表和十字链表 B.三元组表和邻接矩阵
C.十字链表和二叉链表 D.邻接矩阵和十字链表
Note :
十字链表将行单链表和列单链表结合起来存储稀疏矩阵。二叉链表又名左孩子右兄弟表示法,可用于表示树或森林。
60.[2018] 设有一个12*12的对称矩阵M,将其上三角部分的元素m[i,j](1 <= i <= j <= 12)按行优先存入C语言的一维数组N中,元素m[6,6]在N中的下标是(A)。
A.50 B.51 C.55 D.66
Note :
①“上三角部分”包括主对角线元素,区分于“上三角区”的概念。
②C语言一维数组,下标默认从0开始。本题对称矩阵下标从1开始。
③m[6,6] 在本题的对称矩阵中,是第6行第一个元素(对角线元素)。
61.[2020真题] 将一个10*10对称矩阵M的上三角部分的元素m[i,j](1 <= i <= j <= 10)按列优先存入C语言的一维数组N中,元素m[7,2] 在N中的下标是(C)。
A.15 B.16 C.22 D.23
Note :
利用对称矩阵的特性,m[7,2] 实则就是存储m[2,7],从而计算即可(注意是列优先)。
62.[2021真题] 二维数组A 按行优先方式存储,每个元素占用1个存储单元。若元素A[0][0]的存储地址是100,A[3][3]的存储地址是220,则元素A[5][5]的存储地址是(B)。
A.295 B.300 C.301 D.306
Note :
设每行有x个元素,由A[0][0] 和 A[3][3]的存储地址可知,3x + 3 = (220-100),得x = 39;∴A[5][5]的存储地址为100 + (39*5 + 5) = 300。
四、串
4.2 串的模式匹配
63.[2015真题] 已知字符串S为 'abaabaabacacaabaabcc',模式串t为 'abaabc'。采用KMP算法进行匹配,第一次出现“失配”(s[i] ≠ s[j])时,i = j = 5,则下次开始匹配时,i 和 j的值分别是(C)。
A.i=1, j=0 B.i=5, j=0 C.i=5,j=2 D.i=6, j=2
Note :
注意到,S[]下标从0开始。由于采用KMP算法进行匹配,因此主串S的指针i不变,∴i = 5;模式串t的指针回退到相同前缀处进行比较,∴j = 2。
64.[2019真题] 设主串T = 'abaabaabcabaabc',模式串S = 'abaabc',采用KMP算法进行模式匹配,到匹配成功时为止,在匹配过程中进行的单个字符间的比较次数是(B)。
A.9 B.10 C.12 D.15
Note :
当第一次出现“失配”时,比较了6次(第6次时失配),主串指针保持不变,模式串从第三个字符开始比较,因此再比较4次,共10次。
五、树与二叉树
5.1 树的基本概念
回顾——树的性质(设T表示一棵树;n为树的结点总数;h为树的高度;k为树的度数)
①n等于T中所有结点的度数之和加1。
②T的第i层(i≥1)最多有k^(i-1) 个结点。
③T中最多有(k^h - 1) / (k -1)个结点。
④T的最小高度为⌈log[k](n(k - 1) + 1)⌉。(注意向上取整符号)
⑤T的最大高度为n - k + 1。
65.树的路径长度是从树根到每个结点的路径长度的(A)。
A.总和 B.最小值 C.最大值 D.平均值
Note :
“树的路径长度” 概念,要区分于哈夫曼树的带权路径长度。WPL = 树中所有叶结点的带权路径长度(经过的边数 * 该结点权值)之和。
66.对于一棵具有n个结点、度为4的树来说,(A)。
A.树的高度至多是n - 3 B.树的高度至多是n - 4
C.第i层上至多有4(i - 1)个结点 D.至少在某一层上正好有4个结点
Note :
要想让已知结点数的树尽可能地高,就必须让这棵树尽可能地瘦长(即每层结点数尽可能的少),设树高为h,根据题设条件可知h + 3 = n,∴h = n - 3。对于D选项,应该是某个结点正好有四个结点,而不是某一层。
67.[2010真题] 在一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶结点个数是(B)。
A.41 B.82 C.113 D.122
Note :
设树T中共有x个叶结点。利用树的性质①,可知:20*4 + 10*3 + 1*2 + 10*1 + 1 = 20 + 10 + 1 + 10 + x,解得x = 82。
5.2 二叉树的概念
68.设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为(B)。
A.h B.2h - 1 C.2h + 1 D.h + 1
Note :
画图,已知高度h,题干问“结点数至少”,因此二叉树要尽可能地瘦高;可知除了根结点所在的第一层外,每一层都是2个结点,∴总的结点数 = 2(h - 1) + 1 = 2h - 1,所以选B。
69.设二叉树有2n个结点,且m < n,则不可能存在(C)的结点。
A.n个度为0 B.2m个度为0 C.2m个度为1 D.2m个度为2
Note :
①“排除法”,设n = 3,即构造一棵有6个结点的二叉树(画图),由题干条件可知,m = 1或m = 2,排除(A)(B)(D)。
②“直接法”,利用二叉树的性质1可求。
70.设二叉树只有度为0和度为2的结点,其结点个数为15,则该二叉树的最大深度为(C)。
A.4 B.5 C.8 D.9
Note :
解法同68题。设二叉树深度为h,得2h - 1 = 15,∴h = 8。
71.高度为h的完全二叉树最少有(C)个结点。
A.2^h B.2^h + 1 C.2^(h-1) D.2^h - 1
Note :
“排除法”,画一棵完全二叉树,最下面一层只有最左面一个左孩子结点,秒了。
72.一棵有124个叶子结点的完全二叉树,最多有(B)个结点。
A.247 B.248 C.249 D.250
Note :
∵有124个叶子结点,∴二叉树至少有8层(2^7),而124个叶子结点可以分布在最后一层(即第8层) 和 倒数第二层(第7层)。注意,由于是完全二叉树,最后一层每删除两个连续叶子结点,上一层就会暴露出一个叶子结点(注意这个叶子结点本身是完全二叉树本就有的结点),∴为了使完全二叉树整体有最多的结点,并且还要满足124个叶子结点的要求,可知最后一层应该删除7个结点,这样第8层共121个叶子结点,加上上一层暴露出来的3个结点,正好是124个叶子结点,而这么做的话要比删除8个结点多出1个结点——即最后一层的左孩子结点。由于前面7层加起来有127个结点,所以结点总数 = 127 + 121 = 248。
73.已知一棵有2011个结点的树,其叶结点个数是116,该树对应的二叉树中无右孩子的结点个数是(D)。
A.115 B.116 C.1895 D.1896
Note :
“特值法”秒了。由于2011 - 116 = 1895,画图,前面1895层每层一个结点,最后一层有116个叶结点,根据普通树转化为二叉树的原则,只有最后一行的前115个结点有右孩子,其他所有结点均没有右孩子。
74.[2009真题] 已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则该完全二叉树的结点个数最多是(C)。
A39 B.52 C.111 D.119
Note :
注意,第6层有8个叶结点,会有两种情况——①第6层就是最后一层,最后一层共有8个叶结点;②第6层不是最后一层,8个叶结点是最后一层删除连续的叶结点后,上一层所暴露出来的叶结点。
题干问整棵树的结点个数最多,所以考虑第二种情况。1~6层共有2^6 - 1 = 63个结点。而第7层(最后一层)的叶结点个数,是第7层总的叶结点数 - 删除的叶结点数 = 2^6 - 8*2 = 64 - 16 = 48。所以整棵树的结点总数 = 63 + 48 = 111个。
75.[2011真题] 若一棵完全二叉树有768个结点,则该二叉树中叶结点的个数是(C)。
A.257 B.258 C.384 D.385
Note :
768个结点,∴至少有10层(10层全满为2^10 - 1 = 1023个结点)。前面9层一共有2^9 - 1 = 511个结点,所以第10层(最后一层)一共有768 - 511 = 257个结点(叶结点)。又因为257是奇数,所以第9层存在一个只有左孩子的非叶结点。第10层全满有2^9 = 512个结点,∴第9层由于删除而暴露出的叶结点的个数 = (512 - 257 - 1) / 2 = 254 / 2 = 127。∴该二叉树总的叶结点个数 = 257 + 127 = 384。
76.[2018真题] 设一棵非空完全二叉树T的所有叶结点均位于同一层,且每个非叶结点都有2个子结点。若T有k个叶结点,则T的结点总数是(A)。
A.2k - 1 B.2k C.k^2 D.2^k - 1
Note :
由题设条件可知,这是一棵满二叉树,且最后一层有k个结点(叶结点)。由二叉树的性质1可知,k = n2 + 1,得:n2 = k - 1,∴结点总数 = n0 + n2 = k + (k - 1) = 2k - 1。
77.[2020真题] 对于任意一棵高度为5且有10个结点的二叉树,若采用顺序存储结构保存,每个结点占1个存储单元(仅存放结点的数据信息),则存放该二叉树需要的存储单元至少是(A)。
A.31 B.16 C.15 D.10
Note :
尤其注意题干中“任意”这两个字。由于二叉树已经限定是5层,所以存储的结点数的范围是(2^4 - 1) + 1 到 2^5 - 1,即16 到 31,又因为题干问的是“至少”,即满足任意性的所有可能的二叉树,所以是31。(如果问的是最少,则为16)。
5.3 二叉树的遍历和线索二叉树
78.设n,m为一棵二叉树上的两个结点,在中序遍历时,n在m前的条件是(C)。
A.n在m右方 B.n是m祖先 C.n在m左方 D.n是m子孙
Note :
根据中序遍历“左根右”的特点,要想让n在m之前遍历,需要满足以下三种情况之一:①n在m的左子树上;②n是m的左兄弟;③m在n的右子树上。可知,以上三种情况均满足“n在m左方”。
79.设n,m为一棵二叉树上的两个结点,在后序遍历时,n在m前的条件是(D)。
A.n在m右方 B.n是m祖先 C.n在m左方 D.n是m子孙
Note :
后序遍历的特点是“左右根”,因此只要满足n是m子孙,n一定会在m之前遍历。
80.先序为A,B,C,后序为C,B,A的二叉树共有(D)。
A.1棵 B.2棵 C.3棵 D.4棵
Note :
后序特性“左右根”,因此BC在A的左右子树的情况都要考虑到(可直接画出)。
81.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足(C)。
A.所有的结点均无左孩子 B.所有的结点均无右孩子
C.只有一个叶结点 D.是任意一棵二叉树
Note :
根据80题的图形,排除法秒了。(先序ABC,后序CBA)
82.线索二叉树是一种(C)结构。
A.逻辑 B.逻辑和存储 C.物理 D.线性
Note :
物理结构 == 存储结构
83.若X是二叉中序线索树中一个有左孩子的结点,且X不为根,则X的前驱为(C)。
A.X的双亲 B.X的右子树中最左的结点
C.X的左子树中最右的结点 D.X的左子树中最右的叶结点
Note :
中序遍历,又因为X有左孩子,所以X的前驱一定为其左子树的遍历序列中最后的一个结点。其左子树的遍历仍然满足“左根右”的特性,注意,X的左子树中最右的结点可能是一个右孩子(最右的叶结点),也可能是一个只有左孩子的分支结点。
84.(C)的遍历仍需要栈的支持。
A.前序线索树 B.中序线索树 C.后序线索树 D.所有线索树
Note :
后序遍历“左右根”,最后访问根结点,但由于根结点的右孩子不一定为空(,所以需要一个栈来保存相关信息。
85.[2009真题] 给定二叉树如下图所示。设N代表二叉树的根,L代表根结点的左子树,R代表根结点的右子树。若遍历后的结点序列是3175624,则其遍历方式是(D)。
A.LRN B.NRL C.RLN D.RNL
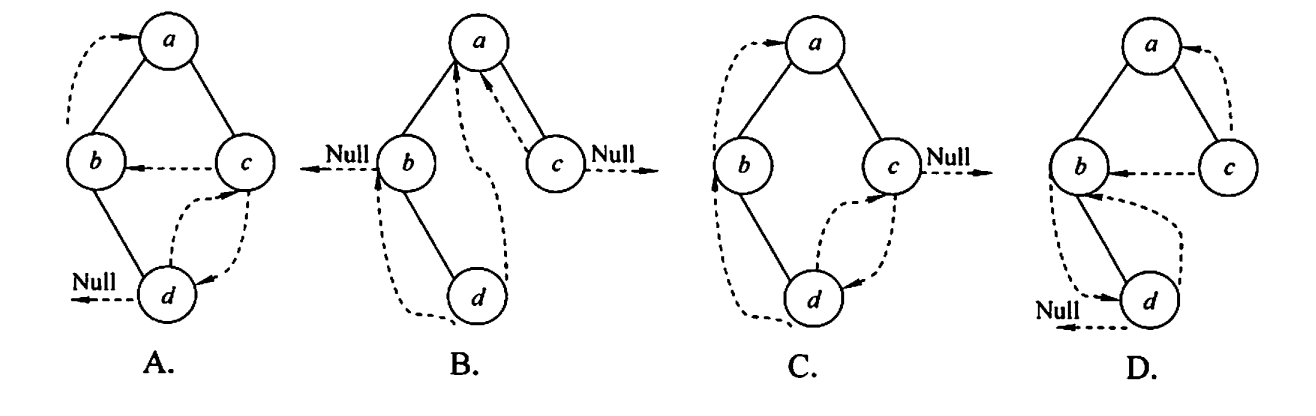
86.[2010真题] 下列线索二叉树中(用虚线表示线索),符后后序线索树定义的是(D)。
87.[2011真题] 一棵二叉树的前序遍历序列和后序遍历序列分别是1,2,3,4 和 4,3,2,1,该二叉树的中序遍历序列不会是(C)。
A.1,2,3,4 B.2,3,4,1 C.3,2,4,1 D.4,3,2,1
88.[2012真题] 若一棵二叉树的前序遍历序列为a,e,b,d,c,后序遍历序列为b,c,d,e,a,则根结点的孩子结点(A)。
A.只有e B.有e,b C.有e,c D.无法确定
Note :
由先序“根左右”,后序“左右根”的特性可知,a为根结点,e一定为a的左孩子或右孩子,假设e为a的左孩子,则只需要判断a是否有右孩子,又因为后序遍历序列中e后面紧接着遍历a,可知a的孩子结点只有e。
89.[2013真题] 若X是后序线索二叉树中的叶结点,且X存在左兄弟结点Y,则X的右线索指向的是(A)。
A.X的父结点 B.以Y为根的子树的最左下结点
C.X的左兄弟结点Y D.以Y为根的子树的最右下结点
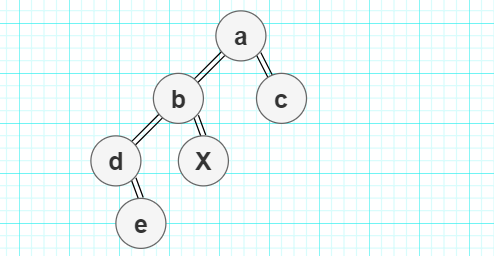
90.[2014真题] 若对下图所示的二叉树进行中序线索化,则结点X的左、右线索指向的结点分别是(D)。
A.e,c B.e,a C.d,c D.b,a
91.[2015真题] 先序序列为a,b,c,d 的不同二叉树的个数是(B)。
A.13 B.14 C.15 D.16
Note :
①技巧——先序序列和中序序列的关系:相当于以先序序列为入栈次序,以中序序列为出栈次序。根据卡特兰数(1/n+1)*C[2n,n],将n = 4代入可得14。
②亦可直接手动写出所有可能结果:先假设b,c,d均在A的左子树上,有5种可能,根据对称关系,可知b,c,d都在A的左子树或右子树上的情况共有10种可能。再写出b,c,d不在同一棵子树下的情况,共4种可能(注意,当A既有左孩子又有右孩子时,不存在对称情况,因为要满足先序遍历“根左右”的特性,左右子树不能随便交换)。
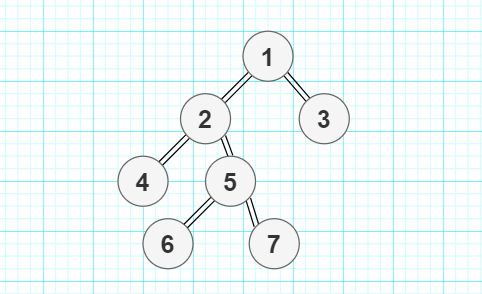
92.[2017真题] 某二叉树的树形如下图所示,其后序序列为e,a,c,b,d,g,f,树中与结点a同层的结点是(B)。
A.c B.d C.f D.g
93.[2017真题] 要使一棵非空二叉树的先序序列与中序序列相同,其所有非叶结点须满足的条件是(B)。
A.只有左子树 B.只有右子树
C.结点的度均为1 D.结点的度均为2
Note :
先序“根左右”,中序“左根右”,当树中所有分支结点都没有左孩子时,可知两序列相同。此题亦可通过画图的方式用排除法。对于C选项,并不是充分条件。
5.4 树、森林
94.利用二叉链表存储森林时,根结点的右指针是(D)。
A.指向最左兄弟 B.指向最右兄弟 C.一定为空 D.不一定为空
Note :
AB选项表述不清楚。但D选项一定对。森林转换为二叉树,当森林中只有一棵树时,根结点的右指针域为空;当森林中出现第二棵树时,根结点的右指针将指向原先第二棵树的根结点。
95.设F是一个森林,B是由F变换来的二叉树。若F中有n个非终端结点,则B中右指针域为空的结点有(C)个。
A.n - 1 B.n C.n + 1 D.n + 2
Note :
对于F中的非终端结点,其所有孩子结点在转换之后,最后一个孩子结点的右指针域一定为空,所以森林中的n个非终端结点对应到二叉树中会出现n个右指针域为空的结点。又因为森林中最后一棵树的根结点,转换到二叉树中是二叉树根结点的最右孩子结点,其右指针域也为空。所以总的右指针域为空的结点有n + 1个。
结论——树转换为二叉树时,对应二叉树中无右孩子的结点个数 = 分支结点数 + 1。
96.[2009真题] 将森林转换为对应的二叉树,若在二叉树中,结点u 是结点v 的父结点的父结点,则在原来的森林中,u 和 v可能具有的关系是(B)。
Ⅰ.父子关系 Ⅱ.兄弟关系 Ⅲ.u 的父结点与v 的父结点是兄弟关系。
A.只有Ⅱ B.Ⅰ和Ⅱ C.Ⅰ和Ⅲ D.Ⅰ、Ⅱ和Ⅲ
Note :
尝试画出二叉树中可能出现的情况:对于Ⅰ,u的左孩子的右孩子是v;对于Ⅱ,u的右孩子的右孩子是v;对于Ⅲ,直接证明不太好证,想到“反证法”,假设Ⅲ成立,则无法得到“结点u 是结点v 的父结点的父结点”的题目条件,所以假设不成立,Ⅲ不成立。
97.[2011真题] 已知一棵有2011个结点的树,其叶结点个数是116,该树对应的二叉树中无右孩子的结点个数是(D)。
A.115 B.116 C.1895 D.1896
Note :
见本篇博文5.2 二叉树的概念——73题原题。
98.[2014真题] 将森林F转换为对应的二叉树T,F中叶结点的个数等于(C)。
A.T中叶结点的个数 B.T中度为1的结点个数
C.T中左孩子指针为空的结点个数 D.T中右孩子指针为空的结点个数
Note :
森林中的叶结点,若其有右兄弟,则转为二叉树后其右指针不为空;但转为二叉树后其左指针一定为空。
99.[2016真题] 若森林F有15条边、25个结点,则F包含树的个数是(C)。
A.8 B.9 C.10 D.11
Note :
结论——由于一棵树中,除根结点外,每个结点都有唯一确定的双亲(父结点),所以,除根结点外每个结点唯一对应有一条边;∴在n个结点的树中有n - 1条边,即每棵树的结点数比边数多1。对应于此题,25 - 15 = 10,结点数共比边数多10,所以森林中有10棵树。
100.[2019真题] 若将一棵树T转化为对应的二叉树BT,则下列对BT的遍历中,其遍历序列与T的后根遍历序列相同的是(B)。
A.先序遍历 B.中序遍历 C.后序遍历 D.按层遍历
101.[2020真题] 已知森林F及与之对应的二叉树T,若F的先根遍历序列是a,b,c,d,e,f,中根遍历序列是b,a,d,f,e,c,则T的后根遍历序列是(C)。
A.b,a,d,f,e,c B.b,d,f,e,c,a C.b,f,e,d,c,a D.f,e,d,c,b,a
Note :
实质是求二叉树的先序中序和后序遍历序列的问题。
102.[2021真题] 某森林F对应的二叉树为T,若T的先序遍历序列是a,b,d,c,e,g,f,中序遍历序列是b,d,a,e,g,c,f,则F中树的棵树是(C)。
A.1 B.2 C.3 D.4
5.5 树与二叉树的应用
103.设哈夫曼编码的长度不超过4,若已对两个字符编码为1 和 01,则还最多可对(C)个字符编码。
A.2 B.3 C.4 D.5
Note :
哈夫曼编码属于前缀编码,而前缀编码的特点是“没有一个编码是另一个编码的前缀”,由此特性可知,若想进行最多的编码,应该从长度更长的编码开始考虑,因此得到0000,0001,0010,0011四个。
104.一棵哈夫曼树共有215个结点,对其进行哈夫曼编码,共能得到(B)个不同的码字。
A.107 B.108 C.214 D.215
Note :
在哈夫曼编码(Huffman Coding)中,“不同的码字”(unique code words)指的是代表不同字符或符号的、互不相同的编码。
105.若度为m的哈夫曼树中,叶子结点个数为n,则非叶子结点的个数为(C)。
A.n - 1 B.⌊n/m⌋ - 1 C.⌈(n - 1)/(m - 1)⌉ D.⌈n/(m - 1)⌉ - 1
Note :
回顾——在n个结点的树中有n - 1条边,即每棵树的边的个数总是等于结点数减去1。
由一般哈夫曼树(二叉树)的定义可知,度为m的哈夫曼树中只有度为0和度为m的结点,设度为m的结点(即非叶子结点)的个数为x,每个度为m的结点都贡献了m条边;根据树的性质,边的个数也等于总结点数 - 1,因此可列出等式:mx = n + x - 1,移项化简可得:x = ⌈(n - 1)/(m - 1)⌉。
106.下列关于并查集的叙述中,(D)是错误的。
A.并查集是用双亲表示法存储的树
B.并查集可用于实现克鲁斯卡尔算法
C.并查集可用于判断无向图的连通性
D.在长度为n的并查集中进行查找操作的时间复杂度为O(log[2]n)
Note :
未做路径优化的并查集在最坏情况下的时间复杂度为O(n)。
107.[2010真题] n(n≥2)个权值均不相同的字符构成哈夫曼树,关于该树的叙述中,错误的是(A)。
A.该树一定是一棵完全二叉树
B.树中一定没有度为1的结点
C.树中两个权值最小的结点一定是兄弟结点
D.树中任一非叶结点的权值一定不小于下一层任一结点的权值
108.[2014真题] 5个字符有如下4种编码方案,不是前缀编码的是(D)。
A.01, 0000, 0001, 001, 1 B.011, 000, 001, 010, 1
C.000, 001, 010, 011, 100 D.0, 100, 110, 1110, 1100
109.[2015真题] 下列选项中给出的是从根分别到达两个叶结点路径上的权值序列,属于同一棵哈夫曼树的是(D)。
A.24,10,5 和 24,10,7 B.24,10,5 和 24,12,7
C.24,10,10 和 24,14,11 D.24,10,5 和 24,14,6
Note :
注意,24 = 10 + 14。24 ≠ 10 + 12。
110.[2017真题] 已知字符集{a,b,c,d,e,f,g,h},若各字符的哈夫曼编码依次是0100,10,0000,0101,001,011,11,0001,则编码序列0100011001001011110101的译码结果是(D)。
A.a c g a b f h B.a d b a g b b C.a f b e a g d D.a f e e f g d
Note :
根据首尾译码,可排除AB,又因为中间连续两个“001”,即连续两个e,所以选D。
111.[2018真题] 已知字符集{a,b,c,d,e,f},若各字符出现的次数分别为6,3,8,2,10,4,则对应字符集中各字符的哈夫曼编码可能是(A)。
A.00, 1011, 01, 1010, 11, 100 B.00, 100, 110, 000, 0010, 01
C.10, 1011, 11, 0011, 00, 010 D.0011, 10, 11, 0010, 01, 000
Note :
由前缀编码的特点,首先排除BC,构造哈夫曼树可知,根结点到6的路径为2,所以排除D。
112.[2019真题] 对n个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有115个结点,则n的值是(C)。
A.56 B.57 C.58 D.60
113.[2021真题] 若某二叉树有5个叶结点,其权值分别为10,12,16,21,30,则其最小的带权路径长度(WPL)是(B)。
A.89 B.200 C.208 D.289
Note :
回顾——树的WPL的定义:树中所有叶结点的带权路径长度之和称为该树的带权路径长度。
六、图 || 七、查找 || 八、排序
每次写博文写到2万字左右,CSDN的编辑器就开始一卡一卡的,可能是我的网络有点拉。没办法,第六章“图”的习题带有大量图片,如果继续在这篇博文里面写,“图、查找、排序”都完成预计一共有4万字左右,估计要卡爆了。人不能让尿憋死,还是老方法,剩余的“图、查找、排序”的内容单独另开一篇博文作为补充,可不是因为我能再氵一篇博文(。
补充的博文写完后,我会把链接挂在下面。链接如下:
System.out.println("END------------------------------------");