前言——
很抱歉以这样的方式讲DP。但是现在的时间必须开始高级的算法了。
实际上到现在,我还没有完全弄明白基础DP怎么做好,但是没办法,等等吧。
今天的状态压缩动态规划就是我们常说的“状压DP”,它的思想很简单,但是操作很难。所以今天恐怕最难的部分反而是“前置知识”
正文——
1、前置知识:集合和二进制
集合是由一定元素构成的一个整体,我们这里说几种集合状态。
1.1 交集
交集简单来说就是两个集合重复的部分。严谨一点的数学表达是
交集是由属于A且属于B的相同元素组成的集合,数学符号是"∩"。
如果画成文氏图,那么就是这样
交集所对应的位运算就是与运算,数学上是AND,程序上的符号是’&',在二进制里就是同为1的时候取1,否则取0的操作。
比如,两个二进制串:
111010
100100
那么进行与运算后的结果就是
100000
补充1 集合运算和二进制运算的理解
实际上仔细想一想,会发现二进制和集合的理解上是有一定冲突的。一个集合需要元素的存在,但是如果二进制串的0/1只是表示为“元素是否存在”,那么这种方式并不具体。
简单点说,你可以说这是一个元素,这个元素是有确切指明的。但是如果你说这个元素存在,那么这个元素到底是什么呢?这样的理解就模糊了。
举个例子,二进制的与运算是相同位置为1取1,但是如果一个位置仅仅是表达存在不存在,那么两个二进制串标1的位置完全可以对应同一个元素啊,那样不就全乱了套了吗?
所以对于二进制串表示的集合,更确切的理解方式是:
对于一个二进制串,它的第i位表示对应特定集合中的第i个元素存在
你可能不明白这种表示方式和感性理解的区别,但是别急,当你看到状压的方式时你会明白一切。这是似乎是一种唯一且最有效的表达方式。
现在来看,这就能解释为什么二进制的与运算是“同位为1取1”,因为两个串第同一位置才对应相同的元素。
1.2 并集
听上去这个名字不好理解,但是实际上就是只要存在于两个集合的元素组成的集合。
准确的数学表达是:
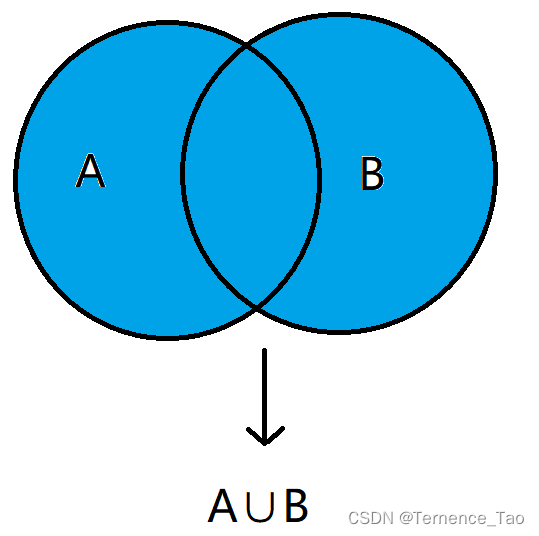
并集由所有属于A或属于B的元素所组成的集合,数学符号是“∪”。
如果画成文氏图,就是这样:
不难看出并集对应的集合运算就是二进制中的或运算,数学上称作OR,注意这里的对应的程序中的运算符是’|‘,而不是’||'。前者是位运算符,后者是逻辑运算符。
在二进制里的运算就是对应位只要有1就得1,全是0才得0,换句话说就是对应位置的相同元素只要存在于一个集合就可以了。
一个简单的例子:
111010
100100
结果为:
111110
1.3 补集和差集
已经讲了或运算,与运算,还剩下什么二进制运算?
是的,补集对应的集合操作是异或运算,程序里的运算符是’^'。
我们还是先看补集的定义,这个定义实际上是有点麻烦的。
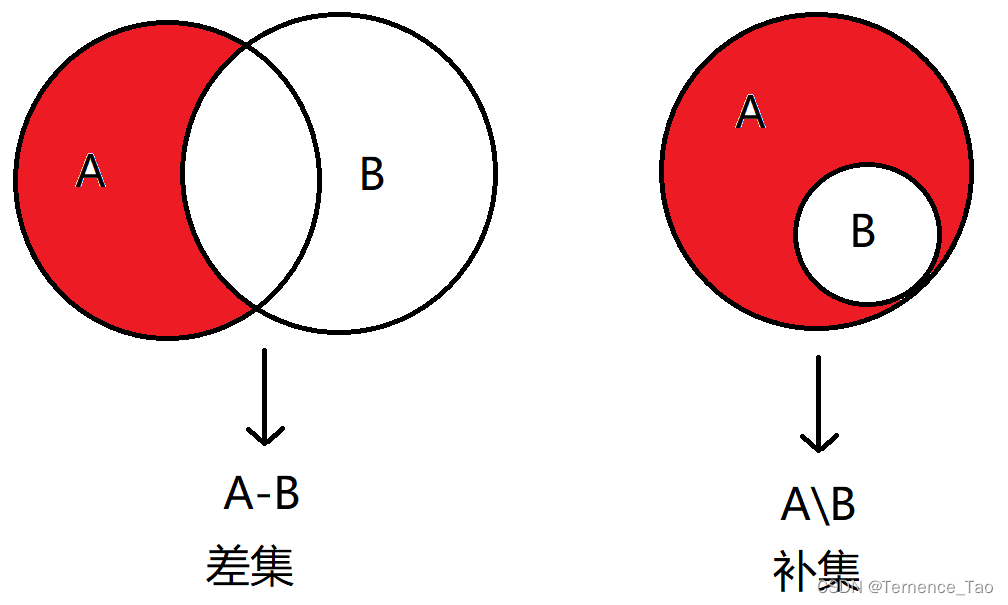
由属于A而不属于B的元素组成的集合,称为B关于A的差集,当A是全集时,称为B关于A的补集。数学上记作A-B或A\B,即A-B={x|x∈A,且x∉B}。
我们还是看张文氏图:
这里注意,一般来说补集对应的是全集和子集的关系(子集在后面讲),而差集和补集的定义基本类似,但是差集是两个集合的相对关系。
对应到二进制里,同一位对应元素中只能存在于1个集合,所以就是不同取1,相同取0的异或运算,但是注意,异或只针对补集,就是确定两者有子集关系的情况下,否则更稳妥的方式是A&(~B)。(不同时存在于两个集合的元素)。
我们还是给个例子
111010
100100
异或后:
011110
附表1 集合和二进制运算
| 集合类型 | 集合符号 | 二进制运算 | 二进制符号 |
|---|---|---|---|
| 交集 | ∩ | 与运算 | & |
| 并集 | ∪ | 或运算 | | |
| 补集 | - \ | 异或运算 | ^ |
1.4 子集
我们先看定义:
设S,T是两个集合,如果S的所有元素都属于T ,即x∈S ⇒x∈T,则称S是T的子集,记为 S⊆T
这个数学符号’∈’ 记得记一下,它表示“子集”。定义如上所示,一个集合中的元素都存在另一个集合。而’⫋’表示真子集,就是说这个子集S并不包含T的所有元素(人话说就是S!=T)。
子集上的有关操作我们放到后面说,牵扯到集合运算
1.5 二进制操作
这个部分按道理说应该和前面的集合部分分开讲,但是都是前置知识。所以就放一起了。
我们刚刚说的是二进制的运算,这里是二进制的特有操作:左移,右移,非。
左移(<<)
左移就是将整个二进制串向左移动,出现空位补0,溢出丢弃。
二进制串10101011,向左移动2位,那么表示方法是10101011<<2。结果易得是1010101100,如果这个二进制只存储8位,那么这个结果就变成10101100。左移可以直接理解为*2
右移(>>)
这个和左移思路是完全一样的,向右移动,高位补0,溢出的时候舍弃的是低位。比如一个二进制串10101011,右移4位,就是000010101011,如果只存8位,那么就是00001010。
和左移类似,右移理解为/2。
非(~)
这里还是请各位注意,这个非不是逻辑运算符,而是位运算符。
非的理解还是1变0,0变1,不过这里是对一个二进制数按位进行取反。最终得到一个新数。
二进制串10101011,按位取反之后就是01010100,不存在溢出情况。
附表2 二进制的特有操作
| 操作符 | 运算含义 | 溢出处理 |
|---|---|---|
| << | 左移,将整个二进制数向左移动 | 丢弃高位 |
| >> | 右移,将整个二进制数向右移动 | 丢弃低位 |
| ~ | 非,按位取反 | 无 |
1.6 二进制和集合运算结合操作
这里的操作都很常见,我决定直接整理一张表。
| 操作 | 意义 |
|---|---|
| 1<<(i-1) | 将第i个元素映射到状态里(从1开始计数) |
| (A&B)==A /(A|B)==B | 判断A是否是B的子集 |
| B&(1<<(i-1))>0 | 判断第i个元素是否属于集合B |
| (s&(1<<(i-1))) | 判断s的第i位是否为1 |
| (s|(1<<(i-1))) | 将s的第i位改为1 |
| s&(s-1) | 将s的最后一个1去除 |
| s&(~(1<<i) | 将s的第i位改为0 |
还有一些求补集,全集这些的操作,我都不列举了。这些只要有集合运算的知识自己很轻松可以推出来。
这里主要说两个操作,一个是操作2,一个是操作4
如果A和B求相同的部分最终得到的全是A,证明A肯定包含在B内,或者A和B求全集为B,不含A的任何元素,也可以证明。这是判断子集的有效方式,当然,加上A!=B的条件之后可以判断是否为真子集。
操作4,还记得我们说的二进制数位的含义吗?这里就用到了。因为从1开始计数,所以只能左移i-1位,然后就对应到了一个二进制状态中的第几个元素,如果这个元素和状态与运算为1,证明这个元素存在,也就是第i位为1。
到了这里,我们终于解决了前置知识,可以开始进入动态规划了。
2、简单状压的思路
状态压缩,就是将原本看似不可能的枚举所有特定方案的做法,以二进制压缩的方式快速实现,状态压缩的题目一般来说都没有多项式级的解法,暴力算法的复杂度又会较高。状压的一般复杂度是
O
(
N
2
∗
2
n
)
\mathcal{O}(N^2*2^n)
O(N2∗2n)。虽然是特定问题的最优解,但是一般的数据范围不超过20。
我知道刚刚的那段话你们可能没太看懂,我们还是以一道例题来讲。
例题 原子弹
最近,火星研究人员发现了N个强大的原子。他们互相都不一样。
这些原子具有一些性质。当这两个原子碰撞时,其中一个原子会消失,产生大量的能量。
研究人员知道每两个原子在碰撞时的能释放的能量。
你要写一个程序,让它们碰撞之后产生最多的总能量。
输入格式
有多组数据。
每组数据下的第一行是整数N(2 <= N <= 10),这意味着有N个原子:A1到AN。
然后下面有N行,每行有N个整数。
在第i行中的第j个整数表示当i和j碰撞之后产生的能量,并且碰撞之后j会消失。
所有整数都是正数,且不大于10000。
输入以n=0结尾。
输入数据不超过500个。
输出格式
输出N个原子碰撞之后产生的最大总能量。
输入/输出例子1
输入:
2
0 4
1 0
3
0 20 1
12 0 1
1 10 0
0
输出:
4
22
2.1 例题分析
这道题的暴力算法相当的恐怖:我们需要枚举每两个原子弹的碰撞情况,而且还要枚举怎么碰撞的这个顺序,也就是N个原子弹的全排列,时间就是
O
(
N
!
∗
N
2
)
\mathcal{O}(N!*N^2)
O(N!∗N2)。这个复杂度显然是不能接受的。
这个题在枚举所有状态的时候时间太高了。那么我们有没有什么方法能快速枚举所有状态呢?
根据我们之前的集合知识,不难想出,一个集合有N个元素,完全可以映射为一个长度为N的二进制状态,而枚举这样的二进制状态只要
O
(
2
n
)
\mathcal{O}(2^n)
O(2n),远远小于阶乘的大小。
现在的第一个问题:如何设计状态?
对于一种可能的情况,一个二进制的1/0表示这个原子弹存在不存在,我们只需要用一重循环就可以得到一个状态下包含的所有与原子弹,显然,在
N
<
=
10
\mathcal{N}<=10
N<=10的情况下,我们两重循环挨个去炸是完全可行的。所以我们的状态直接设计为F[S]就行了,每个状态对应一个最大的保障能量,最后输出F[S] (S是总方案数)。
解决了状态设计,实际上方程还是很好推的。我们只需要在得到包含的原子弹后枚举所有可能的炸的情况就行了。因为这里分为谁炸完之后消失,所以对于“消失的原子弹”,我们就直接在状态中用异或运算剔除就可以了。
接下来让我们看一下DP的伪代码。
void DP(){
循环枚举所有状态S{
先收集状态中包含的原子弹 {
if(......)
boom[++d]= ...
}
两重循环遍历两两原子弹{
X号原子弹,Y号原子弹
1. 炸的时候使X消失
dp[s]=dp[s^X]+Energy[X][Y];
2. 炸的时候使Y消失
dp[s]=dp[s^Y]+Energy[Y][X];
}
}
输出最终方案DP[S]
}
这里注意一下我们的能量是有顺序的,对于相同的一组A,B,能量值Energy[A][B]和Energy[B][A]不一定是相等的。
接下来我们直接放代码,具体的注释代码里都都有。
2.2 完整代码
#include<bits/stdc++.h>
using namespace std;
const int N=12;
int n,Energy[N][N],dp[(1<<N)],boom[N];
/*
dp数组记录一个方案对应的最大能量
所以最多有2^n-1个方案 (从0~2^n-1)
那么2^n可以用连续左移n位完成(即*2*2*2*2...)
*/
void DP(){
int S=(1<<n)-1;//总方案数,2^n-1
for(int s=0;s<=S;++s){
int d=0;
for(int i=1;i<=n;++i)
if(s&(1<<(i-1)))//如果s第i位为1,那么第i个原子弹存在
boom[++d]=i;//收集原子弹
//这里注意,因为我们每次是直接炸一组,所以不需要重复枚举。
//如果每次只炸一个,那j也要从1开始,并且i需要枚举到n。
for(int i=1;i<d;++i)
for(int j=i+1;j<=d;++j){
if(i==j)//不能自己和自己炸
continue;
int a=boom[i],b=boom[j];//两颗原子弹
//b消失
dp[s]=max(dp[s],dp[s^(1<<(boom[j]-1))]+Energy[a][b]);
//a消失
dp[s]=max(dp[s],dp[s^(1<<(boom[i]-1))]+Energy[b][a]);
}
}
printf("%d\n",dp[S]);
}
int main(){
while(scanf("%d",&n)&&n!=0){
memset(dp,0,sizeof dp);
memset(Energy,0,sizeof Energy);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
scanf("%d",&Energy[i][j]);
DP();
}
return 0;
}
2.3 例题总结
以这道为基础,我们不难总结出状压DP的一些特点。
状压DP,我们首先要找到状态压缩的对象,根据这个对象去确定具体的DP状态设置。然后推出方程,以此解题。
一般来说,一道状压DP的题能状压的对象是固定的。因为状压对数据范围的要求及其严格。
3、基本状压DP的习题
这个部分讲述的6道题目都是基本的状压DP,我们一道一道分析。
3.1 O - Matching
有n本不同的书,编号1至n。
有n个不同的书包,编号1至n。
冬令营开始了,有n个学生,每个学生将会获得1个书包和1本书。
给出二维数组a[1…n][1…n],如果a[i][j]=1表示第i本书和第j个书包是兼容的,
若a[i][j]=0表示第i本书和第j个书包是不兼容的。
每个学生收到的1个书包和1本书必须是兼容的。
n本书和n个书包之间,有多少种不同的匹配方案。
输入格式
第一行,一个整数n. 1<=n<=21。
接下来是n行n列的二维数组a。
输出格式
一个整数,答案模1000000007。
输入/输出例子1
输入:
3
0 1 1
1 0 1
1 1 1
输出:
3
输入/输出例子2
输入:
4
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
输出:
1
输入/输出例子3
输入:
1
0
输出:
0
3.1.1 题目分析
这道题基本上和例题是一样的。
鉴于这道题数据很小,我们完全可以进行两重循环的枚举,每次判断书包和书是否兼容,兼容的话,就去判断书包是否存在于这个状态中。如果本来不存在,那么就加入这个新兼容的书包,然后计算结果。
这里值得注意的是,在这种顺序思考的思路之下(就是增加新的匹配),我们需要两个维度,一个维度枚举前i个书包,另一个维度枚举状态。
我们看看具体的操作。
void DP(){
两重循环枚举书包/书{
得到书的对应二进制
匹配?{
枚举所有可能状态{
if(这本书本来不在状态里&&上一个匹配状态成立){
dp[i][算上书本状态]+=dp[i-1][s];
}
}
}
}
}
我们先看看具体代码,这个实现比较简单。
//前i个书包,匹配状态为s,方案数
int S=(1<<n)-1;
dp[0]=1;
for(int i=1;i<=n;++i)//书包
for(int j=1;j<=n;++j){//书
int now=1<<(j-1);//得到书的对应二进制
if(a[i][j]){//新的兼容可能出现
for(int s=0;s<=S;++s)//枚举所有状态
if(dp[i-1][s]&&(s&now)==0)//新的书不在原状态里,并且前i-1个书包可以完成状态s的匹配
dp[i][(s|now)]=(dp[i][(s|now)]+dp[i-1][s])%MOD;//加上方案数
}
}
当然了,这个思路的大小是
O
(
N
2
∗
2
n
)
\mathcal{O}(N^2*2^n)
O(N2∗2n),虽然一般情况下已经很优秀,但是并不是最好的方法。
如果想要优化,我们只能在两重循环那里做文章,我们的
d
p
[
i
]
[
s
]
dp[i][s]
dp[i][s]是枚举到第i个书包状态为s的方案,我们原来的转移方程写成完整形式是:
d
p
[
i
]
[
s
∣
(
1
<
<
(
j
−
1
)
)
]
+
=
d
p
[
i
−
1
]
[
s
]
dp[i][s|(1<<(j-1))]+=dp[i-1][s]
dp[i][s∣(1<<(j−1))]+=dp[i−1][s]
然后我们会发现,
s
s
s一定是
s
∣
(
1
<
<
(
j
−
1
)
)
s|(1<<(j-1))
s∣(1<<(j−1))的子集。
也就是说,我们顺着考虑可行的情况下,现在我们可以进行逆向方程推导。也就是说:
d
p
[
i
]
[
s
]
+
=
d
p
[
i
−
1
]
[
s
−
1
<
<
(
j
−
1
)
]
dp[i][s]+=dp[i-1][s-1<<(j-1)]
dp[i][s]+=dp[i−1][s−1<<(j−1)] 这个方程是可行的。
那么我们还可以按照之前方法枚举着做,但是因为
s
−
1
<
<
(
j
−
1
)
s-1<<(j-1)
s−1<<(j−1)一定是
s
s
s的子集,所以,我们完全就可以省略
i
i
i的枚举而先对状态进行枚举,所以这样,整个代码结构又回到了我们熟悉的样子:
void DP(){
循环枚举所有状态s{
算出状态中存在有多少个书包
循环枚举书{
得到书的对应二进制
if(书如果匹配的状态存在&&当前的书包和书兼容)
dp[s]+=dp[s^书的匹配状态]
}
}
}
我知道你们肯定和我一样,非常的疑惑。我先给个对应代码,然后再讲。
for(int s=0;s<=S;++s){
int cnt=Count(s);
for(int i=1;i<=n;++i){
int st=(1<<(i-1));
if(s&st&&a[cnt][i])
dp[s]=(dp[s]+dp[s^st])%MOD;
}
}
首先就是这个“算出状态中存在的书包”,实际上对应的操作就是这个
C
o
u
n
t
(
s
)
Count(s)
Count(s),统计状态s中有多少个1。然后最大的问题就出来了,如果
C
o
u
n
t
(
s
)
Count(s)
Count(s)是统计多少个1的话,那么这个
i
f
if
if就怎么看怎么不合理啊?
为什么会拿这个
c
n
t
cnt
cnt的个数和书作匹配啊?
这里是个非常隐蔽的条件。如果我的书包和书在一种状态下是匹配的,那么还可能打乱顺序进行匹配。好比原来书包按照1 2 3 4 5匹配了,那么打乱顺序按照2 3 1 4 5对于相同的学生就又是一种方案。而如果你去看我们优化思路时的状态设置,会发现这个状态枚举时已经暗含了顺序的打乱。110和101对应两种不同的二进制。
所以枚举到状态
s
s
s的时候,以1的个数确定找的是第几个书包匹配,我们始终去找一本书和这第
C
o
u
n
t
(
s
)
Count(s)
Count(s)个书包作匹配,这样随着状态的枚举,1的个数只要没有增加,对应的就是这第
C
o
u
n
t
(
s
)
Count(s)
Count(s)个书包位置被打乱的所有可能。
然后就是需要判断这个书包本身的位置,如果虽然它和这本书匹配,但是这个匹配不在状态里,那也不能要。
所以,这道题解决了。后面的转移过程和例题类似,我不讲了。
下面给不优化和优化的两版代码。
3.1.2 完整代码
不优化版
#include<bits/stdc++.h>
using namespace std;
const int N=50;
const int MOD=1000000007;
int n;
int a[N][N],dp[(1<<23)];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
scanf("%d",&a[i][j]);
//前i个书包,匹配状态为s,方案数
int S=(1<<n)-1;
dp[0]=1;
for(int i=1;i<=n;++i)//书包
for(int j=1;j<=n;++j){//书
int now=1<<(j-1);//得到书的对应二进制
if(a[i][j]){//新的兼容可能出现
for(int s=0;s<=S;++s)//枚举所有状态
if(dp[i-1][s]&&(s&now)==0)//新的书不在原状态里,并且前i-1个书包可以完成状态s的匹配
dp[i][(s|now)]=(dp[i][(s|now)]+dp[i-1][s])%MOD;//加上方案数
}
}
printf("%d\n",dp[S]);
return 0;
}
优化版
#include<bits/stdc++.h>
using namespace std;
const int N=50;
const int MOD=1000000007;
int n;
int a[N][N],dp[(1<<23)];
int Count(int x){
int res=0;
while(x){
x=x&(x-1);
++res;
}
return res;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
scanf("%d",&a[i][j]);
//匹配状态为s,方案数
int S=(1<<n)-1;
dp[0]=1;
//双重枚举时间很大,逆推方程进行优化
for(int i=0;i<=S;++i){//枚举所有状态
int cnt=Count(i);//当前是第几个书包
for(int j=1;j<=n;++j){//枚举数
int st=(1<<(j-1));
if(i&st&&a[cnt][j])//如果书和书包匹配,同时这本书和书包匹配之后在状态里
dp[i]=(dp[i]+dp[i^st])%MOD; //转移
}
}
printf("%d\n",dp[S]);
return 0;
}
3.2 U - Grouping
有n只兔子,编号1至n。
给出二维数组a[1…n][1…n]其中a[i][j]表示第i只兔子和第j只兔子的兼容度,
数据保证a[i][i]=0, a[i][j] = a[j][i]。
现在你需要把这n只兔子分成若干组,使得每只兔子仅属于一个组。
当分组结束后,对于1<=i<j<=n,你将会获得a[i][j]元钱,前提是第i只兔子和第j只兔子分在了同一组。
应该如何分组,才能使得最终赚的钱最多。
输入格式
第一行,一个整数n。 1<=n<=16。
接下来是二维数组a, 其中 -1e9 <= a[i][j] <= 1e9。
输出格式
一个整数,最多能赚的钱。
输入/输出例子1
输入:
3
0 10 20
10 0 -100
20 -100 0
输出:
20
输入/输出例子2
输入:
2
0 -10
-10 0
输出:
0
输入/输出例子3
输入:
4
0 1000000000 1000000000 1000000000
1000000000 0 1000000000 1000000000
1000000000 1000000000 0 -1
1000000000 1000000000 -1 0
输出:
4999999999
3.2.1 题目分析
这个题目我感觉不用多说了,和之前的题目稍微有区别。
我们尝试枚举出每种状态只分1组的情况,然后类似于偏序的题目,枚举分割的端点进行转移就行了。注意这里的分割断点是每种状态里1的位置,所以每次去掉最后一个1就行了。
我直接给代码,看注释吧。
3.2.2 完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=17;
int n,a[N][N];
ll f[(1<<20)],v[(1<<20)];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
scanf("%d",&a[i][j]);
ll S=(1<<n)-1;
//求出每种状态不分组(只有1组)的兼容度
for(int s=1;s<=S;++s){//枚举所有状态
//直接暴力枚举任意两只兔子
for(int i=1;i<=n;++i)
for(int j=i+1;j<=n;++j){
ll m1=1<<(i-1),m2=1<<(j-1);
if((s&m1)==m1&&(s&m2)==m2)//两只兔子都在状态s里
v[s]+=a[i][j];//加上兼容度
}
}
for(int s=1;s<=S;++s){//枚举所有状态
f[s]=v[s];
for(int i=s&(s-1);i;i=(i-1)&s)//根据状态枚举断点
f[s]=max(f[s],f[i]+f[s^i]);//打擂台转移
}
printf("%lld\n",f[S]);//输出
return 0;
}
3.3 开锁
有n把锁,编号1至n。有m把钥匙,第i把钥匙的价格是p[i],第i把钥匙可以开k[i]把锁,
分别可以开第c[i][1],c[i][2],…第c[k[i]]把锁。
问你如果购买钥匙,用最少的费用把n把锁全部打开。
如果无论无何也不能把n把锁全部打开,输出-1。
输入格式
第一行,两个整数n和m。1<=n<=12, 1<=m<=1000。
接下来是描述m把钥匙的信息,第i把钥匙有两行:
第1行,两个整数: p[i]和k[i]。1<=p[i]<=100000, 1<=k[i]<=n。
第2行,k[i]个整数,依次表似乎第i把钥匙所能打开的锁的编号,从小到大给出编号。
输出格式
一个整数。
输入/输出例子1
输入:
2 3
10 1
1
15 1
2
30 2
1 2
输出:
25
输入/输出例子2
输入:
12 1
100000 1
2
输出:
-1
输入/输出例子3
输入:
4 6
67786 3
1 3 4
3497 1
2
44908 3
2 3 4
2156 3
2 3 4
26230 1
2
86918 1
3
输出:
69942
3.3.1 题目分析
这道题目还是挺有意思的。
首先我们很明显能知道状压的只能是
n
n
n把锁的状态,但是现在的问题是怎么安排拿什么钥匙开锁的最小花费呢?
这个最小花费,当时给我的感觉是类似背包一样的操作,事实证明我是对的。但是这个思路确实有点烧脑。
我们要想让
n
n
n把锁全部最小花费打开,那就暴力试就行了。鉴于一把钥匙可能开很多锁,我枚举所有可能的锁的状态,然后只要是这把钥匙能开的全部置为1。结合之前的状态的花费+这把钥匙的花费,就是从之前的状态转移到用这把钥匙开锁之后的状态。
写成方程就是
d
p
[
s
∣
k
e
y
]
=
m
i
n
(
d
p
[
s
∣
k
e
y
]
+
∑
s
=
1
(
1
<
<
n
)
−
1
m
i
n
(
d
p
[
s
]
+
p
[
i
]
)
)
dp[s|key]=min(dp[s|key]+\sum_{s=1}^{(1<<n)-1}min(dp[s]+p[i]))
dp[s∣key]=min(dp[s∣key]+∑s=1(1<<n)−1min(dp[s]+p[i]))
那么我们现在就只需要得到这把钥匙能开的所有的锁的状态
k
e
y
key
key就行了。
这个实际上也很好求,把整个
k
e
y
key
key映射为一个二进制状态,能开的锁为1,不然为0。这样就满足了我们的上述条件。
3.3.2 完整代码
这个题目我也直接给代码。各位自己看注释。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int p[N],k[N];
int c[N][20],dp[N];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d%d",&p[i],&k[i]);
for(int j=1;j<=k[i];++j)
scanf("%d",&c[i][j]);
}
for(int i=0;i<=(1<<n);++i)//这里要求最小花费,所以初始化无穷大
dp[i]=1e9;
dp[0]=0;
for(int i=1;i<=m;++i){//枚举所有钥匙
int now=0;
for(int j=1;j<=k[i];++j)//映射能开的锁
now |= (1<<(c[i][j]-1));
/*
这里按照背包的写法,倒着枚举,但是正着枚举也可以。
显然,如果一个数和一个数重复或两次,那么第二次的结果肯定和第一次的结果相同,所以可行。
*/
for(int s=(1<<n-1);s>=0;--s){//枚举所有锁的状态
int nxt=s|now;
dp[nxt]=min(dp[nxt],dp[s]+p[i]);//向新的状态转移
}
}
if(dp[(1<<n)-1]!=1e9)//更新到全开的状态,有结果
printf("%d\n",dp[(1<<n)-1]);
else
printf("-1\n");
return 0;
}
3.4 旅行商
有三维立体空间里,有n个城市,第i个城市的坐标是(x[i],y[i],z[i])。
从第i个城市到第j个城市的距离dis[i][j] = abs(x[j]-x[i]) + abs(y[j]-y[i]) + max(0,z[j]-z[i]),其中abs是求绝对值。
你需要从1号城市出发,遍历每一个城市至少一次,最后回到1号城市,问最少的旅行距离。
输入格式
第一行,一个整数n。2<=n<=17。
接下来有n行,第i行有三个整数:x[i],y[i],z[i]。-1e6<=x[i],y[i],z[i]<=1e6。
所有的城市坐标不会重叠。
输出格式
一个整数。
输入/输出例子1
输入:
2
0 0 0
1 2 3
输出:
9
输入/输出例子2
输入:
3
0 0 0
1 1 1
-1 -1 -1
输出:
10
输入/输出例子3
输入:
17
14142 13562 373095
-17320 508075 68877
223606 -79774 9979
-24494 -89742 783178
26457 513110 -64591
-282842 7124 -74619
31622 -77660 -168379
-33166 -24790 -3554
346410 16151 37755
-36055 51275 463989
37416 -573867 73941
-3872 -983346 207417
412310 56256 -17661
-42426 40687 -119285
43588 -989435 -40674
-447213 -59549 -99579
45825 7569 45584
输出:
6519344
3.4.1 题目分析
这道题目是状态压缩经典题的一个升级版,原题是直接给了两两城市之间的距离。
显然,状压的对象很明显:只能是城市的情况,那么枚举排列情况是不现实的。我们枚举到达了那些城市就行了。
然后这道题就类似于
F
l
o
y
d
Floyd
Floyd,或者说是偏序DP,我们不妨设状态为
d
p
[
s
]
[
i
]
dp[s][i]
dp[s][i],表示状态为s,最终到达城市i的最小距离。那么接下来只需要挨个枚举每个结尾和对应的状态,并从中枚举途径城市进行转移就行了。
那么易得伪代码如下:
void DP(){
枚举所有的途径城市状态s{
枚举所有的结尾i{
if(i存在于状态s中){
枚举所有的途径城市j
dp[s][i]=min(dp[s][i],dp[s][j]+dis[j][i]);
}
}
}
}
这道题实际上思路不难,但是坑点是最后的求答案过程,根据我们的方程设定,不难想出最终答案是
∑
i
=
1
n
m
i
n
(
d
p
[
S
]
[
i
]
)
\sum_{i=1}^{n}min(dp[S][i])
∑i=1nmin(dp[S][i]),但是由于我们以第
i
i
i个城市结尾,所以最终还要加上这个城市到1的距离!!!
接下来还是直接给完整代码。
3.4.2 完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=20;
ll n;
struct node{
ll x,y,z;
}a[N];
ll dp[(1<<N)][N],dis[N][N];
void dist(){//计算任意两个城市之间的距离
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
//!
dis[j][i]=abs(a[j].x-a[i].x)+abs(a[j].y-a[i].y)+max(ll(0),a[j].z-a[i].z);
}
void DP(){
memset(dp,0x3f3f3f3f,sizeof dp);
dp[1][1]=0;
ll S=(1<<n)-1;
for(ll s=1;s<=S;++s){//枚举状态s
ll si=0,sj=0;
for(ll i=1;i<=n;++i){//枚举终点
si=1<<(i-1),sj=0;
if((s&si))//终点存在才操作
for(ll j=1;j<=n;++j){//枚举中间点
sj=1<<(j-1);
if(j!=i&&(s&sj))//中间点也存在,同时不能使终点
dp[s][i]=min(dp[s][i],dp[s^si][j]+dis[j][i]);//正常计算
}
}
}
ll ans=0x7fffffff;
for(int i=2;i<=n;++i)
ans=min(ans,dp[S][i]+dis[i][1]);//!!!一定要加上返回1的距离
printf("%lld\n",ans);
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;++i)
scanf("%lld%lld%lld",&a[i].x,&a[i].y,&a[i].z);
dist();
DP();
return 0;
}
3.5 不同排列
有n个学生,学号1至n。你现在需要把这n个学生从左往右排成一行形成队伍,要满足如下所有m个条件:
第i个条件的格式是x[i],y[i],z[i],表示队伍的前x[i]学生当中,学号小于y[i]的学生不能超过z[i]人。
求满足上面所有m个条件的队伍有多少种不同的方案。
输入格式
第一行,n和m。 2<=n<=18, 0<=m<=100。、
接下来m行,第i行是x[i],y[i],z[i]。1<=x[i],y[i]<n,0<=z[i]<n。
输出格式
一个整数。
输入/输出例子1
输入:
3 1
2 2 1
输出:
4
输入/输出例子2
输入:
5 2
3 3 2
4 4 3
输出:
90
输入/输出例子3
输入:
18 0
输出:
6402373705728000
3.5.1 题目分析
乍一看,这个题目除了个数据范围,完全没有一点状压的影子。
怎么设置状态???
d
p
[
s
]
dp[s]
dp[s]怎么能表示排列呢?
哎,别急。仔细去想一想,这道题的表示方式完全可以借鉴第一题啊。
d p [ s ] dp[s] dp[s]表示状态为s,选择Count(s)个人时的排列方案。
这个Count(s)我们还是用第一题的理解:状态s中有多少个人。
然后如果我们知道到达每个位置所需要满足的限制条件,我们就可以直接判定这个状态本身的合法性,如果这个状态合法,那么又一次采取断点枚举操作,我们枚举集合中的剔除每一个元素后的方案数,就是这个状态下所有可能的方案数。
举个例子,当前状态是10011,我们假设状态合法,那么对于这个状态的所有方案就是:
d
p
[
10011
]
=
d
p
[
00011
]
+
d
p
[
10001
]
+
d
p
[
10010
]
dp[10011]=dp[00011]+dp[10001]+dp[10010]
dp[10011]=dp[00011]+dp[10001]+dp[10010]
对于固定的一个元素以及固定的方案,去除这个元素的结果和加上这个元素的结果是一样的。
我还是先给伪代码。
void DP(){
枚举所有状态s{
统计s当中1的个数,算出当前到第几个人
if(状态合法){
循环找出每一个s中的元素
dp[s]+=dp[s^s中的一个元素]
}
}
}
但是现在还有个BUG,怎么知道状态是否合法呢?
首先,我们肯定要知道到达第
i
i
i位的条件限制。
因为输入给了前
x
x
x个人学号
<
y
<y
<y的限制人数
z
z
z,我们不妨就记为
l
i
m
[
x
]
[
y
−
1
]
=
z
lim[x][y-1]=z
lim[x][y−1]=z。这样的话,在状态s中人数固定的情况下,我们只需要判断每一个位i前面所含有的
<
=
y
−
1
<=y-1
<=y−1的人数是否超过限制就行了。
这种判断方法可行,是因为我们枚举每一位的时候实际上就在枚举学号,直接就能判断。
直接给代码了啊
bool check(ll nn,ll sta){//nn是固定人数,sta是我们要检查的状态
ll t=0;//记录人数
for(ll i=1;i<=n;++i){//循环遍历每一个人
ll si=1<<(i-1);
if(sta&si) ++t;//存在,人数++
if(t>lim[nn][i-1])//如果超过了学号限制
return false;//不合法
}
return true;//合法
}
前期的读入处理也很简单,直接贴代码:
for(ll i=1;i<=m;++i){
scanf("%lld%lld%lld",&x,&y,&z);
lim[x][y-1]=min(lim[x][y-1],z);//注意这里打一个最小值,可能会重复读入,取要求最严的那个
}
3.5.2 完整代码
我知道你在期待什么
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=20;
ll n,m;
ll x,y,z;
ll lim[N][N],dp[(1<<N)];
bool check(ll nn,ll sta){//nn是固定人数,sta是我们要检查的状态
ll t=0;//记录人数
for(ll i=1;i<=n;++i){//循环遍历每一个人
ll si=1<<(i-1);
if(sta&si) ++t;//存在,人数++
if(t>lim[nn][i-1])//如果超过了学号限制
return false;//不合法
}
return true;//合法
}
void DP(){
dp[0]=1;
ll S=(1<<n)-1;
for(ll s=1;s<=S;++s){//枚举所有状态
ll si=0,cnt=0;
for(ll i=1;i<=n;++i){//求出当前的队伍长度
si=1<<(i-1);
if(s&si)
++cnt;
}
if(check(cnt,s)){//判断合法性
for(ll i=1;i<=n;++i){
si=1<<(i-1);//存在就转移
if((si&s))
dp[s]+=dp[s^si];
}
}
}
printf("%lld\n",dp[S]);
}
int main(){
memset(lim,0x3f3f3f3f,sizeof lim);
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=m;++i){
scanf("%lld%lld%lld",&x,&y,&z);
lim[x][y-1]=min(lim[x][y-1],z);//注意这里打一个最小值,可能会重复读入,取要求最严的那个
}
DP();
return 0;
}
结语——
这只是最基础的状压DP,但是我居然还有两道题没讲(大悲)。
预告一下啊,后面大概率会有3篇题解:一篇解决遗留的两道题,一篇是轮廓线状压DP,一篇是树形DP(这个玩意简单一点)。
状压DP,就是要无惧时间复杂度,先从最暴力的开始想起,然后看见全排列的出现基本上就AC预定了。只要再将全排列部分用状压优化即可。它属于一种优化型的DP,我个人认为可以放到线段树和单调队列那部分去。
U p d a t e 2022.8.22 Update 2022.8.22 Update2022.8.22:修改了部分笔误,增添了差集的描述,并对程序进行调整和说明