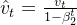优化算法是机器学习和深度学习模型训练中至关重要的部分。本文将详细介绍Adam(Adaptive Moment Estimation)和RMSprop(Root Mean Square Propagation)这两种常用的优化算法,包括它们的原理、公式和具体代码示例。
RMSprop算法
RMSprop算法由Geoff Hinton提出,是一种自适应学习率的方法,旨在解决标准梯度下降在处理非平稳目标时的问题。其核心思想是对梯度的平方值进行指数加权平均,并使用这个加权平均值来调整每个参数的学习率。
RMSprop算法公式
-
计算梯度:
其中,
是第
次迭代时的梯度,
是损失函数,
是当前参数。
-
计算梯度的平方和其指数加权平均值:
其中,
是梯度平方的指数加权平均,
是衰减率,通常取值为0.9。
-
更新参数:
其中,
是学习率,
是为了防止除零的小常数,通常取值为
。
RMSprop算法的实现
下面是用Python和TensorFlow实现RMSprop算法的代码示例:
import tensorflow as tf
# 初始化参数
learning_rate = 0.001
rho = 0.9
epsilon = 1e-08
# 创建RMSprop优化器
optimizer = tf.keras.optimizers.RMSprop(learning_rate=learning_rate, rho=rho, epsilon=epsilon)
# 定义模型和损失函数
model = tf.keras.Sequential([...]) # 定义你的模型
loss_fn = tf.keras.losses.MeanSquaredError()
# 编译模型
model.compile(optimizer=optimizer, loss=loss_fn)
# 训练模型
model.fit(train_data, train_labels, epochs=10)
Adam算法
Adam算法结合了RMSprop和动量(Momentum)的思想,是一种自适应学习率优化算法。Adam算法在处理稀疏梯度和非平稳目标时表现出色,因此被广泛应用于深度学习模型的训练中。
Adam算法公式
-
计算梯度:
-
计算梯度的一阶矩估计和二阶矩估计的指数加权平均值:
其中,
是梯度的一阶矩估计,
是梯度的二阶矩估计,
和
分别是动量和均方根的衰减率,通常取值为0.9和0.999。
-
进行偏差校正:
-
更新参数:
Adam算法的实现
下面是用Python和TensorFlow实现Adam算法的代码示例:
import tensorflow as tf
# 初始化参数
learning_rate = 0.001
beta_1 = 0.9
beta_2 = 0.999
epsilon = 1e-08
# 创建Adam优化器
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate, beta_1=beta_1, beta_2=beta_2, epsilon=epsilon)
# 定义模型和损失函数
model = tf.keras.Sequential([...]) # 定义你的模型
loss_fn = tf.keras.losses.MeanSquaredError()
# 编译模型
model.compile(optimizer=optimizer, loss=loss_fn)
# 训练模型
model.fit(train_data, train_labels, epochs=10)
总结
RMSprop和Adam都是深度学习中常用的优化算法,各自有其优势。RMSprop通过调整每个参数的学习率来处理非平稳目标,而Adam则结合了动量和均方根的思想,使得它在处理稀疏梯度和非平稳目标时表现优异。理解并灵活运用这些优化算法,将有助于提高模型训练的效率和效果。
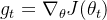
![E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g_t^2](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9FJTVCZyU1RTIlNURfdA%3D%3D%20%3D%20%5Cgamma%20E%5Bg%5E2%5D_%7Bt-1%7D%20+%20%281%20-%20%5Cgamma%29%20g_t%5E2)