在强化学习(Reinforcement Learning, RL)中,价值函数的估计是核心任务之一。蒙特卡洛(Monte Carlo, MC)方法和时序差分(Temporal Difference, TD)方法是两种常用的策略,用于估计状态值函数(Value Function)。本文将详细介绍这两种算法的原理、应用场景以及它们之间的对比,并通过代码示例展示它们的实际应用。
蒙特卡洛算法
原理
蒙特卡洛方法通过多次采样完整的序列来估计价值函数。每次从初始状态开始,直到达到终止状态,并根据每个状态序列的回报(Reward)来更新状态值。
给定一个策略 
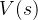
其中 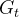
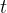
其中 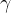
是未来的回报。
实战示例
以下是一个使用蒙特卡洛方法进行价值估计的简单示例:
import numpy as np
# 环境参数
num_states = 5
num_episodes = 1000
gamma = 0.9
# 随机策略
def random_policy(state):
return np.random.choice([0, 1])
# 环境
def env_step(state, action):
if state == num_states - 1:
return state, 0
next_state = state + 1 if action == 1 else state
reward = 1 if next_state == num_states - 1 else 0
return next_state, reward
# 蒙特卡洛价值估计
value_estimates = np.zeros(num_states)
returns = {state: [] for state in range(num_states)}
for _ in range(num_episodes):
state = 0
episode = []
while state != num_states - 1:
action = random_policy(state)
next_state, reward = env_step(state, action)
episode.append((state, action, reward))
state = next_state
G = 0
for state, _, reward in reversed(episode):
G = reward + gamma * G
returns[state].append(G)
value_estimates[state] = np.mean(returns[state])
print("状态值估计:", value_estimates)
时序差分算法
原理
时序差分方法结合了蒙特卡洛方法和动态规划的优点,可以在没有模型的情况下进行在线学习。TD(0) 是最简单的时序差分方法,它更新状态值函数 $V(s)$ 的公式为:
其中 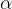
是即时奖励,
是下一状态。
实战示例
以下是一个使用时序差分方法进行价值估计的简单示例:
import numpy as np
# 环境参数
num_states = 5
num_episodes = 1000
gamma = 0.9
alpha = 0.1
# 随机策略
def random_policy(state):
return np.random.choice([0, 1])
# 环境
def env_step(state, action):
if state == num_states - 1:
return state, 0
next_state = state + 1 if action == 1 else state
reward = 1 if next_state == num_states - 1 else 0
return next_state, reward
# 时序差分价值估计
value_estimates = np.zeros(num_states)
for _ in range(num_episodes):
state = 0
while state != num_states - 1:
action = random_policy(state)
next_state, reward = env_step(state, action)
value_estimates[state] += alpha * (reward + gamma * value_estimates[next_state] - value_estimates[state])
state = next_state
print("状态值估计:", value_estimates)
对比
-
更新方式:
- 蒙特卡洛方法:仅在一个完整的序列结束后进行更新,需要等待一个回合结束才能得到状态值的估计。
- 时序差分方法:可以在每一步进行更新,不需要等待整个回合结束,更适合在线学习。
-
方差与偏差:
- 蒙特卡洛方法:通常有较高的方差,但无偏估计。
- 时序差分方法:通常有较低的方差,但可能有偏差。
-
计算效率:
- 蒙特卡洛方法:计算量较大,适合离线处理和最终状态明确的任务。
- 时序差分方法:计算量较小,适合在线处理和实时更新。
-
适用场景:
- 蒙特卡洛方法:适用于回报能够在有限时间内观察到的环境。
- 时序差分方法:适用于回报在未来不确定时间内才能完全观察到的环境。
总结
蒙特卡洛方法和时序差分方法各有优缺点,在不同的应用场景下可以互为补充。蒙特卡洛方法通过完全序列的回报估计状态值,适用于离线处理;时序差分方法通过每一步的即时回报和估计值更新状态值,适合在线学习和实时更新。在实际应用中,可以根据具体需求选择合适的方法,甚至可以结合使用,以达到最优的价值估计效果。
![V(s) = \mathbb{E}_\pi[G_t | S_t = s]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9WJTI4cyUyOQ%3D%3D%20%3D%20%5Cmathbb%7BE%7D_%5Cpi%5BG_t%20%7C%20S_t%20%3D%20s%5D)

![V(s) \leftarrow V(s) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(s)]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9WJTI4cyUyOQ%3D%3D%20%5Cleftarrow%20V%28s%29%20+%20%5Calpha%20%5BR_%7Bt+1%7D%20+%20%5Cgamma%20V%28S_%7Bt+1%7D%29%20-%20V%28s%29%5D)