1 链、路、圈、回路
1.1 链和路的概念、区别、关系
链是连接两个节点的一序列边或弧;
路是连接两个节点的同一方向上的一序列边或弧;
区别:链和路的区别仅在于链是无方向限制的,路是同一方向的;
关系:①路是沿前进方向连接所有弧的链;②一个节点序列如果是路,那么一定也是链;③一个节点序列如果是链,那么不一定也是路;
1.2 圈和回路的概念、区别、关系
圈是起点和终点相同的一条链;
回路是起点和终点相同的一条路;
区别:与链和路的区别一致,仅在于圈是无方向限制的,回路是同一方向的;
关系:①与链和路的关系一致,回路是所有弧均沿同一方向的圈;②一个节点序列如果是回路,那么一定也是圈;③一个节点序列如果是圈,那么一定也是回路;
1.3 链、路、圈、回路例题
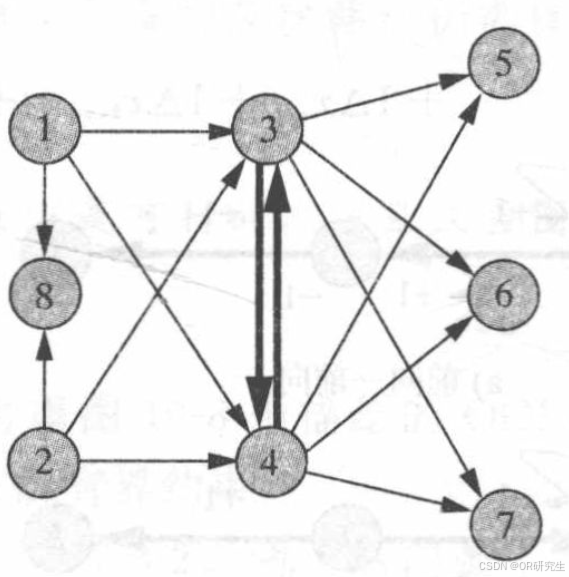
节点1到节点5的链:1-3-5,1-3-4-5,1-8-2-3-5,1-8-2-4-5,1-8-2-4-3-5;
节点1到节点5的路:1-3-5,1-3-4-5;
包含节点1和节点5的圈:1-3-5-4-1,1-8-2-4-5-3-1;
没有包含节点1和节点5的回路;
那么我们好奇了,只有两个节点能组成的路、链、圈、回路吗?答案是可以的。如例题所示,节点序列3-4-3既是链和圈,也是路和回路。
2 树与生成树
连通图:若一个图的每对节点间都存在一条链,则我们称该图是连通的。
树:若一个图是连通的,且不包含圈,则它是一个树。
为什么我们会有树的概念呢?因为树拥有一条重要且广泛实用的性质:树上的每对节点都由唯一的一条链相连。
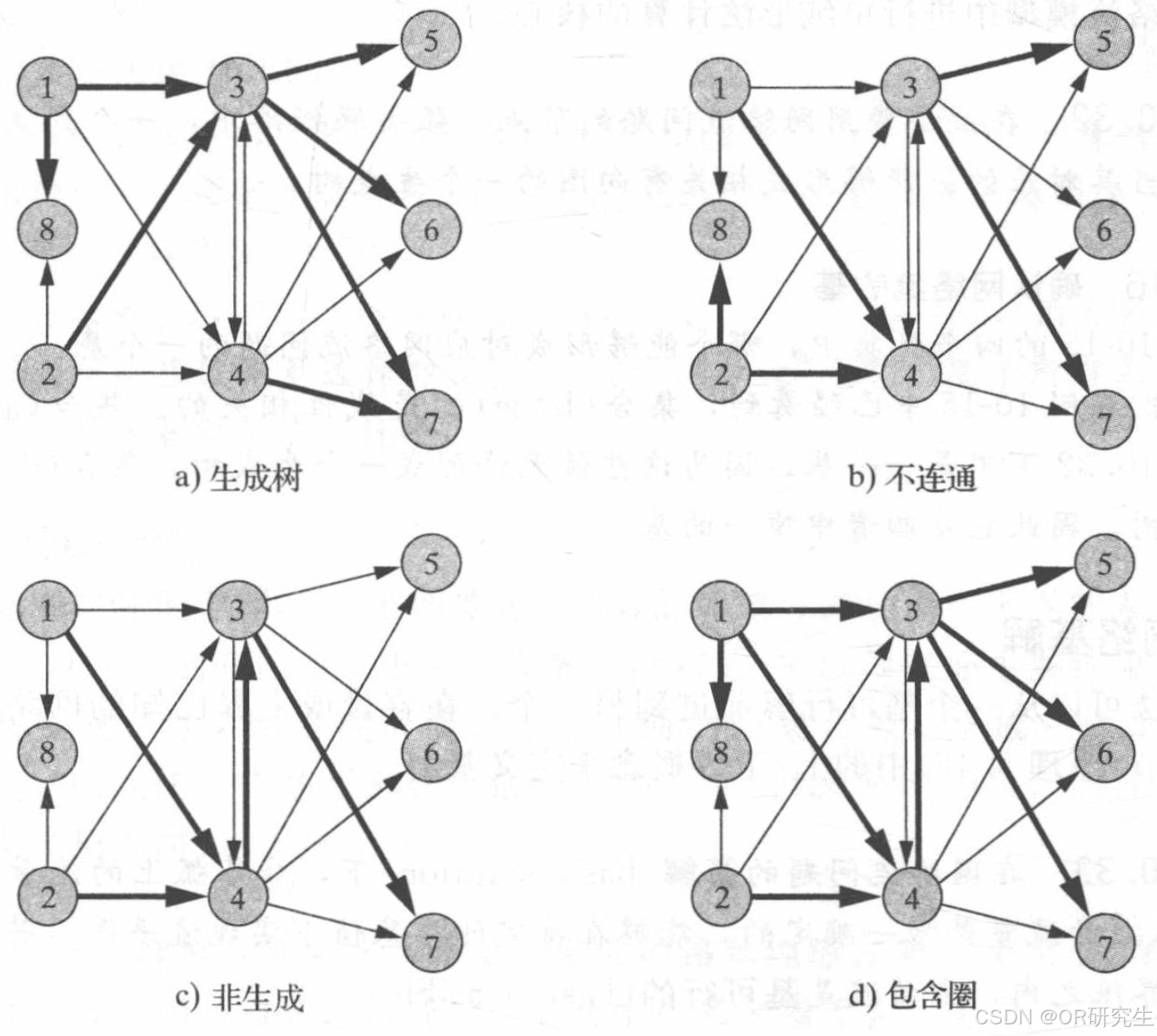
生成树:若一个树连接了图中的每个节点,则它是一个生成树。生成树就是从一个图中提取的连接所有节点的树;
生成树的概念更常用的原因是我们在现实问题中经常需要从网络中提取最小生成树问题,也是数据结构中的重要问题。
如上图所示,a)是这个图的生成树;b)节点之间没有连通;c)没有连接图中的所有节点,所以不生成;d)包含圈,所以不是树,也不是生成树。