一、线索二叉树原理
前面介绍二叉树原理及特殊二叉树文章中提到,二叉树可以使用两种存储结构:顺序存储和二叉链表。在使用二叉链表的存储结构的过程中,会存在大量的空指针域,为了充分利用这些空指针域,引申出了“线索二叉树”。回顾一下二叉链表存储结构,如下图:
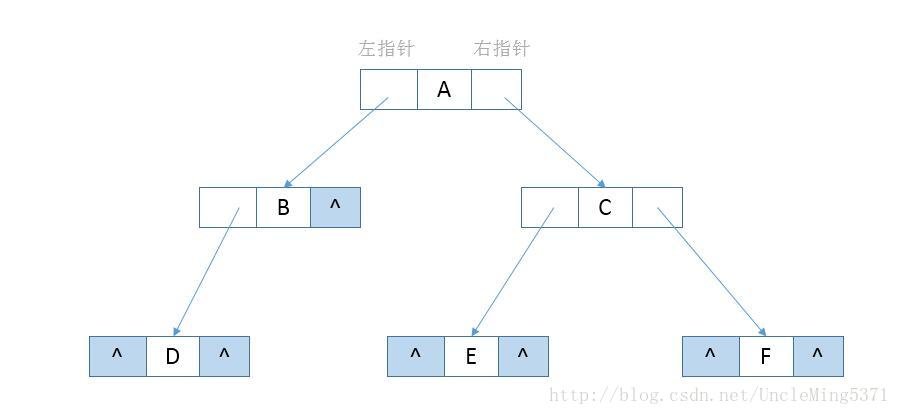
通过观察上面的二叉链表,存在着若干个没有指向的空指针域。对于一个有n个节点的二叉链表,每个节点有指向左右节点的2个指针域,整个二叉链表存在2n个指针域。而n个节点的二叉链表有n-1条分支线,那么空指针域的个数=2n-(n-1) = n+1个空指针域,从存储空间的角度来看,这n+1个空指针域浪费了内存资源。
从另外一个角度来分析,如果我们想知道按中序方式遍历二叉链表时B节点的前驱节点或者后继节点时,必须要按中序方式遍历二叉链表才能够知道结果,每次需要结果时都需要进行一次遍历,是否可以考虑提前存储这种前驱和后继的关系来提高时间效率呢?
综合以上两方面的分析,可以通过充分利用二叉链表中的空指针域,存放节点在某种遍历方式下的前驱和后继节点的指针。 我们把这种指向前驱和后继的指针成为线索,加上线索的二叉链表成为线索链表,对应的二叉树就成为“线索二叉树(Threaded Binary Tree)” 。
二、构建线索二叉树过程
1、我们对二叉树进行中序遍历(不了解二叉树遍历请参考二叉树及特殊二叉树介绍),将所有的节点右子节点为空的指针域指向它的后继节点。如下图:
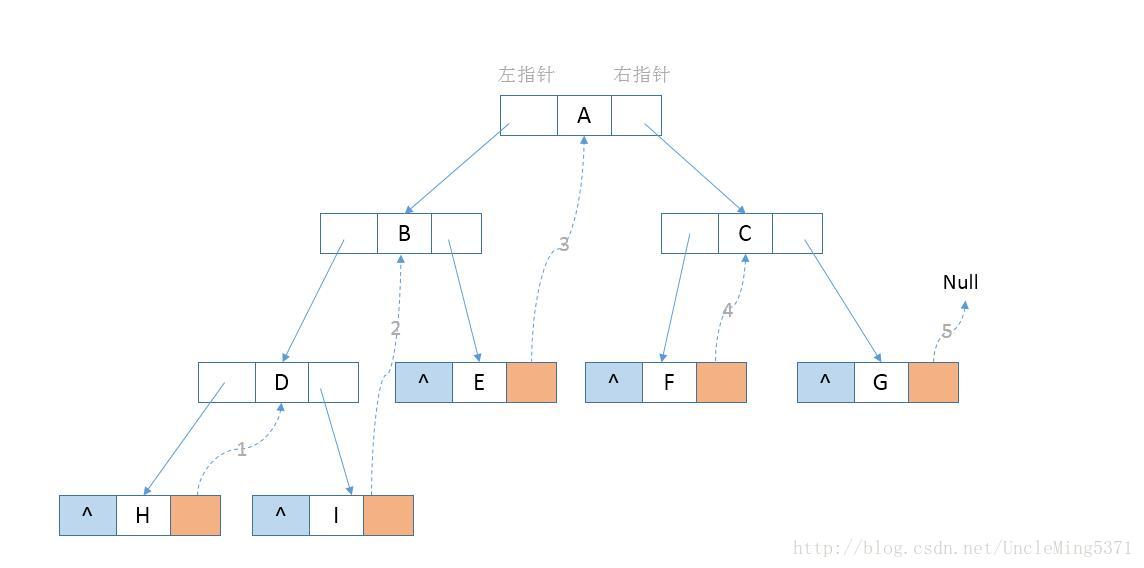
通过中序遍历我们知道H的right指针为空,并且H的后继节点为D(如上图第1步),I的right指针为空,并且I的后继节点为B(如上图第2步),以此类推,知道G的后继节点为null,则G的right指针指向null。
2、接下来将这颗二叉树的所有节点左指针域为空的指针域指向它的前驱节点。如下图:
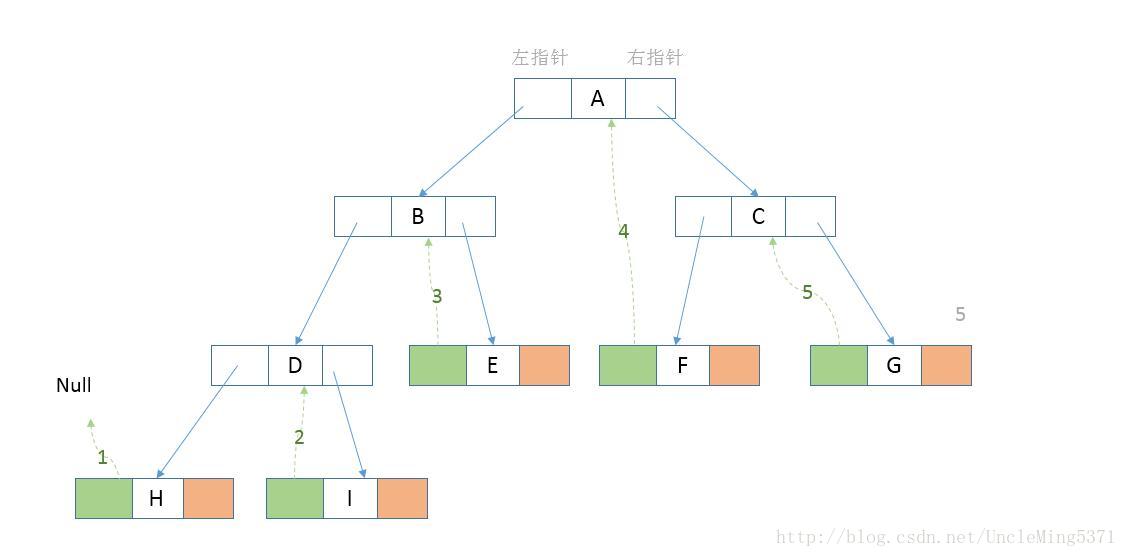
如上图,H的left指针域指向Null(如第1步),I的前驱节点是D,则I的left指针指向D,以此类推。
通过上面两步完成了整个二叉树的线索化,最后结果如下图:
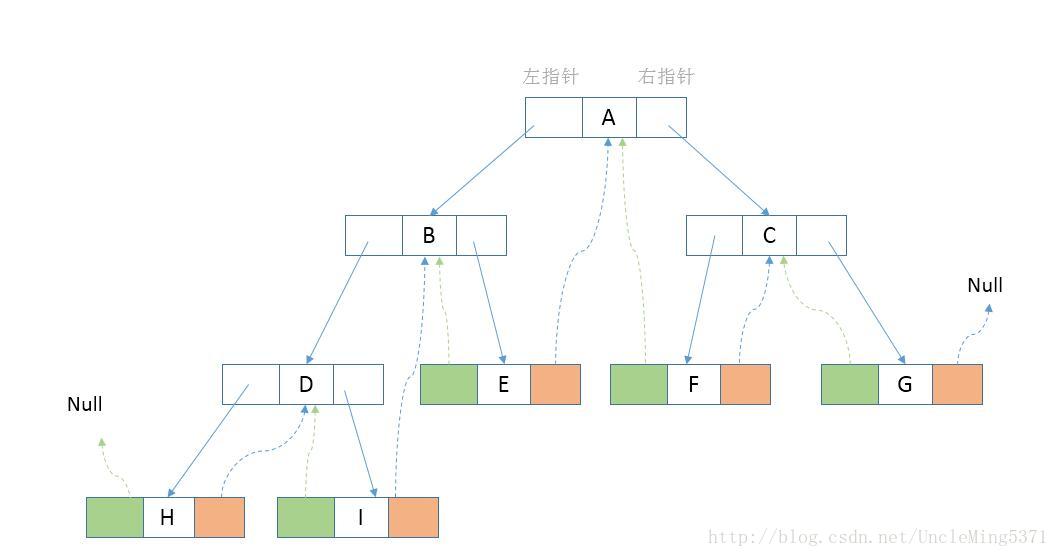
通过观察上图(蓝色虚线代表后继、绿色虚线代表前驱),可以看出,线索二叉树,等于是把一棵二叉树转变成了一个“ 特殊的双向链表“(后面会解释为什么叫特殊的双向链表),这样对于我们的新增、删除、查找节点带来了方便。所以我们对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。如下图:
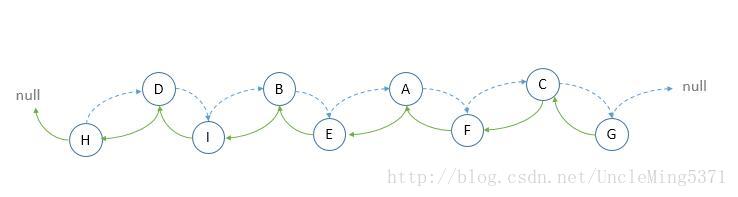
仔细分析上面的双向链表,与线索化之后的二叉树相比,比如节点D与后继节点I,在完成线索化之后,并没有直接线索指针,而是存在父子节点的指针;节点A与节点F,在线索化完成之后,节点A并没有直接指向后继节点F的线索指针,而是通过父子节点遍历可以找到最终的节点F,前驱节点也存在同样的问题,正因为很多节点之间不存在直接的线索,所以我将此双向链表称做“ 特殊的双向链表”,再使用过程中根据指针是线索指针还是子节点指针来分别处理,所以在每个节点需要标明当前的左右指针是线索指针还是子节点指针,这就需要修改节点的数据结构。修改后的数据结构如下:
class Node {
String data; //数据域
Node left; //左指针域
Node right; //右指针域
byte leftType; //左指针域类型 0:指向子节点、1:前驱或后继线索
byte rightType; //右指针域类型 0:指向子节点、1:前驱或后继线索
}最终的二叉链表修改为如下图的样子:
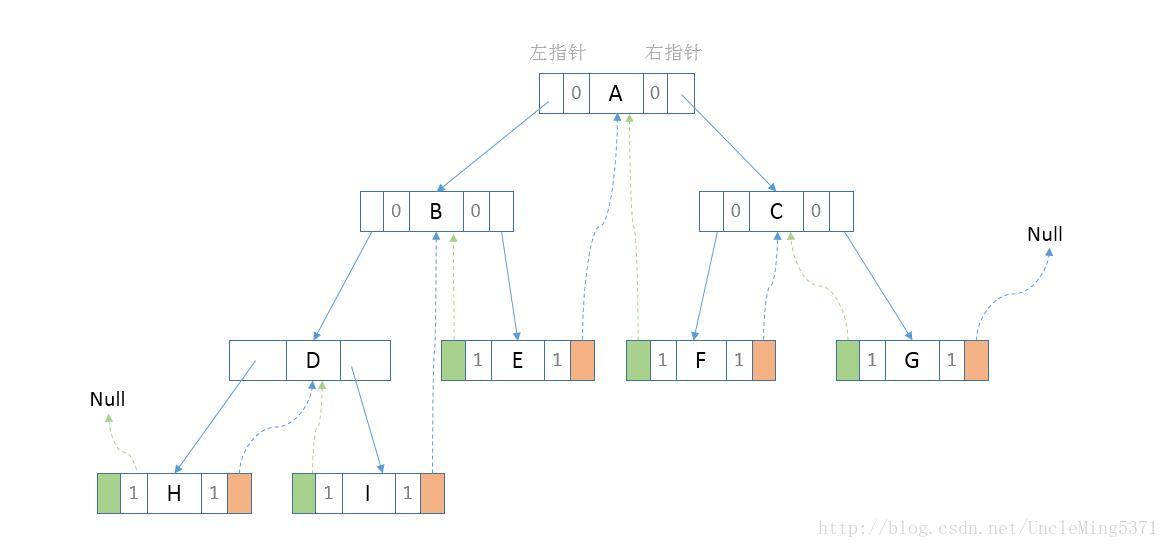
三、线索二叉树的代码(Java版)
下面是中序线索化二叉树的实现代码:
/**
* @Title: 二叉树相关操作
* @Description:
* @Author: Uncle Ming
* @Date:2017年1月6日 下午2:49:14
* @Version V1.0
*/
public class ThreadBinaryTree {
private Node preNode; //线索化时记录前一个节点
//节点存储结构
static class Node {
String data; //数据域
Node left; //左指针域
Node right; //右指针域
boolean isLeftThread = false; //左指针域类型 false:指向子节点、true:前驱或后继线索
boolean isRightThread = false; //右指针域类型 false:指向子节点、true:前驱或后继线索
Node(String data) {
this.data = data;
}
}
/**
* 通过数组构造一个二叉树(完全二叉树)
* @param array
* @param index
* @return
*/
static Node createBinaryTree(String[] array, int index) {
Node node = null;
if(index < array.length) {
node = new Node(array[index]);
node.left = createBinaryTree(array, index * 2 + 1);
node.right = createBinaryTree(array, index * 2 + 2);
}
return node;
}
/**
* 中序线索化二叉树
* @param node 节点
*/
void inThreadOrder(Node node) {
if(node == null) {
return;
}
//处理左子树
inThreadOrder(node.left);
//左指针为空,将左指针指向前驱节点
if(node.left == null) {
node.left = preNode;
node.isLeftThread = true;
}
//前一个节点的后继节点指向当前节点
if(preNode != null && preNode.right == null) {
preNode.right = node;
preNode.isRightThread = true;
}
preNode = node;
//处理右子树
inThreadOrder(node.right);
}
/**
* 中序遍历线索二叉树,按照后继方式遍历(思路:找到最左子节点开始)
* @param node
*/
void inThreadList(Node node) {
//1、找中序遍历方式开始的节点
while(node != null && !node.isLeftThread) {
node = node.left;
}
while(node != null) {
System.out.print(node.data + ", ");
//如果右指针是线索
if(node.isRightThread) {
node = node.right;
} else { //如果右指针不是线索,找到右子树开始的节点
node = node.right;
while(node != null && !node.isLeftThread) {
node = node.left;
}
}
}
}
/**
* 中序遍历线索二叉树,按照前驱方式遍历(思路:找到最右子节点开始倒序遍历)
* @param node
*/
void inPreThreadList(Node node) {
//1、找最后一个节点
while(node.right != null && !node.isRightThread) {
node = node.right;
}
while(node != null) {
System.out.print(node.data + ", ");
//如果左指针是线索
if(node.isLeftThread) {
node = node.left;
} else { //如果左指针不是线索,找到左子树开始的节点
node = node.left;
while(node.right != null && !node.isRightThread) {
node = node.right;
}
}
}
}
/**
* 前序线索化二叉树
* @param node
*/
void preThreadOrder(Node node) {
if(node == null) {
return;
}
//左指针为空,将左指针指向前驱节点
if(node.left == null) {
node.left = preNode;
node.isLeftThread = true;
}
//前一个节点的后继节点指向当前节点
if(preNode != null && preNode.right == null) {
preNode.right = node;
preNode.isRightThread = true;
}
preNode = node;
//处理左子树
if(!node.isLeftThread) {
preThreadOrder(node.left);
}
//处理右子树
if(!node.isRightThread) {
preThreadOrder(node.right);
}
}
/**
* 前序遍历线索二叉树(按照后继线索遍历)
* @param node
*/
void preThreadList(Node node) {
while(node != null) {
while(!node.isLeftThread) {
System.out.print(node.data + ", ");
node = node.left;
}
System.out.print(node.data + ", ");
node = node.right;
}
}
public static void main(String[] args) {
String[] array = {"A", "B", "C", "D", "E", "F", "G", "H"};
Node root = createBinaryTree(array, 0);
ThreadBinaryTree tree = new ThreadBinaryTree();
tree.inThreadOrder(root);
System.out.println("中序按后继节点遍历线索二叉树结果:");
tree.inThreadList(root);
System.out.println("\n中序按后继节点遍历线索二叉树结果:");
tree.inPreThreadList(root);
Node root2 = createBinaryTree(array, 0);
ThreadBinaryTree tree2 = new ThreadBinaryTree();
tree2.preThreadOrder(root2);
tree2.preNode = null;
System.out.println("\n前序按后继节点遍历线索二叉树结果:");
tree.preThreadList(root2);
}
}
四、小结
- 线索化的实质就是将二叉链表中的空指针改为指向前驱节点或后继节点的线索;
- 线索化的过程就是修改二叉链表中空指针的过程,可以按照前序、中序、后序的方式进行遍历,分别生成不同的线索二叉树;
- 有了线索二叉树之后,我们再次遍历时,就相当于操作一个双向链表。
- 使用场景:如果我们在使用二叉树过程中经常需要遍历二叉树或者查找节点的前驱节点和后继节点,可以考虑采用线索二叉树存储结构。
PS: 未完待续…
线索二叉树的原理、前序和中序线索化本文已经尽可能做了详细的描述,对于后序线索化二叉树比较相对复杂,为了避免引起不适,用单独的文章进行了分析,需要的同学请转向后序线索化二叉树。