4. 取样
4.1. 取样
-
取样 (采样)
-
定义:
-
取样 是利用取样脉冲序列 s ( t ) s(t) s(t) 从连续信号 f ( t ) f(t) f(t)中“抽取”一系列离散样本值的过程;得到的离散信号称为取样信号。
-
取样过程可看成由原信号 f ( t ) f(t) f(t) 和取样信号 s ( t ) s(t) s(t) 的乘积来描述。
f S ( t ) = f ( t ) s ( t ) f_S(t) = f(t) s(t) fS(t)=f(t)s(t)- T S T_S TS 取样间隔
- f S = 1 / T S f_S = 1/T_S fS=1/TS 取样频率
- F S ( j ω ) = 1 2 π F ( j ω ) ⋆ S ( j ω ) F_S(j\omega) = \frac{1}{2\pi} F(j\omega) \star S(j\omega) FS(jω)=2π1F(jω)⋆S(jω) 取样信号频谱
-
设 f ( t ) f(t) f(t) 是带限信号, 即 f ( t ) f(t) f(t) 的频谱只在区间 ( − ω m , ω m ) (-\omega_m, \omega_m) (−ωm,ωm) 为有限值,其余区间为 0 0 0 。
f ( t ) ⟷ F ( j ω ) f(t) \longleftrightarrow F(j\omega) f(t)⟷F(jω) -
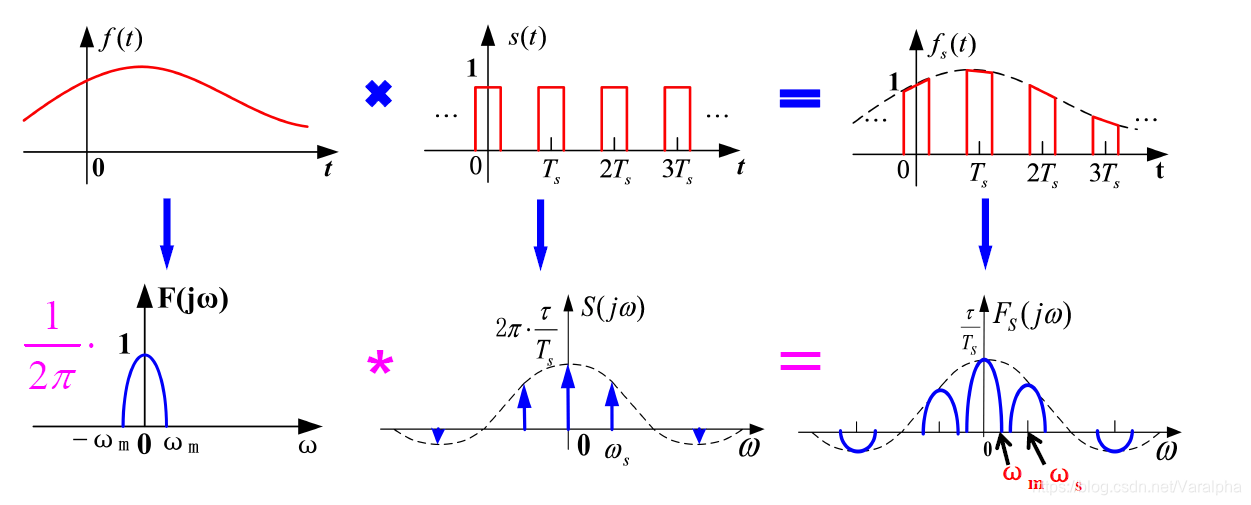
矩形脉冲取样: s ( t ) s(t) s(t) 是周期为 T S T_S TS 的矩形脉冲信号(或称为开关函数) 。
S ( j ω ) = 2 π ∑ n = − ∞ ∞ τ T S Sa ( n ω S τ 2 ) δ ( ω − n ω S ) S(j\omega) = 2\pi \displaystyle\sum^\infty_{n=-\infty}\frac{\tau}{T_S} \text{Sa} \Big(\frac{n\omega_S \tau}{2}\Big)\delta(\omega-n\omega_S) S(jω)=2πn=−∞∑∞TSτSa(2nωSτ)δ(ω−nωS)
F S ( j ω ) = 1 2 π F ( j ω ) ⋆ S ( j ω ) = τ T S ∑ n = − ∞ ∞ Sa ( n ω S τ 2 ) F [ j ( ω − n ω S ) ] F_S(j\omega) = \displaystyle \frac{1}{2\pi} F(j\omega)\star S(j\omega) = \frac{\tau}{T_S} \sum^{\infty}_{n=-\infty} \text{Sa}\Big (\frac{n\omega_S\tau}{2}\Big)F\big[j(\omega-n\omega_S)\big] FS(jω)=2π1F(jω)⋆S(jω)=TSτn=−∞∑∞Sa(2nωSτ)F[j(ω−nωS)]
-
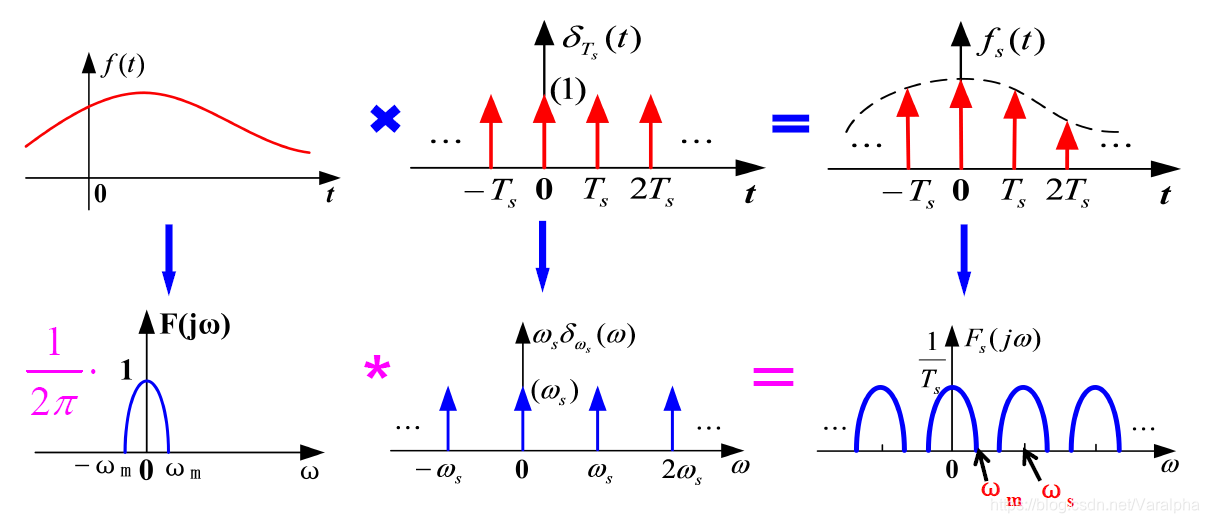
冲激取样: s ( t ) s(t) s(t) 是周期为 T S T_S TS 的冲激函数序列 δ T S ( t ) \delta_{T_S}(t) δTS(t) 。
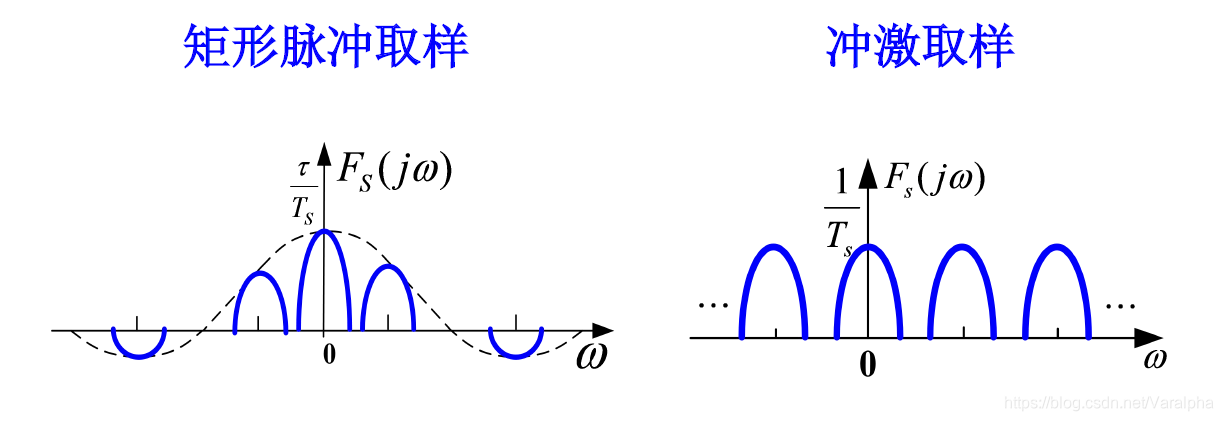
取样 { 自然取样(矩形取样) 理想取样(冲激取样) \begin{aligned} \text{取样} \begin{cases}\text{自然取样(矩形取样)}\\\text{理想取样(冲激取样)} \end{cases} \end{aligned} 取样{自然取样(矩形取样)理想取样(冲激取样)
S ( j ω ) = 2 π ∑ n = − ∞ ∞ 1 T S δ ( ω − n ω S ) S(j\omega) = 2\pi \displaystyle\sum^\infty_{n=-\infty}\frac{1}{T_S} \delta(\omega-n\omega_S) S(jω)=2πn=−∞∑∞TS1δ(ω−nωS)
F S ( j ω ) = 1 2 π F ( j ω ) ⋆ S ( j ω ) = 1 T S ∑ n = − ∞ ∞ F [ j ( ω − n ω S ) ] F_S(j\omega) = \displaystyle \frac{1}{2\pi} F(j\omega)\star S(j\omega) = \frac{1}{T_S} \sum^{\infty}_{n=-\infty} F\big[j(\omega-n\omega_S)\big] FS(jω)=2π1F(jω)⋆S(jω)=TS1n=−∞∑∞F[j(ω−nωS)]
-
Remark:
- 画取样信号
f
S
(
t
)
f_S(t)
fS(t) 的频谱时,设定
ω
S
≥
2
ω
m
\omega_S \geq 2\omega_m
ωS≥2ωm , 此时其频谱不发生混叠,因此利用低通滤波器从
F
S
(
j
ω
)
F_S(j\omega)
FS(jω) 中提取出
F
(
j
ω
)
F(j\omega)
F(jω) , 即从
f
S
(
t
)
f_S(t)
fS(t) 中恢复原信号
f
(
t
)
f(t)
f(t)。否则将发生频谱混叠,而无法恢复原信号。
- 画取样信号
f
S
(
t
)
f_S(t)
fS(t) 的频谱时,设定
ω
S
≥
2
ω
m
\omega_S \geq 2\omega_m
ωS≥2ωm , 此时其频谱不发生混叠,因此利用低通滤波器从
F
S
(
j
ω
)
F_S(j\omega)
FS(jω) 中提取出
F
(
j
ω
)
F(j\omega)
F(jω) , 即从
f
S
(
t
)
f_S(t)
fS(t) 中恢复原信号
f
(
t
)
f(t)
f(t)。否则将发生频谱混叠,而无法恢复原信号。
-
4.1.1. 取样定理 - 时域
-
要点:
- f ( t ) f(t) f(t) 为带限信号 ( − ω m , ω m ) (-\omega_m,\omega_m) (−ωm,ωm) 频谱区间。
- T s ≤ 1 2 f m T_s \leq \frac{1}{2f_m} Ts≤2fm1 均匀采样间隔 f s = 2 f m , T s = 1 / f s f_s = 2f_m,\; T_s = 1/f_s fs=2fm,Ts=1/fs
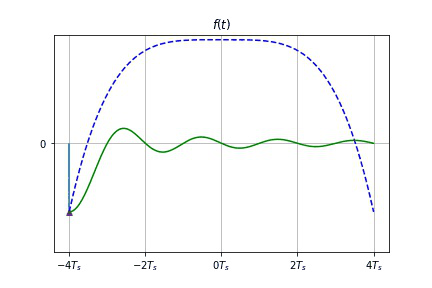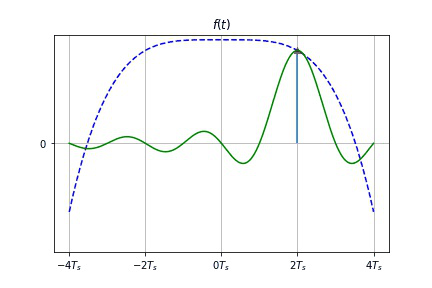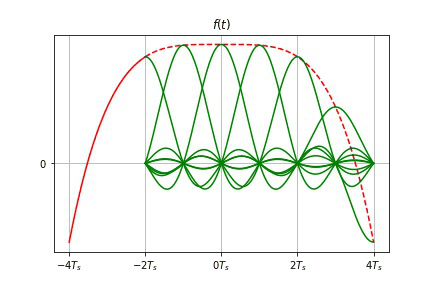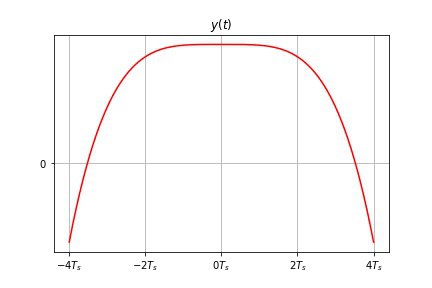
- f ( t ) = ∑ n = − ∞ ∞ f ( n T s ) Sa [ ω s 2 ( t − n T s ) ] f(t) = \sum^{\infty}_{n=-\infty} f(nT_s) \text{Sa} \big[ \frac{\omega_s}{2} (t-nT_s)\big] f(t)=∑n=−∞∞f(nTs)Sa[2ωs(t−nTs)]
-
重要意义:
- 取样定理是连续信号与离散信号间的一座桥梁,为其相互转换提供了理论依据。
- 在一定条件下,一个带限连续信号完全可以用其离散样本值表示。即这些样本值包含了该连续信号的全部信息,用它们可以恢复原信号。
-
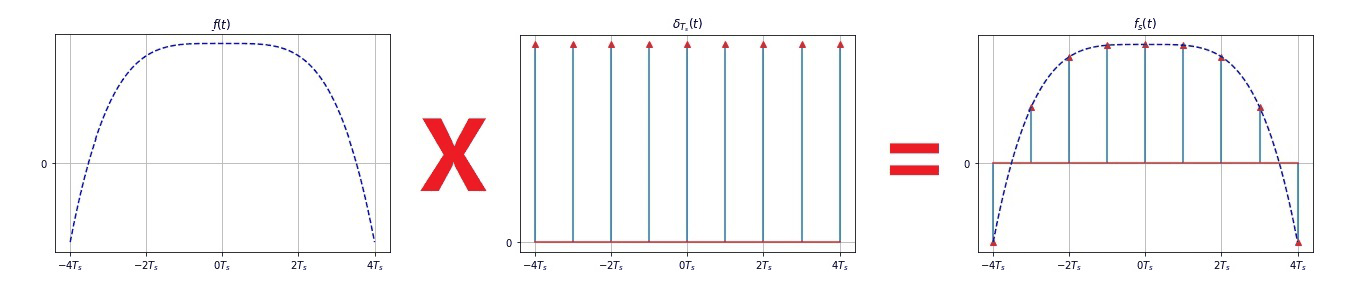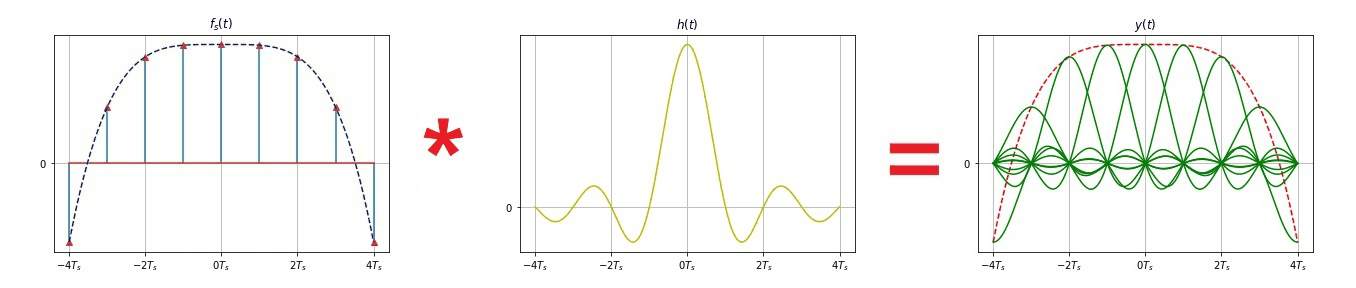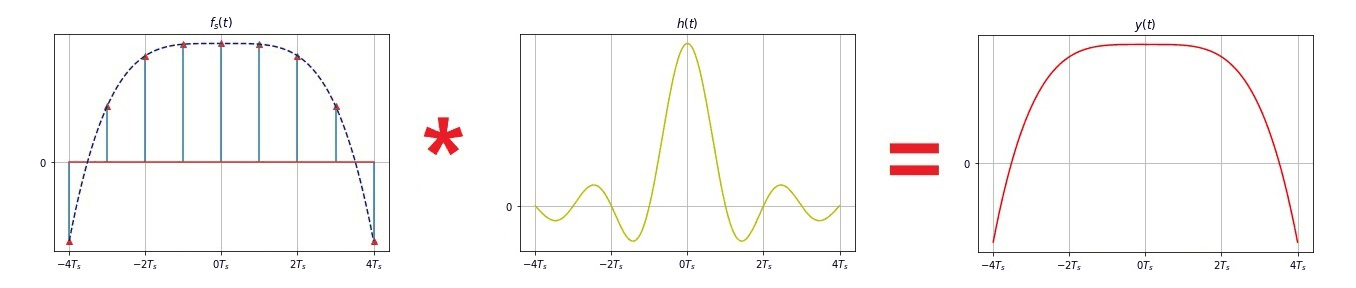
由于
f S ( t ) = f ( t ) s ( t ) = f ( t ) ∑ n = − ∞ ∞ δ ( t − n T S ) = ∑ n = − ∞ ∞ f ( n T S ) δ ( t − n T S ) f_S(t) = f(t) s(t) = f(t) \sum^{\infty}_{n=-\infty} \delta(t-nT_S) = \sum^{\infty}_{n=-\infty} f(nT_S) \delta(t-nT_S) fS(t)=f(t)s(t)=f(t)n=−∞∑∞δ(t−nTS)=n=−∞∑∞f(nTS)δ(t−nTS)- 当
ω
S
≥
2
ω
m
\omega_S \geq 2\omega_m
ωS≥2ωm 时,将冲激取样信号通过低通滤波器:
h ( t ) = T s ω C π Sa ( ω C t ) ⟷ H ( j ω ) = { T S , ∣ ω ∣ < ω C 0 , ∣ ω ∣ > ω C \begin{aligned}\displaystyle h(t) = T_s \frac{\omega_C}{\pi} \text{Sa} (\omega_C t) \longleftrightarrow H(j\omega) = \begin{cases}T_S,\; & \lvert \omega\rvert < \omega_C \\ 0,\; &\lvert \omega\rvert > \omega_C \end{cases} \end{aligned} h(t)=TsπωCSa(ωCt)⟷H(jω)={TS,0,∣ω∣<ωC∣ω∣>ωC - 其截止角频率 ω C \omega_C ωC 取 ω m < ω C < ω S − ω m \omega_m < \omega_C < \omega_S -\omega_m ωm<ωC<ωS−ωm, 即可恢复原信号。
- 为方便, 取 ω C = 0.5 ω S \omega_C = 0.5\omega_S ωC=0.5ωS 。
- 当
ω
S
≥
2
ω
m
\omega_S \geq 2\omega_m
ωS≥2ωm 时,将冲激取样信号通过低通滤波器:
-
取样定理:
f ( t ) = [ ∑ n = − ∞ ∞ f ( n T S ) δ ( t − n T S ) ] ⋆ Sa ( ω S t 2 ) = ∑ n = − ∞ ∞ f ( n T S ) Sa [ ω S 2 ( t − n T S ) ] \begin{aligned}f(t) &= \Big[\sum^{\infty}_{n=-\infty} f(nT_S) \delta(t-nT_S)\Big]\star \text{Sa} (\frac{\omega_S t}{2} ) \\ & = \sum^{\infty}_{n=-\infty} f(nT_S) \text{Sa} \big[\frac{\omega_S}{2} (t-nT_S)\big]\end{aligned} f(t)=[n=−∞∑∞f(nTS)δ(t−nTS)]⋆Sa(2ωSt)=n=−∞∑∞f(nTS)Sa[2ωS(t−nTS)]- 只要已知各取样值
f
(
n
T
s
)
f(nT_s)
f(nTs), 就可唯一地确定出原信号
f
(
t
)
f(t)
f(t)。
- 只要已知各取样值
f
(
n
T
s
)
f(nT_s)
f(nTs), 就可唯一地确定出原信号
f
(
t
)
f(t)
f(t)。
-
时域取样定理:一个频谱在区间 ( − ω m , ω m ) (-\omega_m,\omega_m) (−ωm,ωm) 以外为 0 0 0 的带限信号 f ( t ) f(t) f(t) ,可唯一地由其在均匀间隔 T S [ T S < 1 / ( 2 f m ) ] T_S[T_S<1/(2f_m)] TS[TS<1/(2fm)] 上的样值点 f ( n T S ) f(nT_S) f(nTS) 确定。
-
Remark: 为恢复原信号,必须满足两个条件:
- f ( t ) f(t) f(t) 必须是带限信号;
- 取样频率不能太低,必须 f S > 2 f m f_S>2f_m fS>2fm ,或者说,取样间隔不能太大,必须 T S < 1 / ( 2 f m ) T_S <1/(2f_m) TS<1/(2fm);否则将发生混叠。
-
通常把最低允许的取样频率 f S = 2 f m f_S=2f_m fS=2fm 称为奈奎斯特频率 (Nyquist Sampling Rate),把最大允许的取样间隔 T S = 1 / ( 2 f m ) T_S=1/(2f_m) TS=1/(2fm) 称为奈奎斯特间隔(Nyquist Space) 。
| 信号表达式 | 频谱 | 最高角频率 ω m \omega_m ωm | 奈奎斯特角频率 ω s = 2 ω m \omega_s = 2\omega_m ωs=2ωm |
|---|---|---|---|
| f 1 ( α t ) ; α ≠ 0 f_1(\alpha t);\; \alpha\neq 0 f1(αt);α=0 | 1 ∣ α ∣ F 1 ( j ω α ) \displaystyle\frac{1}{\lvert\alpha\rvert}F_1(j\frac{\omega}{\alpha}) ∣α∣1F1(jαω) | ∣ α ∣ ω m 1 \lvert\alpha\rvert\omega_{m1} ∣α∣ωm1 | 2 ∣ α ∣ ω m 1 2\lvert\alpha\rvert\omega_{m1} 2∣α∣ωm1 |
| f 1 ( t ) + f 2 ( t ) f_1(t) + f_2(t) f1(t)+f2(t) | F 1 ( j ω ) + F 2 ( j ω ) F_1(j\omega)+F_2(j\omega) F1(jω)+F2(jω) | max { ω m 1 , ω m 2 } \max\{\omega_{m1},\omega_{m2}\} max{ωm1,ωm2} | 2 max { ω m 1 , ω m 2 } 2 \max\{\omega_{m1},\omega_{m2}\} 2max{ωm1,ωm2} |
| f 1 ( t ) ⋆ f 2 ( t ) f_1(t) \star f_2(t) f1(t)⋆f2(t) | F 1 ( j ω ) ⋅ F 2 ( j ω ) F_1(j\omega)\cdot F_2(j\omega) F1(jω)⋅F2(jω) | min { ω m 1 , ω m 2 } \min\{\omega_{m1},\omega_{m2}\} min{ωm1,ωm2} | 2 min { ω m 1 , ω m 2 } 2 \min\{\omega_{m1},\omega_{m2}\} 2min{ωm1,ωm2} |
| f 1 ( t ) ⋅ f 2 ( t ) f_1(t) \cdot f_2(t) f1(t)⋅f2(t) | 1 2 π F 1 ( j ω ) ⋆ F 2 ( j ω ) \frac{1}{2\pi}F_1(j\omega)\star F_2(j\omega) 2π1F1(jω)⋆F2(jω) | ω m 1 + ω m 2 \omega_{m1}+\omega_{m2} ωm1+ωm2 | 2 ( ω m 1 + ω m 2 ) 2 (\omega_{m1}+\omega_{m2}) 2(ωm1+ωm2) |
| f 1 2 ( t ) f_1^2(t) f12(t) | 1 2 π F 1 ( j ω ) ⋆ F 1 ( j ω ) \frac{1}{2\pi}F_1(j\omega)\star F_1(j\omega) 2π1F1(jω)⋆F1(jω) | 2 ω m 1 2\omega_{m1} 2ωm1 | 4 ω m 1 4\omega_{m1} 4ωm1 |
4.1.2. 取样定理 - 频域
-
根据时域与频域的对偶性,可推出频域取样定理
-
一个在时域区间 ( − t m , t m ) (-t_m,t_m) (−tm,tm) 以外为 0 0 0 的 时限信号 f ( t ) {\color{blue}\text{时限信号}f(t)} 时限信号f(t) 的频谱函数 F ( j ω ) F(j\omega) F(jω) ,可唯一地由其在均匀频率间隔 f s [ f s < 1 / ( 2 t m ) ] f_s[{\color{blue}f_s<1/(2t_m)}] fs[fs<1/(2tm)] 上的样值点 F ( j n ω s ) F(jn\omega_s) F(jnωs) 确定。
F ( j ω ) = ∑ n = − ∞ ∞ F ( j n π t m ) Sa ( ω t m − n π ) , t m = 1 2 f s F(j\omega) =\displaystyle \sum^{\infty}_{n=-\infty} F(j\frac{n\pi}{t_m}) \text{Sa} (\omega t_m -n\pi), \; t_m = \frac{1}{2f_s} F(jω)=n=−∞∑∞F(jtmnπ)Sa(ωtm−nπ),tm=2fs1
4.1.3. Python 实现Sa信号的采样和恢复
- 信号 S a ( t ) Sa(t) Sa(t) 作为被采样信号,信号带宽 B = 1 B=1 B=1 , 采样频率 ω s = 2 B \omega_s=2B ωs=2B ,此频率下的采样为 Nyquist 采样,对采样及恢复过程用 Python 进行仿真。
# 导入 需要的 library 库
import numpy as np # 科学计算
import matplotlib.pyplot as plt # 画图工具
import scipy.signal as sg # 导入 scipy 的 signal 库 重命名为 sg
# 用 Python 表示
B = 1 # 信号带宽
wc = B # 滤波器截止频率
Ts = np.pi/B # 采样间隔
ws = 2*np.pi/Ts # 采样角频率
N = 100 # 滤波器时域采样点数
n = np.arange(-N,N+1)
nTs = n *Ts # 采样数据的采样时间
fs = np.sinc(nTs/np.pi) # 函数的采样点
Dt = 0.005 # 恢复信号的采样间隔
t = np.arange(-15,15+Dt,Dt) # 恢复信号的范围
fa = np.dot(fs,Ts*wc/np.pi*np.sinc((wc/np.pi)*np.ones((len(nTs),1))*t -nTs.reshape(1,201).T*np.ones((1,len(t))))) # 信号重构
error = np.abs(fa-np.sinc(t/np.pi)) # 求重构信号与原信号的归一化误差
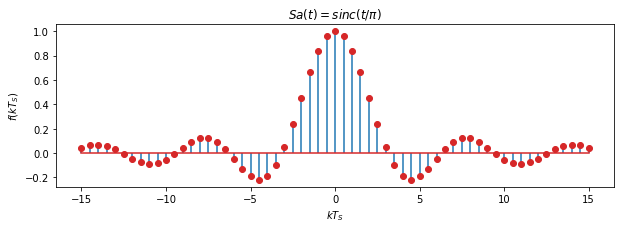
# Nyquist 抽样信号
plt.figure(figsize=(10,3))
plt.stem(t[::100], np.sinc(t/np.pi)[::100], '-',label='f1', markerfmt='C3o', use_line_collection=True)
plt.ylabel(r'$f(kT_S)$')
plt.xlabel(r'$kT_S$')
plt.title(r'$Sa(t) = sinc(t/\pi)$')
plt.show()
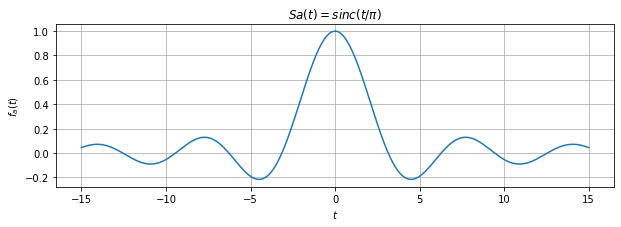
# Nyquist抽样信号重构sa(t)
plt.figure(figsize=(10,3))
plt.plot(t,fa)
plt.grid(True)
plt.ylabel(r'$f_a(t)$')
plt.xlabel(r'$t$')
plt.title(r'$Sa(t) = sinc(t/\pi)$')
plt.show()
# Nyquist抽样信号与原信号的误差error(t)
plt.figure(figsize=(10,3))
plt.plot(t,error)
plt.grid(True)
plt.ylabel(r'$error(t)$')
plt.xlabel(r'$t$')
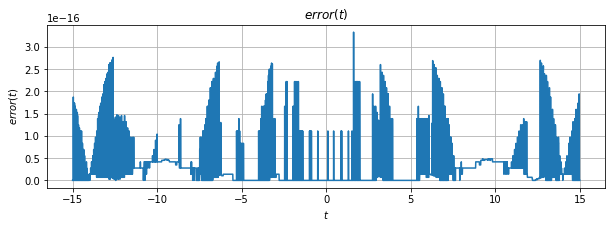
plt.title(r'$error(t)$')
plt.show()
- 从误差图形中可以看到,用采样信号恢复的信号与原始信号的误差是极小的,而且这种误差来自于计算过程的数值计算误差。
- 表明:对一个信号进行Nyquist采样后,能够无误差地从采样信号中恢复出原信号。
4.1.4. 应用案例: CD数字录音系统
-
CD数字录音系统:
- 麦克风采集声音信号,并输出模拟电信号,即麦克风实现 声电转换 的功能;
- 模拟低通滤波器对来自麦克风的模拟信号进行 滤波 ,滤除高频噪声;
- 为了便于后续的数字处理,需要对模拟信号进行 采样保持 ;
- 将模拟信号进行采样以后得到的信号一般称为 离散信号 。离散信号需要进行 模数转换 (Analog Digital Convert, ADC),得到 数字信号 ,这个过程称为 量化 ;
- 将数字信号编码、调制、同步处理后刻入CD。
-
关键问题:
- CD系统如何选择采样率?
- CD系统的设计目标是期望能够记录下人类听觉系统所能听到的所有声音,其频率范围是 20Hz ~ 20KHz;由时域采样定理知道,采样频率要达到原始信号的 2 倍。这就是图中采样率是 44.1KHz 的原因,采用 44.1KHz 而不是 40KHz 是为了留有一定余量。当然,采样频率越大越有利于完美再现原始信号,但过高的采样率将导致数据量过大。