1 XGBoost原理阐述

1.1 关于决策树与集成模型

  将决策树与集成学习框架进行结合的常用模型包括：

1. $Bagging$ + 决策树 = 随机森林($RandomForest$)
2. $AdaBoost$ + 决策树 = 提升树($BoostingDecisionTree$)
3. $GradientBoosting$ + 决策树 = 梯度提升树($GradientBoostingDecisionTree$)

  其中 XGBoost 就是梯度提升树(GBDT)的实现库，所以在搞清楚 XGBoost 之前需要先理解 GBDT。

1.2 梯度提升树

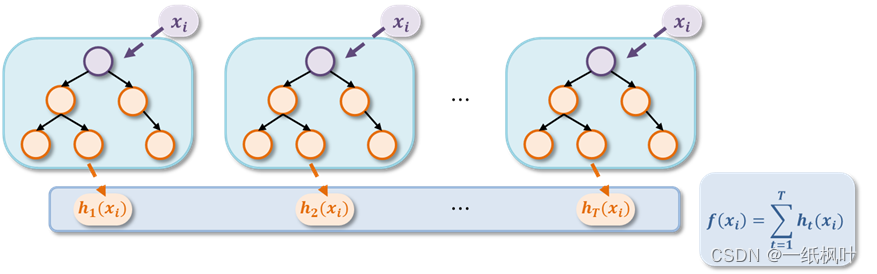
  GBDT 又叫 MART(Multiple Additive Regression Tree)，是一种基于$Boosting$ 的集成思想的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终的答案，GBDT 集成模型简要示意图如下所示：

1.2.1 回归决策树(regression Decision Tree)

  对比分类决策树与回归决策树：

• 分类 DT：通过 最大化熵 的思想划分属性分支，叶子节点的值是类别。
• 回归 DT：通过 最小化均方差 的思想，且每个节点的值都是预测值而非类别。

1.2.2 梯度迭代(Gradient Boosting)

  GB 的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。
  例如取预测值与真实值的误差作为下一棵树的输入，此时梯度迭代的示意图如下所示：

  在此基础上，引入损失函数，将损失函数的值作为每一轮次决策树估计结果的残差，此时梯度迭代的示意图如下所示：

1.2.3 梯度提升树(GBDT)的迭代目标

  GBDT 的每一轮迭代目标：找到一个 CART 回归树模型的弱学习器 $h_t(x)$，让本轮的损失函数 $L\left(y,f_t(x)\right)=L\left(y,f_{t-1}(x)+h_t(x)\right)$ 最小。

1.2.4 如何拟合损失函数

  在文献中，$Frideman$ 提出了利用损失函数的负梯度值来近似拟合本轮损失函数值，进而拟合一个 CART 回归树。设第 $t$ 轮中样本 $x_i$ 的损失函数负梯度表达式为：
$$r_{ti}=-{\left[\frac{\partial L(y_i,f\left({\mathbf{x}}_i\right)}{\partial f\left({\mathbf{x}}_i\right)}\right]}_{f(\mathbf{x})=f_{t-1}(\mathbf{x})}\text{\hspace{1em}(1)}$$

  其中 $f(\mathbf{x})$ 取上一轮生成的强学习器 $f_{t-1}(\mathbf{x})$。在此基础上，利用所有样本的损失函数负梯度 $\left({\mathbf{x}}_i,r_{ti}\right),(i=1,2,\cdots ,m)$ 可以拟合出整个CART回归树：

  使用损失函数的负梯度值作为 CART 回归树的输入，此时单棵 CART 回归树的生成步骤如下所示：
  每一轮树的生成需要明确两个关键点：

• 从备选的属性集合中选择一个属性 $A$
• 在该属性中找出一个最佳划分点 $s$

对应的生成原则为：要使得划分后两个集合 ${\mathbf{D}}_1$ 和${\mathbf{D}}_2$ 中样本的样本均方误差和最小 & 两个集合的均方误差和最小，即：

$$\underset{\mathbf{A},\mathbf{s}}{\min }\left\{\underset{{\mathbf{D}}_1}{\min }\sum _{{\mathbf{x}}_{\mathbf{i}}\in {\mathbf{D}}_1(\mathbf{A},\mathbf{s})}{\left(r_{ti}-c_{t1}\right)}^2+\underset{D_2}{\min }\sum _{x_i\in D_2(A,s)}{\left(r_{ti}-r_{t2}\right)}^2\right\}\text{\hspace{1em}(2)}$$

  其中 $c_{t1}$ ，$c_{t2}$ 是经过 $(A,s)$ 划分之后两块区域的输出值 / 叶子节点值。按照该原则划分会将训练集中的样本划分成两个区域：$R_{t1}(A,s)=\left\{x\mid x^{(A)}\le s\right\}$ 和 $R_{t2}(A,s)=\left\{x\mid x^{(A)}>s\right\}$，而 $c_{t1}$ , $c_{t2}$ 计算表达式为：

$$c_{t1}=\frac{1}{R_1\text{ 中样本个数 }}\sum _{x_i\in R_{t1}(A,s)}{r}_{ti}\text{\hspace{1em}(3)}$$
$$c_{t2}=\frac{1}{R_2\text{ 中样本个数 }}\sum _{x_i\in R_{t2}(A,s)}{r}_{ti}\text{\hspace{1em}(4)}$$

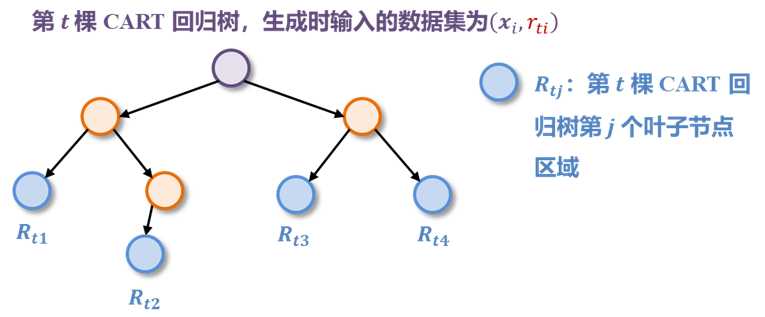
  通过上述方式，逐步对回归树进行分裂，到最终会得到一共 $J$ 个划分区域 / 叶子节点 $R_{tj}$ ，每个区域都会被分到若干个训练集样本 $\left({\mathbf{x}}_i,r_{ti}\right)$ ，而每个叶子节点的输出值就是落在这些节点上的所有样本的标签值的均值：

$$c_{tj}=\frac{1}{Nu{m}_{R_{tj}}}\sum _{x_i\in R_{tj}}{r}_{ti}\text{\hspace{1em}(5)}$$

  当所有区域的输出值都求出来后，这一棵 CART 回归树也就构建完成了。对于一个未知样本 $x$ 而言，该 CART 回归树的预测结果为：

$$h_t(\mathbf{x})=\sum _{j=1}^J\left[c_{tj}\cdot I\left(x\in R_{tj}\right)\right]\text{\hspace{1em}(6)}$$

  其中 $I\left(x\in R_{tj}\right)$ 是指标函数，即只有 $\mathbf{x}$ 样本被划分到的那个对应区域 $R_{tj}$ 中$I\left(x\in R_{tj}\right)=1$，其余清空下$I\left(x\in R_{tj}\right)=0$

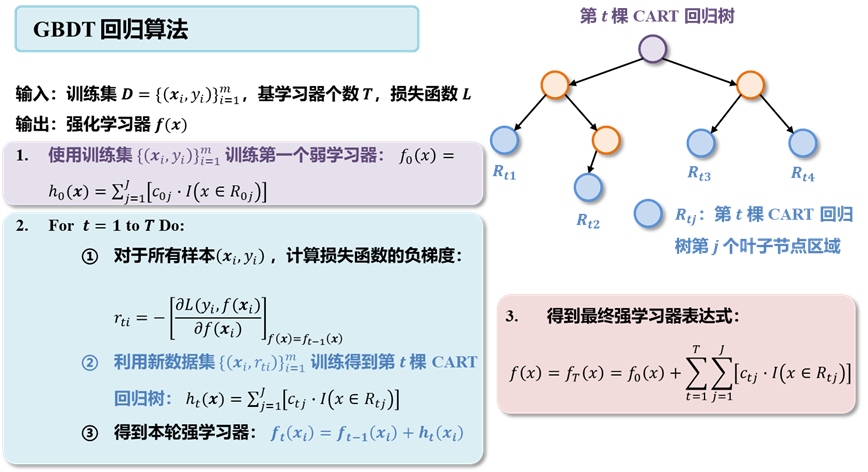
1.2.5 GBDT回归算法思路

  综合以上，GBDT 的算法设计思路如下所示：

1.3 XGBoost 原理

  XGBoost(Extreme Gradient Boosting regression Decision Tree)是 GBDT 模型的一种高效的改进实现算法，其设计思想主要在于改进 GBDT中单颗 CART 回归树的生成步骤。
  在 CART 回归树的生成步骤中，有两步比较关键：

• 对输入数据集做若干次划分，得到若干个最优划分区域/叶子节点 $R_{tj}$
• 计算出各个区域 / 叶子节点的输出值 $c_{tj}$

  在 GBDT 模型中，上述两个步骤是分开逐个求解的，而在 XGBoost 中，上述两个步骤将会合并求解，即一步同时求出划分区域以及区域最佳输出值，同时优化了 GBDT 的损失函数。上述两个步骤将会合并求解，即一步同时求出划分区域以及区域最佳输出值，同时优化了 GBDT 的损失函数。

1.3.1 XGBoost 损失函数设计

  GBDT 的损失函数为(第 $t$ 轮迭代时)：
$$L_t=L\left(y,f_t\left({\mathbf{x}}_i\right)\right)=L\left(y,f_{t-1}\left({\mathbf{x}}_i\right)+h_t\left({\mathbf{x}}_i\right)\right)=L\left(y,\sum _{t=1}^{t-1}{h}_t\left({\mathbf{x}}_i\right)\right)\text{\hspace{1em}(7)}$$
  在此基础上，加入正则化项：
$$\Omega \left(h_t\right)=\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2\text{\hspace{1em}(8)}$$
  其中 ${\omega }_{tj}^2$ 为第 $t$ 棵回归树中第 $j$ 个叶子节点的输出值(和前面 $c_{tj}^2$ 一致→ 为了和原论文保持一致换的)，$J$ 是 CART 树中叶子节点数，而 $\gamma$ 和 $\lambda$ 是正则化系数。
  加入正则化项之后的损失函数为：
$$L_t=\underset{L\left(y,f_{t-1}\left({\mathbf{x}}_i\right)+h_t\left({\mathbf{x}}_i\right)\right)}{\underbrace{\sum _{i=1}^{m}L\left(y,\sum _{t=1}^{t-1}{h}_t\left({\mathbf{x}}_i\right)\right)}}+\underset{\Omega \left(h_t\right)}{\underbrace{\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2}}\text{\hspace{1em}(9)}$$
  该函数也是 XGBoost 要最小化的单回归树损失函数。通过求解上述函数的最小值，得到第 $t$ 个决策树最优的所有 $J$ 个叶子节点区域 { R t j ∣ 1 ≤ j ≤ J } \left\{R_{t j} \mid 1 \leq j \leq J\right\} {Rtj​∣1≤j≤J} 和每个叶子节点区域的最优解 ${\omega }_{tj}^2$:

argmin ⁡ { R t j ∣ 1 ≤ j ≤ J } , ω t j 2 [ ∑ i = 1 m L ( y , ∑ t = 1 t − 1 h t ( x i ) ) ⏟ L ( y , f t − 1 ( x i ) + h t ( x i ) ) + γ J + λ 2 ∑ j = 1 J ω t j 2 ⏟ Ω ( h t ) ] (10) \underset{\left\{R_{t j} \mid 1 \leq j \leq J\right\}, \quad \omega_{t j}^2}{\operatorname{argmin}}[\underbrace{\sum_{i=1}^m L\left(y, \sum_{t=1}^{t-1} h_t\left(\boldsymbol{x}_i\right)\right)}_{L\left(y, f_{t-1}\left(\boldsymbol{x}_i\right)+h_t\left(\boldsymbol{x}_i\right)\right)}+\underbrace{\gamma J+\frac{\lambda}{2} \sum_{j=1}^J \omega_{t j}^2}_{\Omega\left(h_t\right)}] \tag{10} {Rtj​∣1≤j≤J},ωtj2​argmin​[L(y,ft−1​(xi​)+ht​(xi​)) i=1∑m​L(y,t=1∑t−1​ht​(xi​))​​+Ω(ht​) γJ+2λ​j=1∑J​ωtj2​​​](10)

  对损失函数进行2阶泰勒展开：

$$L_t=\sum _{i=1}^{m}L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)+h_t\left({\mathbf{x}}_i\right)\right)+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2\text{\hspace{1em}(11)}$$
  进一步展开：
$$L_t\approx \sum _{i=1}^{m}L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)+\frac{\partial L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)}{\partial f_{t-1}\left({\mathbf{x}}_i\right)}\cdot h_t\left({\mathbf{x}}_i\right)+\frac{1}{2}\cdot \frac{\partial L_{t-1}^2\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)}{\partial f_{t-1}^2\left({\mathbf{x}}_i\right)}\cdot {\left[h_t\left({\mathbf{x}}_i\right)\right]}^2+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2\text{\hspace{1em}(12)}$$

  为了简化运算，令：
$$g_{ti}=\frac{\partial L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)}{\partial f_{t-1}\left({\mathbf{x}}_i\right)}\text{\hspace{1em}(13)}$$
$$h_{ti}=\frac{\partial L_{t-1}^2\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)}{\partial f_{t-1}^2\left({\mathbf{x}}_i\right)}\text{\hspace{1em}(14)}$$
  此时损失函数的近似表达式为：
$$L_t\approx \sum _{i=1}^m\left[L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)+g_{ti}\cdot h_t\left({\mathbf{x}}_i\right)+\frac{1}{2}\cdot h_{ti}\cdot {\left[h_t\left({\mathbf{x}}_i\right)\right]}^2\right]+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2\text{\hspace{1em}(15)}$$
  在上述的损失函数的泰勒近似中， $L\left(y_i,f_{t-1}\left({\mathbf{x}}_i\right)\right)$ 是固定常数，可以去掉，同时由于每个回归树的第 $j$ 个叶子节点的取值最终会是同一个值 ${\omega }_{tj}$，故抛掉该项后继续化简该式子：

$$L_t\approx \sum _{i=1}^m\left[g_{ti}\cdot h_t\left({\mathbf{x}}_i\right)+\frac{1}{2}\cdot h_{ti}\cdot {\left[h_t\left({\mathbf{x}}_i\right)\right]}^2\right]+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2\text{\hspace{1em}(16)}$$
  其中：
$$\sum _{i=1}^m\left[g_{ti}\cdot h_t\left({\mathbf{x}}_i\right)\right]=\sum _{i=1}^m\left[g_{ti}\cdot \sum _{j=1}^J\left[{\omega }_{tj}\cdot I\left(x\in R_{tj}\right)\right]\right]=\sum _{j=1}^J\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{g}_{ti}\cdot {\omega }_{tj}\right)\text{\hspace{1em}(17)}$$
$$\sum _{i=1}^m\left[h_{ti}\cdot {\left[h_t\left({\mathbf{x}}_i\right)\right]}^2\right]=\sum _{i=1}^m\left\{h_{ti}\cdot {\left[\sum _{j=1}^J\left[{\omega }_{tj}\cdot I\left(x\in R_{tj}\right)\right]\right]}^2\right\}=\sum _{j=1}^J\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{g}_{ti}\cdot {\omega }_{tj}^2\right)\text{\hspace{1em}(18)}$$
  将上述结果代入式子中有：
$$\begin{gathered} L_t\approx \sum _{i=1}^m\left[g_{ti}\cdot h_t\left({\mathbf{x}}_i\right)+\frac{1}{2}\cdot h_{ti}\cdot {\left[h_t\left({\mathbf{x}}_i\right)\right]}^2\right]+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2 \\ \approx \sum _{j=1}^J\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{g}_{ti}\cdot {\omega }_{tj}+\frac{1}{2}\sum _{{\mathbf{x}}_i\in R_{tj}}{h}_{ti}\cdot {\omega }_{tj}^2\right)+\gamma J+\frac{\lambda }{2}\sum _{j=1}^J{\omega }_{tj}^2 \\ \approx \sum _{j=1}^J\left[\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{g}_{ti}\right)\cdot {\omega }_{tj}+\frac{1}{2}\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{h}_{ti}+\lambda \right)\cdot {\omega }_{tj}^2\right]+\gamma J \end{gathered}$$
  为了进一步简化运算，继续对式子中的元素进行换元：
$$\{\begin{array}{rl}{G}_{ti}& =\left(\sum _{x_i\in R_{tj}}{g}_{ti}\right)\\ H_{ti}& =\left(\sum _{{\mathbf{x}}_i\in R_{tj}}{h}_{ti}\right)\end{array}\text{\hspace{1em}(19)}$$

  将换元结果代入损失函数表达式有：
$$L_t\approx \sum _{j=1}^J\left[G_{ti}\cdot {\omega }_{tj}+\frac{1}{2}\left(H_{ti}+\lambda \right)\cdot {\omega }_{tj}^2\right]+\gamma J\text{\hspace{1em}(20)}$$
  该表达式就是 XGBoost 最终构造的损失函数。

1.3.2 XGBoost 目标函数建立与求解

  经过上述推导，XGBoost 的优化目标函数为：
argmin ⁡ { R t j ∣ 1 ≤ j ≤ J } , ω t j 2 [ ∑ j = 1 J [ G t i ⋅ ω t j + 1 2 ( H t i + λ ) ⋅ ω t j 2 ] + γ J ] (21) \underset{\left\{R_{t j} \mid 1 \leq j \leq J\right\}, \quad \omega_{t j}^2}{\operatorname{argmin}}\left[\sum_{j=1}^J\left[G_{t i} \cdot \omega_{t j}+\frac{1}{2}\left(H_{t i}+\lambda\right) \cdot \omega_{t j}^2\right]+\gamma J\right] \tag{21} {Rtj​∣1≤j≤J},ωtj2​argmin​[j=1∑J​[Gti​⋅ωtj​+21​(Hti​+λ)⋅ωtj2​]+γJ](21)
  优化求解目标函数，XGBoost 设计了一种可以同时求出回归树最优的所有 $J$ 个叶子节点区域和每个叶子节点区域的最优解，这个设计可以拆成2个部分：

• 如果已经求出了第 $t$个回归树的 $J$ 个最优的叶子节点区域，如何求出每个叶子节点区域最优解 ${\omega }_{tj}$?
• 对当前回归树做子树分裂决策时，应该如何选择属性 $A$ 和对应的属性值$s$ 进行分裂，使得损失函数 $L_t$ 最小?

问题 1：求解最优 ${\mathbf{\omega }}_{\mathbf{tj}}$

  求解方法：直接在损失函数 $L_t$上对求 ${\omega }_{tj}$ 的偏导数，并取其偏导数为 0 时 ${\omega }_{tj}$ 的值为最优解：
$$\frac{\partial L_t}{\partial {\omega }_{tj}}=0\to {\omega }_{tj}=-\frac{G_{tj}}{H_{tj}+\lambda }\text{\hspace{1em}(22)}$$

问题 2：构建回归树时分裂规则设计 (求解最优 { R t j ∣ 1 ≤ j ≤ J } \left\{\boldsymbol{R}_{\boldsymbol{t} j} \mid \mathbf{1} \leq \boldsymbol{j} \leq \boldsymbol{J}\right\} {Rtj​∣1≤j≤J} )

  在 GBDT 中，使用 CART 回归树，节点属性选择和最佳分裂点选择都是基于均方误差最小的思想设计的，通过这种均方误差最小的分裂方式，间接的降低了每一轮迭代中损失函数的值，最后成功实现损失函数最小的目标。
  在 XGBoost 中则不再单纯使用均方误差最小化的思路来设计回归树，而是使用了贪心法，即每次分裂都期望直接最小化总损失函数 / 目标函数的误差。
  假设 ${\omega }_{tj}$ 的值已经是最优解，将最优解代入到损失函数有：
$$L_t=-\frac{1}{2}\sum _{j=1}^J\left(\frac{G_{tj}^2}{H_{tj}+\lambda }+\gamma J\right)\text{\hspace{1em}(23)}$$
  设计思路：在左右子树分裂时，最大程度减少上面损失函数的损失。
  假设某个数据集节点被某个属性的某个取值标准分成左右子树，且对应的1阶和2阶导数和值为：$G_L$,$H_L$, $G_R$,$H_R$，则对应有：

1. 分裂之前的损失函数值：
   $$L_{Before}=-\frac{1}{2}\cdot \frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }+\gamma J\text{\hspace{1em}(24)}$$
2. 左子树损失函数值：
   $$L_{Left}=-\frac{1}{2}\cdot \frac{G_L^2}{H_L+\lambda }+\gamma J\text{\hspace{1em}(25)}$$
3. 右子树损失函数值：
   $$L_{Right}=-\frac{1}{2}\cdot \frac{G_R^2}{H_R+\lambda }+\gamma J\text{\hspace{1em}(25)}$$

  损失函数的损失最小化即为让树节点分裂后的损失函数和减去分裂前的损失函数和这个差值最小，即：$\mathbf{min}$(分裂后的损失函数和 – 分裂前的损失)
$$\begin{array}{rl}\min \Delta & =\min \left[\left(L_{Left}+L_{\text{Right }}\right)-L_{\text{Before }}\right]\\ & =\min \left\{\left[\left(-\frac{1}{2}\cdot \frac{G_L^2}{H_L+\lambda }+\gamma J\right)+\left(-\frac{1}{2}\cdot \frac{G_R^2}{H_R+\lambda }+\gamma J\right)\right]-\left(-\frac{1}{2}\cdot \frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }+\gamma J\right)\right\}\end{array}\text{\hspace{1em}(26)}$$
  经过化简，将最小化转为最大化：
$$\max \left\{\frac{1}{2}\cdot \left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }-\gamma \right]\right\}\text{\hspace{1em}(27)}$$
  综合以上，在构造一棵回归树时，每一轮在选择 以何种属性($A$) 和 该属性中哪个划分点值($s$) 对回归树进行划分，只需要找到一对$(A,s)$组合，使得下面的表达式值最大即可：
$$\underset{(A,s)}{\mathrm{argmax}}\left\{\frac{1}{2}\cdot \left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }-\gamma \right]\right\}\text{\hspace{1em}(27)}$$

2 XGBoost 算法设计思路

  XGBoost 算法设计思路如下所示：