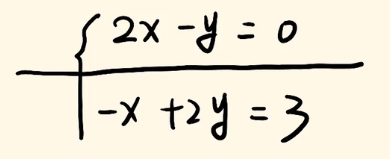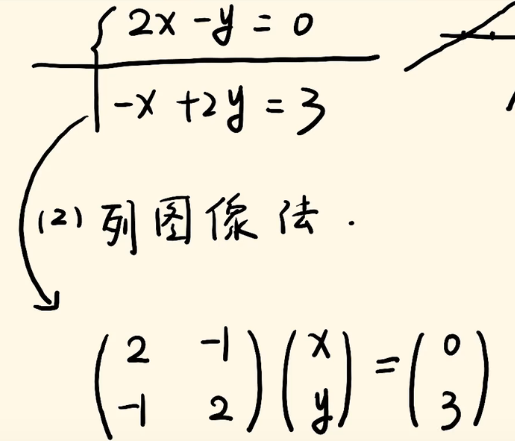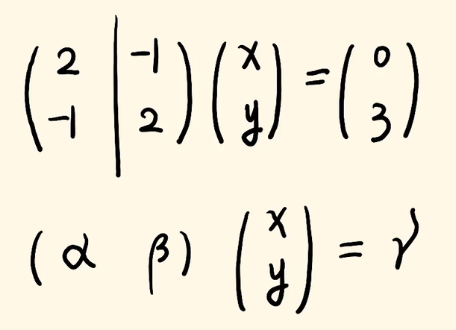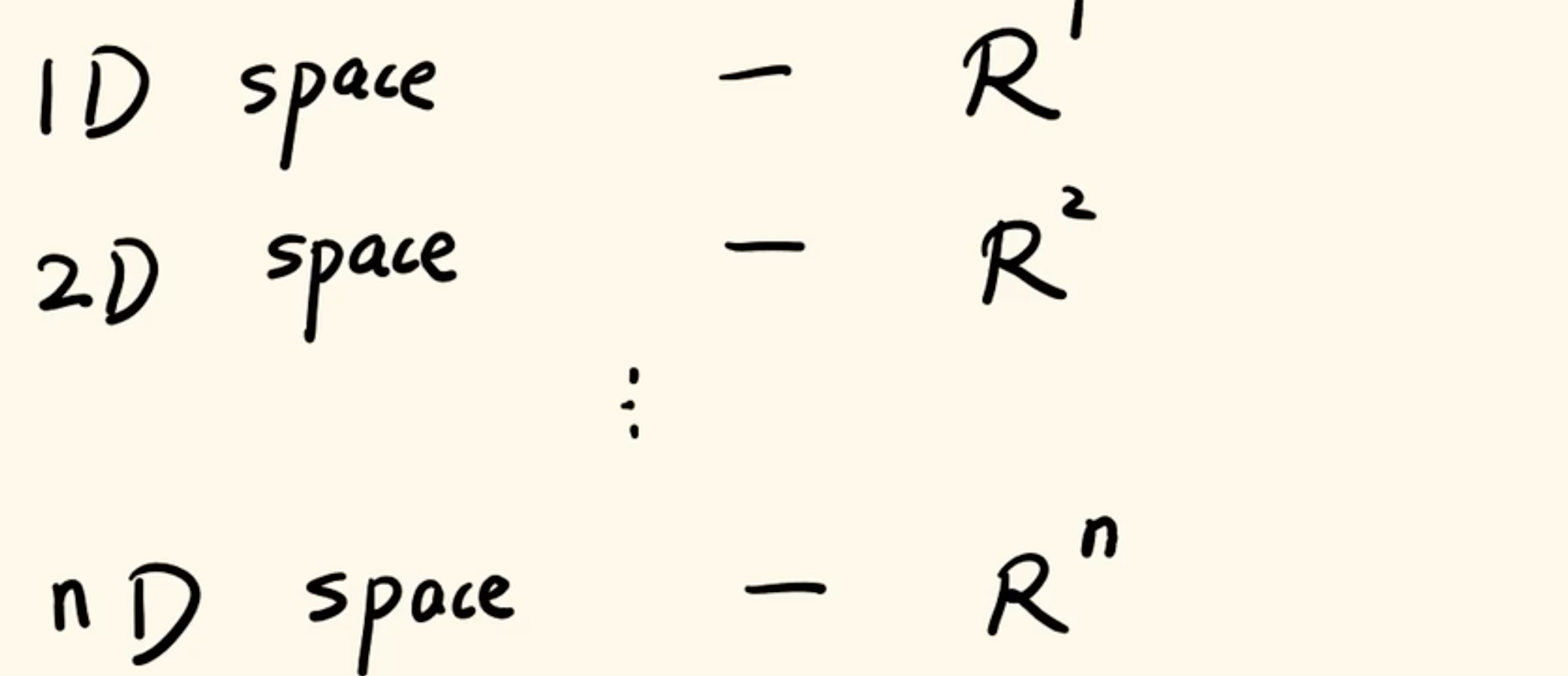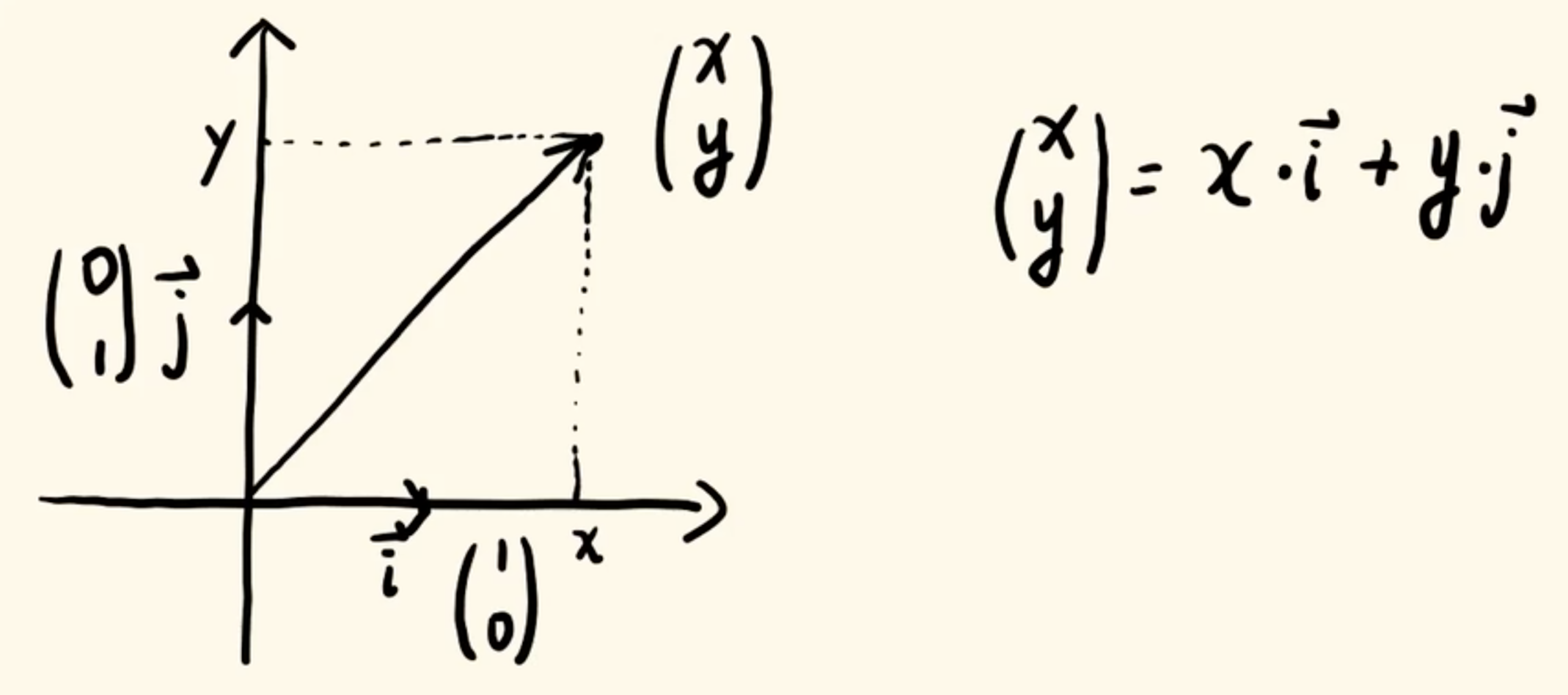视频1:向量及方程组
原视频:线性代数预备知识——向量及方程组_哔哩哔哩_bilibili
很多同学没办法把线性代数的前后章节联系到一起,比如第三章的向量组和第四章的方程组它们之间到底有什么关系?为了解决大家的疑惑,我接下里将会做一系列的视频来帮助大家更好地学习线代。本期视频我们要聊的是一些预备知识。
一、向量/矢量(vector)
1、向量和标量的区别
向量:又叫矢量,英文叫vector。它是与标量相对的一个量。向量是一个有大小、有方向的量。在中学物理我们学过很多类似的量,比如力(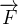
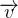
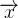
标量:是一个仅有大小的量。这种量有很多,比如温度、体积、面积等
2、向量的坐标
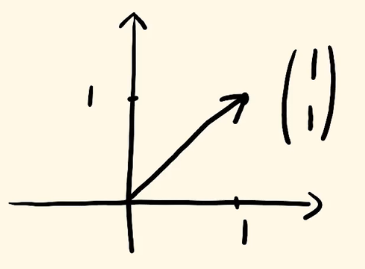
向量的坐标和点的坐标是一致的。因为在线性代数中,我们在研究向量的时候,其实我们就是在研究这个向量所对应的点。因为我们在研究这个点的时候我们不把它看作点,而是看做由原点出发,到这个点的一个向量。👇
注意:我们在线性代数中,我们总是把向量写作列向量,或者说总是以列的形式来描述一个向量的坐标。
总结:向量是一个有大小、有方向的量,它是一个有向线段,
二、线性方程组(Linear Equations)
我们来看第二个预备知识——线性方程组
上图👆的方程组用我们很容易就能解出来(初中的消元法)
下面我们来看一下它的几何解法,即在图像上这个方程组是个什么情况👇
1、行图像法
所谓的行图像法,其实就是将这个方程组按照行去切成两块👇
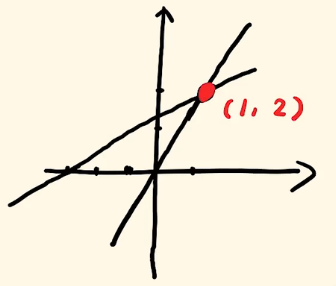
这样就成了两根直线,现在我们把它给描绘出来👇
我们可以发现,这两根直线有一个交点(1,2),我们把这个交点当做方程组的解。
这是一种高中常用的方法。但是线性代数中我们通常不用这种方法,我们通常用列图像法👇
2、列图像法
列图像法就是,我们可以将上面这个方程组转换成矩阵乘法的形式,把它的系数拿出来,乘以x和y,等于右边的列向量。如下图👇
下面我们来看一下这个“列图像”是怎么玩的
上图👆中,我们把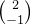
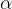
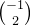
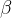
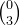
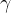
如果你还记得一点点矩阵相乘的知识,那么上面就等于:
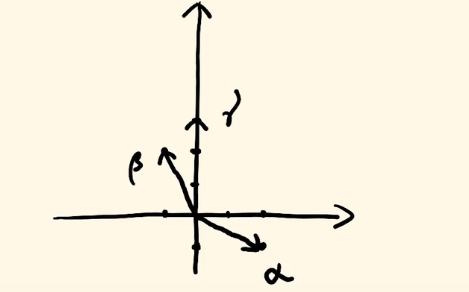
用向量来表示,就如下图👇
翻译一下上面图的意思:就是多少倍的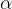
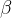
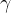
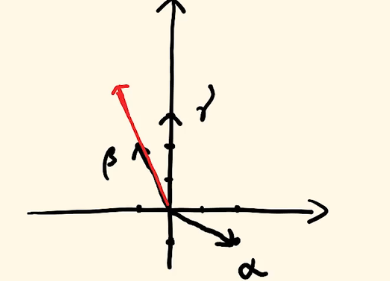
因为我们刚才已经解出来了,x=1,y=2,那么也就是👇
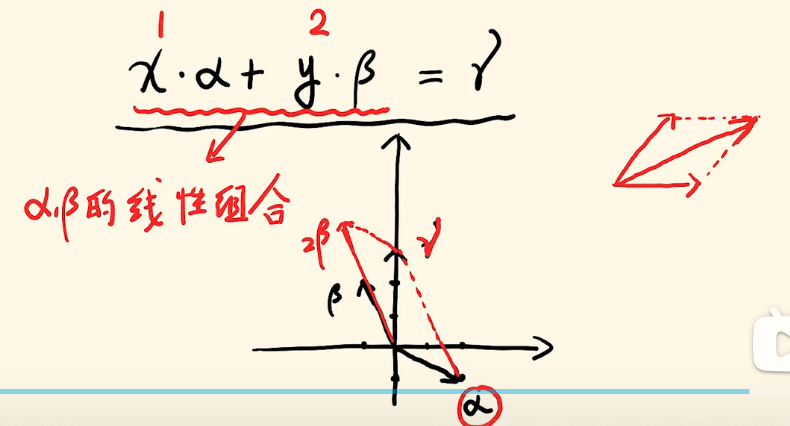
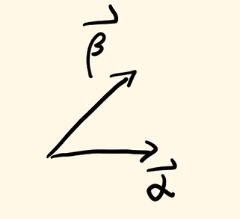
向量的相加和我们高中物理的力的合成和分解是一样的,都遵循平行四边形法则。即:
也就是说,我在解上面这个方程组的时候,其实就是在看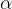
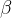
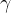
所以向量之间的关系和方程组是密不可分的。一开始我也提到,第三章向量组,第四章方程组,它们之间是有很强的联系的,现在我把这个联系告诉你们了:解方程其实就是在做线性组合。
总结一下,今天我们聊了两个预备知识:
1、向量,向量是一个有大小、有方向的量,并且它可以在坐标轴中用类似于点的坐标的形式表示出来。
2、线性方程组,这个是我们都很熟悉的,我们介绍了解方程组的两种方法:行图像法、列图像法。而通过列图像法可以发现,解方程组其实和找向量的线性组合这两者是统一的。
视频2:向量与空间
原视频:线性代数预备知识——向量与空间_哔哩哔哩_bilibili
上个视频我们聊了向量和线性方程组,我们知道向量是可以表示一个力的大小、方向。同时向量与方程组之间也有着密不可分的关系。那向量还可以用来做什么呢?向量可以用来表示一个空间。接下来我们来聊聊它是如何表示一个空间的。
一、空间(space)
我们先来聊一聊什么是空间。我相信大家对于空间这个概念还是比较熟悉的,比如一维空间是一条直线,二维空间是一个平面,三维空间是我们所属的空间,四维空间是我们作为三维空间的生物所无法想象的。
空间维度的数学表示方法如下:
二、坐标
我们以前用到的坐标一般都是在直角坐标系中的,如下图:
问:什么是坐标?
答:坐标其实就是定位一个点的方法。
其实我们定位点不一定只有一种方法。除了我们常用的直角坐标系(笛卡尔坐标系)以外,我们还有极坐标,三维里面还有球坐标、柱面坐标等等。这里不做过多的拓展。我们就来看这个直角坐标。
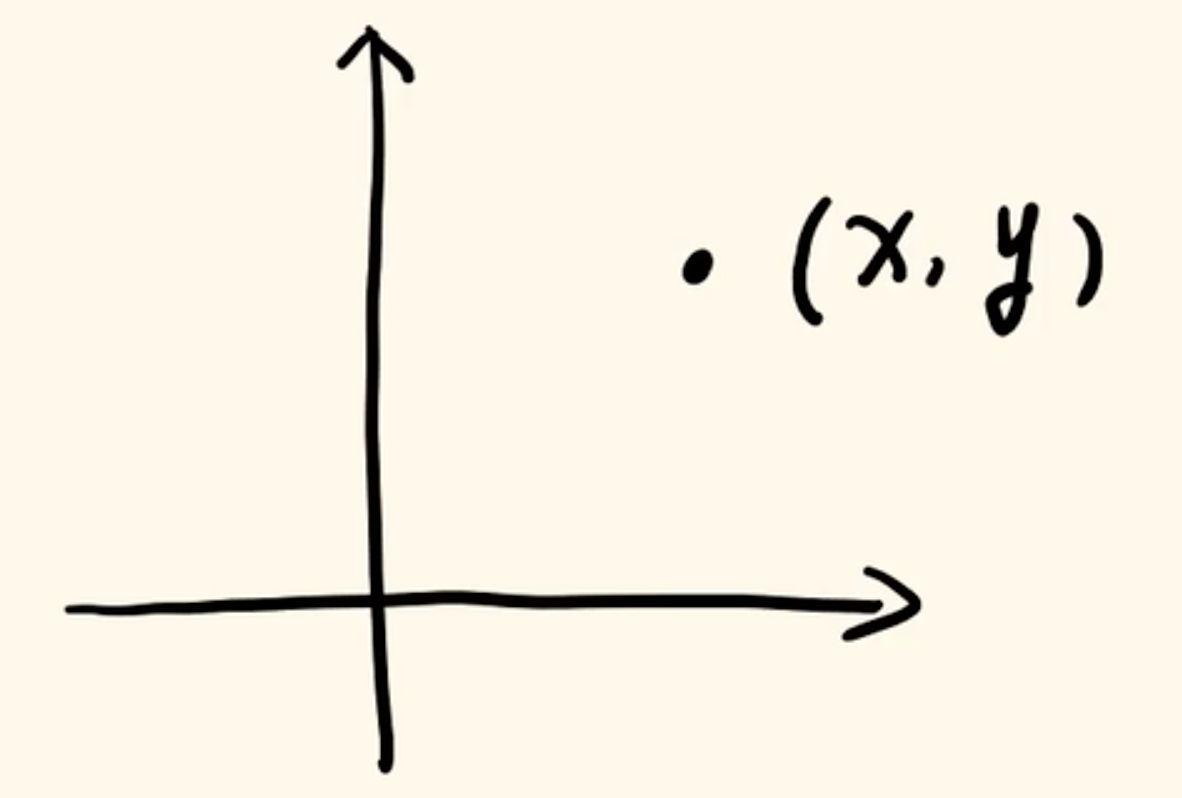
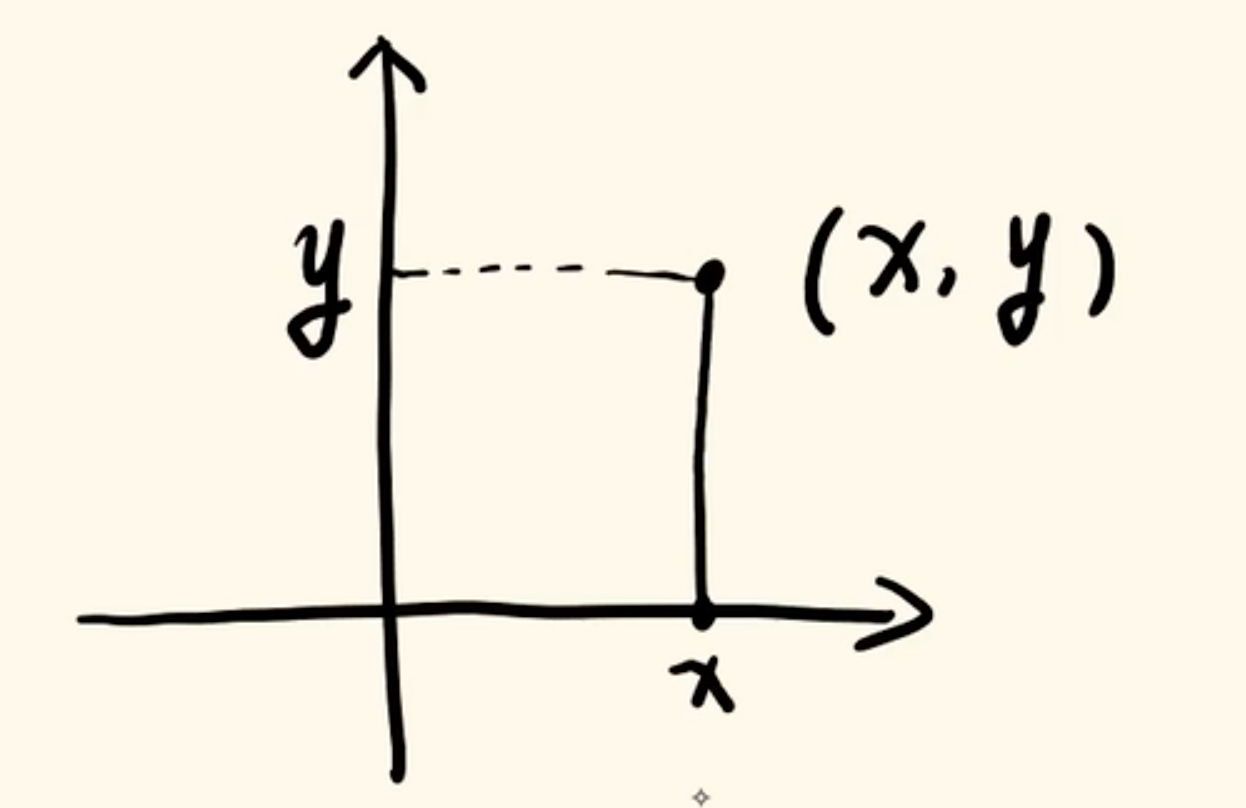
你们有没有想过直角坐标中的(x,y)究竟是什么?怎么得到这个坐标的?你大概率可能会说,这个点对x、y轴分别做一个投影,长度分别是x、y。然后就说这个点的坐标是(x,y)如下图⬇️
这样想当然没错,但你有没有想过它实际上是什么呢?
如下图⬇️,这个点我已经改成了向量形式
之前我们说过,在线性代数里面,我们研究一个点,往往不是研究这个点本身,而是研究它所对应的那个向量。那我们来看这个向量是哪里来的。
我给大家两个向量: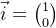
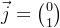
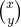
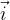
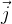
接下来,请大家思考这样一个问题: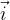
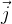
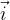
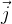
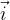
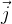
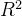
那下一个问题,各位想一想,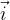
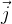
请问这两个向量可以像刚才那样表示出整个平面吗?答案是肯定的,我们只需要看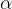
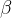
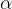
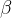
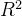
那么,,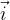
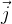
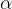
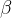
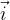
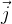
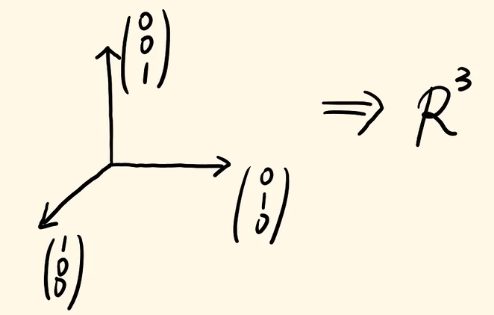
听完这些内容之后,你脑子里再想想三维的直角坐标系,可以说,下图中的这三个向量张成了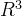
以上就是向量与空间的一些预备知识,希望这些预备知识能让你对线性代数有一个初步的、直观的理解,而不是仅仅停留在觉得线性代数只是一门纯计算的课,觉得它是一个数字游戏。接下来的视频中,我会挑一些在授课过程中同学们遇到问题比较大的,或者问的比较多的一些问题,来进行重点的讲解。