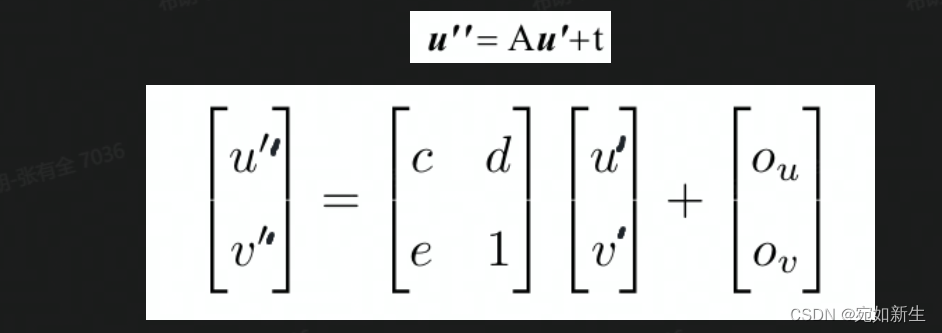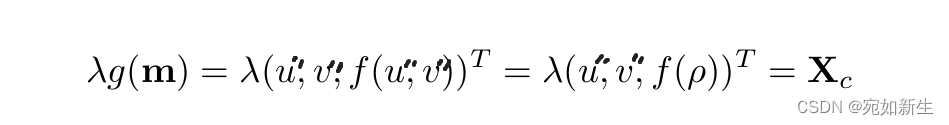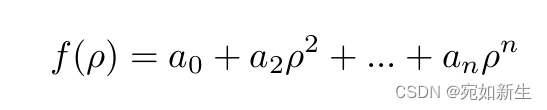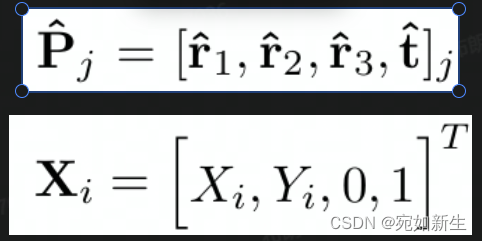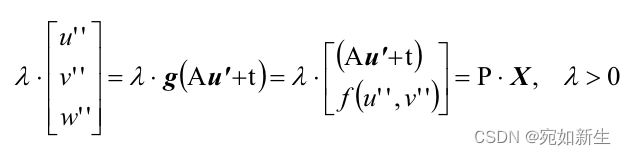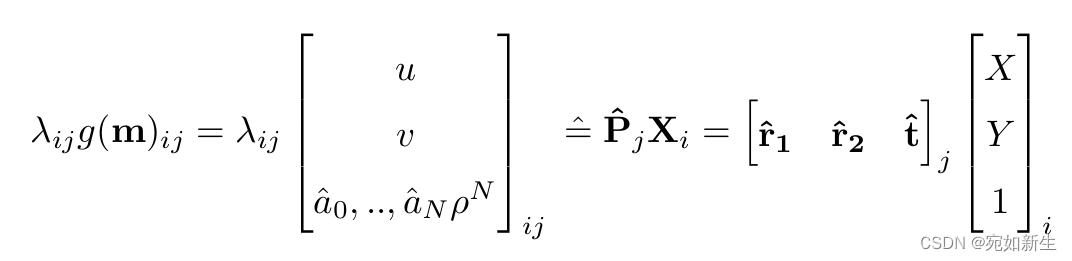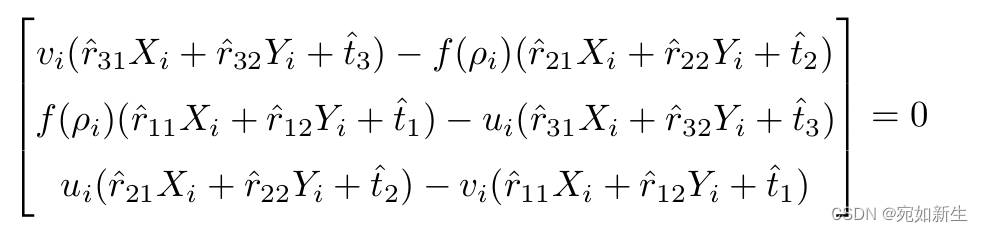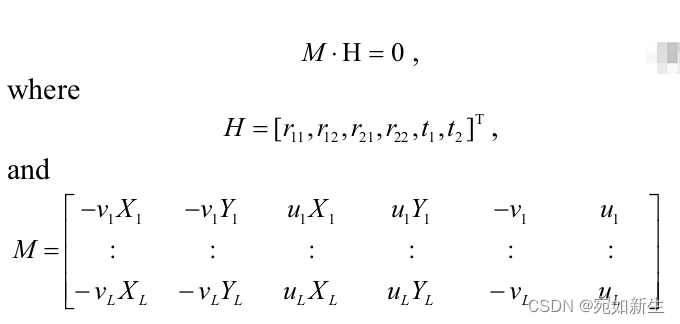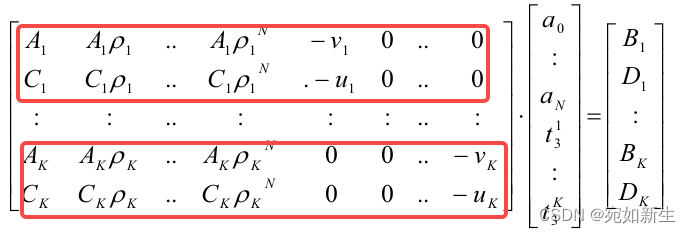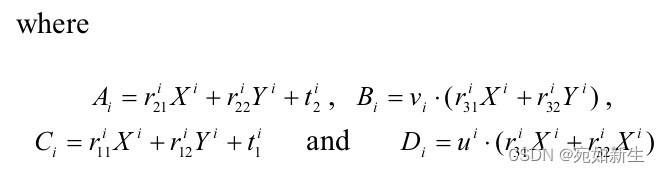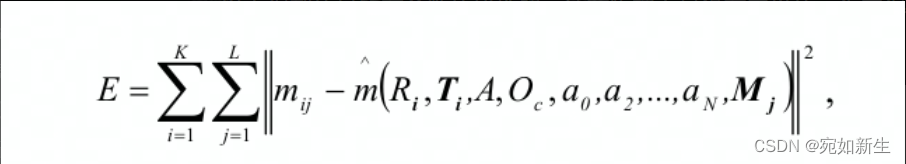1. 定义:
全向相机(Omnidirectional Camera Model)是在水平面上具有360度视野,或具有覆盖半球或(近似)整个球体的视野的相机。
大多数商用相机都可以描述为针孔相机,通过透视投影进行建模。然而,有些投影系统的几何结构无法使用传统针孔模型来描述,因为成像设备引入了非常高的失真。全向相机系统就是其中一种。
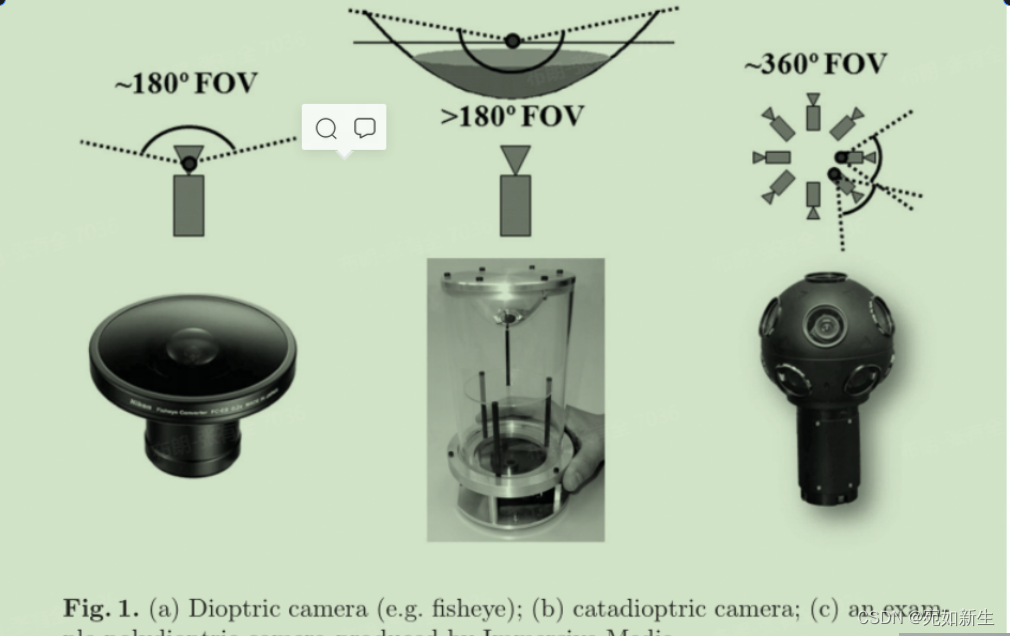
(1)屈光照相机(Dioptirc cameras)使用成形透镜的组合(例如鱼眼透镜,图1a),并且可以达到甚至大于180度的视野(即略大于半球)。
(2)折反射相机(Catadioptric cameras)将标准相机与成型镜(如抛物面镜、双曲面镜或椭圆镜)相结合,在水平面上提供360度的视野,在仰角(elevation)上提供100度以上的视野(图1b)。
(3)多折射相机使用多个具有重叠视场的相机(图1c),迄今为止是唯一提供真正全向(球形)视场的相机。
2. scaramuzza多项式模型
直观地说,全向相机的模型比标准透视相机稍微复杂一点。该模型确实应该考虑折反射相机的镜面反射,或者鱼眼相机的镜头折射。
目前有两种全向相机模型标准:
第一种模型称为中央折反射相机的统一投影模型。优点是提出了一个包括所有三种类型的中央折反射相机的模型,即使用双曲镜、抛物面镜或椭圆镜的相机。这个模型是专门为中央折反射相机开发的,但对鱼眼相机无效。
第二种模型将中心折反射相机和鱼眼相机统一在一个通用模型下,也称为泰勒模型。它由Scaramuzza等人在2006年开发,其优点是折反射相机和屈光相机都可以用同一个模型来描述,即一个泰勒多项式。这里讲解的是这种模型,参考论文:A Flexible Technique for Accurate Omnidirectional Camera Calibration and Structure from Motion。
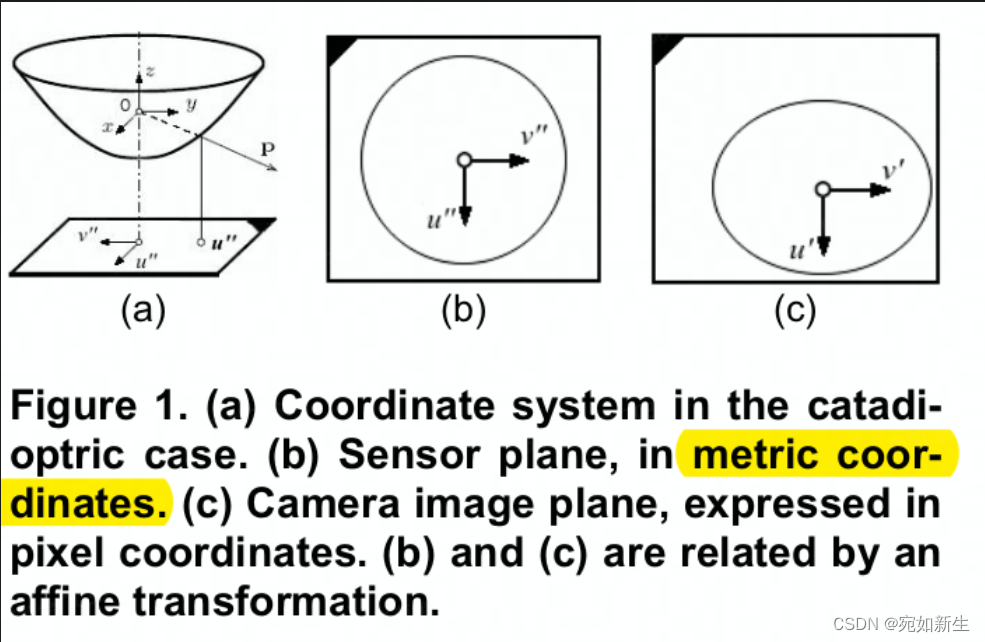
在图1中显示了折反射相机系统(Catadioptric cameras)的两个参考平面。在屈光情况下,由于没有反射面,u”的符号会颠倒。所有坐标将表示在O放置的坐标系中,z轴与传感器轴对齐。
2.1 模型推导
很容易理解上图中(b)(c)两者存在一个仿射变换:
于是有下面完整的模型表达:
Xc是空间中点在相机坐标系的齐次表示;m表示归一化平面上点的坐标(u’‘, v’');g图像投影函数表示Sensor plane(其实就是相机归一化平面) 和 从视点O到场景点X的向量p之间的关系。
最终,
从完整的OCAM模型可知,上述模型已经包含了畸变过程,我们要标定的参数为[c, d, e, Ou, Ov, a0, a1, a2, …]。
3. 标定原理
在相机标定过程中,多个相机位姿观察到一个平面的标定板(Z = 0)。位姿、观察到的世界点如下表示。
将其带入ocam相机模型得到如下关系:
3.1 求外参
这里重新用 [u, v] 表示 [u’‘, v’'], 归一化平面的图像点坐标。
求解上式,先消去λ。
由第三个公式可以求出 [r21, r22, r11, r12, t1, t2], 又因为 r1 和 r2 正交,也是可以算出 r31 , r32,t3的求解在下一步骤。
3.2 求内参
现在,我们将估计值代入前两个方程,并解出相机的本征参数a0, a1, a2, …, aN描述的图像投影函数g。同时,也计算出每个姿态的未知t3。把所有未知数展开,用一个向量表示。
一开始把A设置为单位阵,t设置为图像中心。通过优化迭代得到最优值。
至此,所有要标定的参数都得到了。
3.3 非线性优化
以上得到的是所有参数的线性解,这在物理上是没有意义的。为了得到更细化的结果,采用最大似然估计方法。假设用不同位姿采集了K张图片,每张图片上有L个角点:
通过LM方法使得上述重投影误差最小,得到所有参数的最优化结果。