A. Only Pluses

 has three integers 𝑎, 𝑏 and 𝑐 ，has to give Noobish_Monk 𝑎×𝑏×𝑐 bananas.these integers and decided to do the following at most 5 times

pick one of these integers

increase it by 1

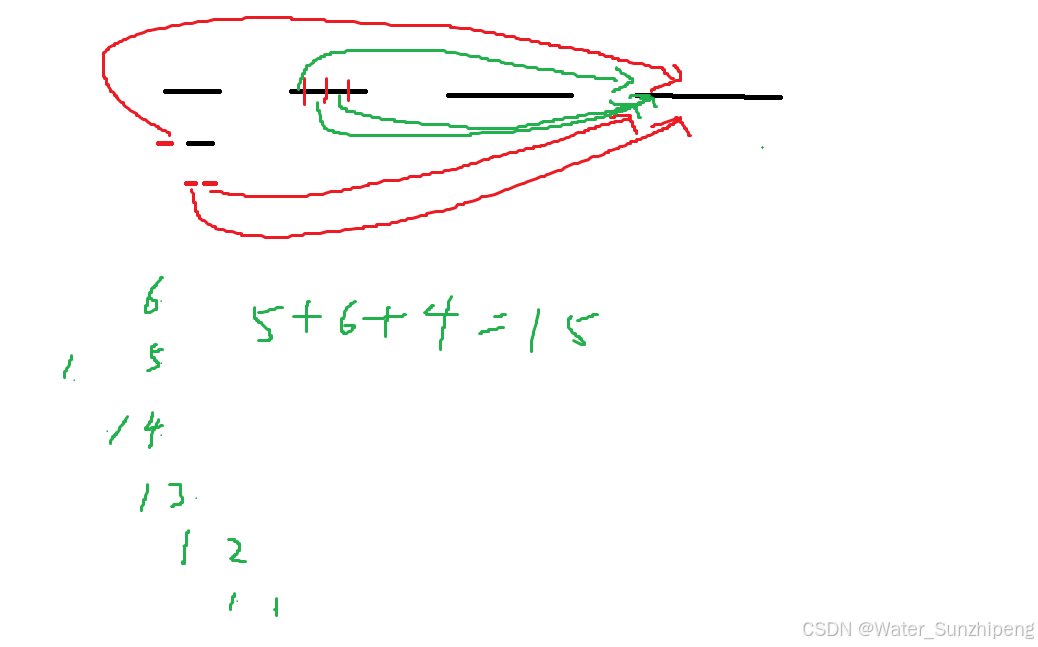
For example, if 𝑎=2, 𝑏=3 and 𝑐=4, then one can increase 𝑎 three times by one and increase 𝑏 two times. After that 𝑎=5, 𝑏=5, 𝑐=4. Then the total number of bananas will be 5×5×4=100.

the maximum value of 𝑎×𝑏×𝑐 

贪心思想，每次找到最小的数 +1，数据范围很小，直接暴力。

#include<bits/stdc++.h>

using namespace std;

#define i64 long long 

void solve(){
	vector<int> a(3);
	for(int i = 0; i < 3; i ++) cin >> a[i];
	for(int i = 0; i < 5; i ++){
		sort(a.begin(), a.end());
		a[0] ++;
	}
    cout << (i64)a[0] * a[1] * a[2] << "\n";
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--)
    	solve();
    return 0;
}

B. Angry Monk

 k1o0n has baked an enormous 𝑛 metres long potato casserole. He has cut it into 𝑘 pieces, of lengths 𝑎1,𝑎2,…,𝑎𝑘 meters.k1o0n wasn't keen on that.

• Pick a piece with length 𝑎𝑖≥2 and divide it into two pieces with lengths 1 and 𝑎𝑖−1. As a result, the number of pieces will increase by 1;
• Pick a slice 𝑎𝑖 and another slice with length 𝑎𝑗=1 (𝑖≠𝑗) and merge them into one piece with length 𝑎𝑖+1. As a result, the number of pieces will decrease by 1.

For example, if 𝑛=5, 𝑘=2 and 𝑎=[3,2], it is optimal to do the following:

• Divide the piece with length 2 into two pieces with lengths 2−1=1 and 1, as a result 𝑎=[3,1,1].
• Merge the piece with length 3 and the piece with length 1, as a result 𝑎=[4,1].
• Merge the piece with length 4 and the piece with length 1, as a result 𝑎=[5].

find the minimum number of operations he needs to do in order to merge the casserole into one piece with length 𝑛.(2≤𝑛≤10^9, 2≤𝑘≤10^5)

The second line contains 𝑘 integers 𝑎1,𝑎2,…,𝑎𝑘 (1≤𝑎𝑖≤𝑛−1, ∑𝑎𝑖=𝑛) 

贪心思想，一直分解除最大数之外的数

#include<bits/stdc++.h>

using namespace std;

#define i64 long long 

void solve(){
	int n, k;
	cin >> n >> k;
	vector<int> a(k);
	for(int i = 0; i < k; i ++)	cin >> a[i];
	sort(a.begin(), a.end());
	i64 res = 0;
	for(int i = 0; i < k - 1; i ++){
		if(a[i] == 1)
			res += 1;
		else{
			res += (a[i] + a[i] - 1);
		}
	}
	cout << res << endl;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--)
    	solve();
    return 0;
}

C. Gorilla and Permutation

 three numbers 𝑛, 𝑚, and 𝑘 (𝑚<𝑘).  construct a permutation† of length 𝑛,For the permutation, 𝑔(𝑖) is the sum of all the numbers in the permutation on a prefix of length 𝑖 that are not greater than 𝑚

𝑓(𝑖) is the sum of all the numbers in the permutation on a prefix of length 𝑖 that are not less than 𝑘.

find a permutation for which the value of (∑ni=1f(i)−∑ni=1g(i)) is maximized.(2≤𝑛≤10^5; 1≤m<k≤n)

使得f()最大，大的在前面，g()最小，小的在前面

#include<bits/stdc++.h>

using namespace std;

#define i64 long long 

void solve(){
	int n, k, m;
	cin >> n >> m >> k;
	for(int i = 0; i < n - m; i ++){	
		cout << n - i << " ";
	}
	for(int i = 0; i < m; i ++)
		cout << i + 1 << " \n"[i == m - 1];
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--)
    	solve();
    return 0;
}

D. Test of Love

 We decided to test this love. ErnKor will have to swim across a river with a width of 1 meter and a length of 𝑛 meters.Therefore, in total (that is, throughout the entire swim from 0 to 𝑛+1) ErnKor can swim in the water for no more than 𝑘 meters.

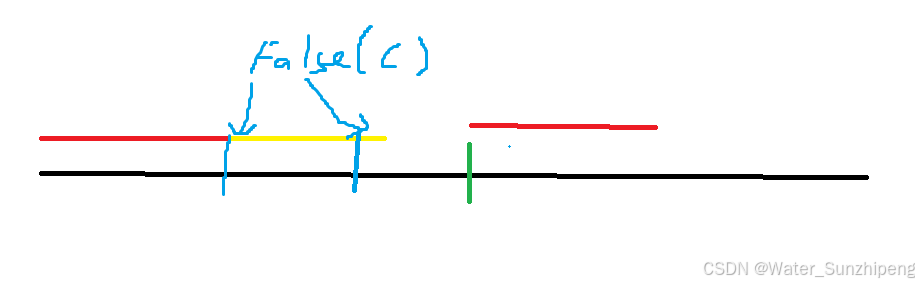
They are located at the 0 and 𝑛+1 meters respectively. The river can be represented as 𝑛 segments, each with a length of 1 meter. Each segment contains either a log 'L', a crocodile 'C', or just water 'W'. ErnKor can move as follows:

• If he is on the surface (i.e., on the bank or on a log), he can jump forward for no more than 𝑚 (1≤m≤101≤𝑚≤10) meters (he can jump on the bank, on a log, or in the water).
• If he is in the water, he can only swim to the next river segment (or to the bank if he is at the 𝑛-th meter).
• ErnKor cannot land in a segment with a crocodile in any way.

p < n卡我很长时间，也是贪心思想，找到最近的L，动态更新

#include<bits/stdc++.h>

using namespace std;

#define i64 long long 

void solve(){
	int n, m, k;
	cin >> n >> m >> k;
	string tmp;
	cin >> tmp;
	string s = " " + tmp;
	int p = m;
	int i = 1;
	while(p <= n){
		for(int j = i; j <= p && p <= n; j ++){
			if(s[j] == 'L')
				p = j + m;
		}
		if(p > n)
			break;
		while(p <= n && s[p] == 'W' && k >= 0){
			k --;
			p ++;
		}
		
		if(k < 0 || ( p <= n && s[p] == 'C')){
			cout << "No" << endl;
			return;
		}else
			i = p;

	}
	cout << "Yes" << endl;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--)
    	solve();
    return 0;
}