51Nod - 1294 修改数组

问题描述：

给出一个整数数组A，你可以将任何一个数修改为任意一个正整数，最终使得整个数组是严格递增的且均为正整数。问最少需要修改几个数？

输入：

第1行：一个数N表示序列的长度(1 <= N <= 100000)。 第2 - N + 1行：每行1个数，对应数组元素。(0 <= Ai <= 10^9)

输出：

输出最少需要修改几个数使得整个数组是严格递增的。

样例输入：

5
1
2
2
3
4

样例输出：

3

解题思路：

在所有元素大于等于0的情况下，我们要求使得一个数组严格递增的最少修改次数，那么我们可以考虑一种最极端的情况，那就是1，2，3，4，…，n，这个是最小严格递增子序列。对一个数组A来说，若A[i] < i，那么第i个位置是一定要被修改的，因为它连最小严格递增子序列在 i 位置的大小 i 都不满足。
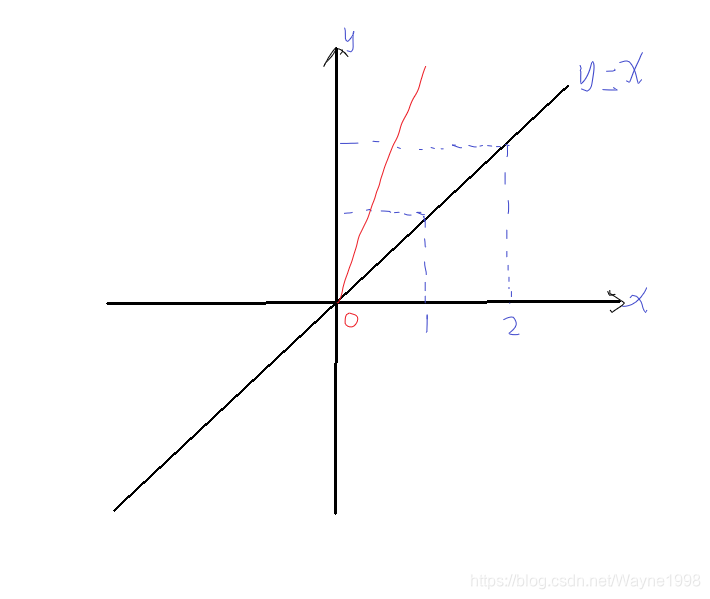
在确定了这些不满足最小严格递增子序列的数之后，我们还要考虑哪些数呢？其实我们可以画一个直角坐标系，如下图所示：

观察这个直角坐标系，我们可以发现，若要使得修改后的数组A满足严格递增的条件，数组A上的所有点形成的直线一定是位于y = x的上方的，即直线斜率大于等于1，那么有：(y1 - y2) / (x1 - x2) >= 1，即：y1 - x1 <= y2 - x2。也就是对所有的a[i] - i >= 0来说，我们需要找到一个由某些a[i] - i 所构成的最长非下降子序列。那么接下来要做的是求最长非下降子序列即可。

求解过程分为以下几步：
1.对数组A做处理，将其变为由A[i] - i 所构成的数组。
2.对新数组中大于等于0的项，求他们的最长非下降子序列的长度，使用二分降低时间复杂度。
3.除了这个最长非下降子序列中的元素外，其余的元素都是要被修改，用n减掉这个最长非下降子序列的长度就是最终答案。

代码实现：

#