直接选择排序（Straight Selection Sort），是一种比较简单的选择排序方法。它的基本思想是：第一次从待排序的序列中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。在直接选择排序过程中存在大跨度的数据移动，选择排序是不稳定的排序方法

要点：每一次循环都选出未排序号序列中最小（大）元素，然后放在已排序好的末尾

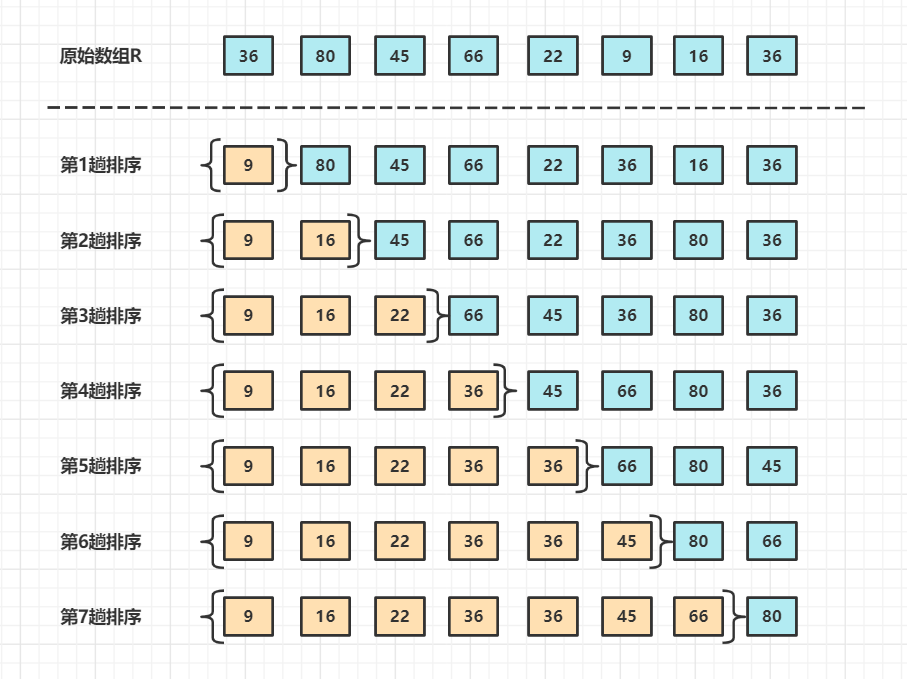
测试用例： 使用直接选择排序算法将数组 { 36，80，45，66，22，9，16，36 } 进行升序排序

代码实现

    /**
     * 直接选择排序
     * @param nums 数组
     * @param size 数组大小
     * @return 返回排列好的数组
     */
    public int[] StraightSelectionSorting(int[] nums, int size){
        int position;   // 用于循环遍历数组的下标
        int min, temp, j;   // min最小值的下标,temp用于将最小值与当前循环position下标的值交换使用
        for (position = 0; position < size - 1; position++) {   // 循环遍历数组
            min = position;     // 获取当前元素的下标
            for (j = position + 1; j < size; j++) {     // 寻找当前未排序序列中的最小值
                if (nums[min] > nums[j])
                    min = j;
            }
            if (position != min) {      // 如果当前最小值的位置与外循环位置的初始值不一致,则需要交换两个元素的位置
                temp = nums[position];  // 说明还有比position位置的值更小的元素
                nums[position] = nums[min];
                nums[min] = temp;
            }
        }
        return nums;
    }

时间复杂度：元素的比较次数和序列中的初始记录无关，其比较次数为：$$\sum _{i=1}^{n-1}(n-i)$$ = $\frac{1}{2}{n}^2$ - $\frac{1}{2}n$，总交换次数不超过 $n-1$ 次。当待排序初始序列为正序时，不发生交换；当初序列为逆序时，发生 $n-1$ 次交换，即移动次数最多 $n-1$ 次。因此，直接选择排序的平均时间复杂度为$O(n^2)$

空间复杂度
在直接选择排序的过程中，只需要一个元素大小的辅助空间用于存放待插入的元素，因此空间复杂度为$O(1)$