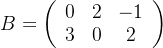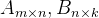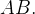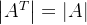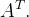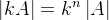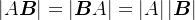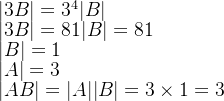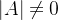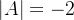1.矩阵的运算
1.1.定义
| 矩阵 | 行列式 |
| 数表 | 数 |
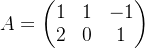 |
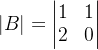 |
| 行数和列数可以不相等 | 行数和列数必须相等 |
1.2.加法与数乘
矩阵的数乘:所有元素都乘这个数
矩阵的加法:对应位置处元素相加
🦊已知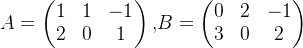
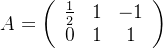
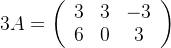
1.3.乘法
矩阵乘法三步法
①
能不能乘:内定乘
②
乘完是何类型:外定型
③
中的元素是什么:左出行,右出列
🦊已知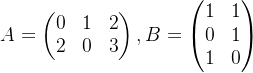
由于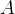
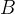

1.4.转置
矩阵
的转置,就是将矩阵
行列互换后得到的矩阵。
🦊已知矩阵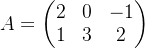
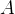
矩阵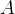
矩阵
1.5.方阵的行列式
方阵行列式的公式:
🦊设
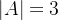
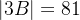
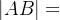
🦊设
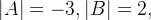
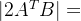
根据公式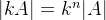

根据公式
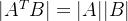
所以
2.矩阵的求逆
逆矩阵就相当于矩阵的“倒数”,对于一个方阵(行数和列数相等的矩阵)
,如果存在另一个矩阵
,使得
乘以
等于单位矩阵
(单位矩阵就像数字中的
,主对角线上都是
,其他位置都是
),那么
就是
的逆矩阵,记作
。
可逆的充要条件
矩阵
可逆的充要条件是
🦊已知矩阵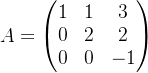
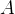
由于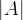
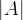
即
由于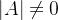
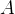
2.1.伴随矩阵法(二阶具体方阵求逆)
伴随矩阵
伴随矩阵主要用于求逆矩阵,因为有一个重要的公式
,其中
是矩阵
的行列式。当
时,就可以通过这个公式利用伴随矩