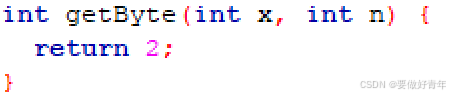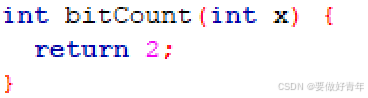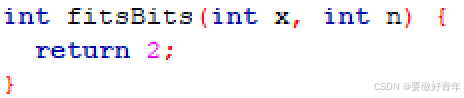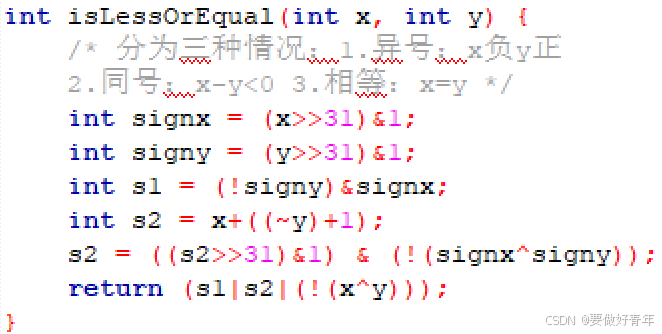写在前面
以下是实验二的报告,其中对每个函数的讲解自认为还是比较清晰的,仅供交流学习使用哦。
1 实验项目
1.1 项目名称
实验2 DataLab
1.2 实验目的
(1)完善 bits.c 里的各个函数,实现其功能;
(2)使bit.c通过btest中的所有测试,同时不违反任何编码准则;
(3)增强对二进制数及其操作的理解。
1.3 实验资源
(1)教材中datalab的相关内容;
(2)Readme文件中的实验说明;
(3)实验文件夹中相关的各文件及程序;
(4)bits.c源文件中的注释说明;
(5)dlc和btest两个测试工具
1.4 实验要求
(1)整数编码规则
1. 只能使用整数常量 0 到 255(0xFF),包括0。不允许使用诸如 0xffffffff 之类的大常量;
2. 只能使用函数参数和局部变量(不允许使用全局变量);
3. 只能使用一元整数操作符 ! ~ 和二元整数操作符 & ^ | + << >>,不能使用任何其他操作,如 &&、||、- 或 ? :
4. 不能使用任何控制结构,如 if、do、while、for、switch 等;
5. 不能使用除 int 之外任何数据类型。即也不能使用数组、结构、联合;
6. 不能定义或使用任何宏,不能定义任何其他函数也不能调用任何函数;
7. 不能使用任何形式的类型转换;
8. 对整数进行算术右移;
9. 使用运算符数不超过限制(Max ops)。
(2)浮点数编码规则
1. 允许使用循环和有条件的控制语句,如 for while if ;
2. 可以使用 int 和 unsigned,但不允许使用其他数据类型;
3. 可以使用任意整数和无符号常量;
4. 不能使用任何浮点数据类型、操作或常量;
5. 不能定义或使用任何宏,不能定义任何其他函数也不能调用任何函数;
6. 不能使用任何形式的类型转换;
7. 使用运算符数不超过限制(Max ops)。
(3)测试要求
完成 bits.c 中的函数编写后,使用 ./dlc 检查代码是否符合编码规范(每个函数都有一组最大操作符限制,由 dlc 检查最大操作符数量。注意 ' = ' 不计数),make btest 进行编译,最后使用 ./btest 进行函数测试。
2 实验任务
2.1 bitAnd
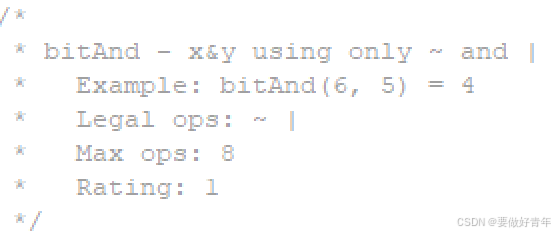
(1) 题目要求
使用按位或和按位取反操作实现按位与操作。
题给限制如下:
题给函数体如下:
(2) 解题过程
利用离散数学中所学的德摩根律思想,将按位与操作用按位或和按位取反操作来实现。德摩根律如下:
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
make btest时有一个警告,原因是里面定义的errors没有用上,也从侧面说明函数都成功实现,没有错误。
由检查结果可知,函数实现正确。
2.2 getByte
(1) 题目要求
将一个字(4字节)的字节从低位起依次编号为0 ~ 3,函数从字中提取出第n个字节。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是从参数x(32位)中取第n个字节(8位)。由于参数x被分成了四份,从低字节开始字节被编号为0~3,要想取出编号为n的字节,先要把参数x右移n个字节,也就是右移8*n位,这样我们需要的字节就在最低8位。然后再将右移后的数与0xFF相与,即保留低8位,并把高24位清零,最后得到我们需要的字节。
以题中的0x12345678为例,先右移8*1(1<<3)位后得到0x00123456,再与0xFF相与,得到0x00000056,即我们需要的字节0x56。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.3 logicalShift
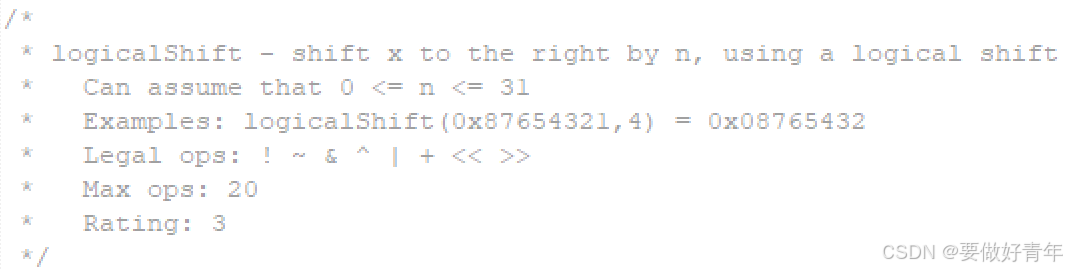
(1) 题目要求
使用逻辑右移将 x 向右移动 n 位。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是将参数x逻辑右移n个bit。在前述的整数编码规则中,8明确规定了对整数进行算术右移,因此要注意这里的逻辑右移与算术右移的区别。逻辑右移时高位要补0,而算术右移时高位要补对应数的符号位。对于正数来说这两种右移方式一样,但对于负数来说,就需要考虑将其高位变0。而这里的参数x可正可负,因此我们主要要考虑其为负数的情况。思路是将其参数x先右移n个bit后,再与0000…1111(n个0)相与,即可将高位变0,从而将算术右移转换为逻辑右移。
那么,进一步地,如何得到0000…1111(n个0)呢?我们可以先将1左移31位得到0x80000000,再将其右移n-1位得到1111…0000(n个1),最后取反得到0000…1111(n个0)。
如题给例子,将0x87654321逻辑右移4位。我们先将1左移31位得到0x80000000,再将其右移4-1=3位得到1111…0000(4个1),取反后得到0000…1111(4个0),再与0x87654321算术右移4位的结果相与,即可得到最终结果。
注意,我们右移n-1位的时候,只能先右移n位,再左移1位得到,因为在前述整数编码规则中提到,- 这个运算符不能使用。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.4 bitCount
(1) 题目要求
返回参数x的二进制表示中 1 的数量。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是返回数的二进制表示中1的个数。如果暴力求解即一位位与上0x1最终得到结果的话,需要用到for循环,但是规则上不允许使用循环,因此思考后选择使用二分法。
因为此题较为复杂,接下来用一个具体的实例来解释一下二分法的具体思想及过程。
对32位整数(10110010110111100110100101001111)2,计算其二进制表示中1的数量。
划分:
首先,我们利用二分的思想将其划分为两个16位二进制串,即
1011001011011110 | 0110100101001111
继续二分,划分为四个8位二进制串,即
10110010 | 11011110 | 01101001 | 01001111
继续二分,划分为八个4位二进制串,即
1011 | 0010 | 1101 | 1110 | 0110 | 1001 | 0100 | 1111
继续二分,划分为十六个2位二进制串,即
10 | 11 | 00 | 10 | 11 | 01 | 11 | 10 | 01 | 10 | 10 | 01 | 01 | 00 | 11 | 11
继续二分,得到最终的32个1位二进制,即
1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1
现在子问题就变成了对于一位二进制数来说,1的个数是多少。那么如果它们是1的话,1的个数就是1;如果它们是0的话,1的个数就是0,这是显而易见的。因此,上面的每个1位二进制数就是最小的子问题的答案。那么接下来我们可以开始进行合并了。
合并:
①首先,我们将相邻两位进行合并。对于二进制加法计算,1+1=10,1+0=01,0+1=01,0+0=00。因此,第一次合并后,我们可以得到以下结果:
01 | 10 | 00 | 01 | 10 | 01 | 10 | 01 | 01 | 01 | 01 | 01 | 01 | 00 | 10 | 10
这个结果中共有16个2位二进制数,每个二进制数是由上面的32个1位二进制数两两为一组相加得到的。比如第一组是1|0,相加得到1的个数为1个,因此它的二进制数表示即为01;又如第二组是1|1,相加得到1的个数为2个,因此它的二进制数表示即为10。
那么,对于每一个2位二进制数的含义可以如下解释:
第一组中 1 的个数的二进制表示|第二组中 1 的个数的二进制表示|第三组中1的个数的二进制表示|… …|第十六组中1的个数的二进制表示
还有一个问题,如何在代码中实现这样的操作呢?
我们先给出对应伪代码,再来进行解释。伪代码如下:
首先,我们将原来的x,即
1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1
与上0x55555555(即01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01),这样,我们就可以得到每一组1位二进制数中右边那位的值。在上例中,即得到
00 | 01 | 00 | 00 | 01 | 01 | 01 | 00 | 01 | 00 | 00 | 01 | 01 | 00 | 01 | 01
再将x右移1位,并与上0x55555555,这样,我们就又可以得到每一组1位二进制数中左边那位的值。在上例中,即得到
01 | 01 | 00 | 01 | 01 | 00 | 01 | 01 | 00 | 01 | 01 | 00 | 00 | 00 | 01 | 01
将两数相加,即可得到第一次合并后的结果,即每两位中1的个数:
01 | 10 | 00 | 01 | 10 | 01 | 10 | 01 | 01 | 01 | 01 | 01 | 01 | 00 | 10 | 10
②接下来,我们继续进行合并,将相邻的两个2位二进制结果合并成一组,合并结果如下:
0011 | 0001 | 0011 | 0011 | 0010 | 0010 | 0001 | 0100
对于每一个4位二进制数的含义可以如下解释:
第一组中 1 的个数的二进制表示|第二组中 1 的个数的二进制表示|第三组中1的个数的二进制表示|… …|第八组中1的个数的二进制表示
对应的在代码中实现这样操作的伪代码如下:
代码的含义同理,我们将合并前的x,即
01 | 10 | 00 | 01 | 10 | 01 | 10 | 01 | 01 | 01 | 01 | 01 | 01 | 00 | 10 | 10
与上0x33333333(即0011 0011 0011 0011 0011 0011 0011 0011),这样,我们就可以得到每一组中右边那个2位二进制数的值。再将x右移2位,并与上0x33333333,这样,我们就又可以得到每一组中左边那个2位二进制数的值。最后再将两个值相加,得到最终的第二次合并后的结果,即每四位中1的个数:
0011 | 0001 | 0011 | 0011 | 0010 | 0010 | 0001 | 0100
③接下来,继续进行合并,将相邻的两个4位二进制结果合并成一组,合并结果如下:
00000100 | 00000110 | 00000100 | 00000101
对于每一个8位二进制数的含义可以如下解释:
第一组中 1 的个数的二进制表示|第二组中 1 的个数的二进制表示|第三组中 1 的个数的二进制表示|第四组中 1的个数的二进制表示
对应的在代码中实现这样操作的伪代码如下:
代码含义同理,0x0F0F0F0F即00001111 00001111 00001111 00001111。我们可以得到第三次合并后的结果,即每八位中1的个数:
00000100 | 00000110 | 00000100 | 00000101
④再进行合并,将相邻的两个8位二进制结果合并成一组,合并结果如下:
0000000000001010 | 0000000000001001
对于每一个16位二进制数的含义可以如下解释:
第一组中 1 的个数的二进制表示|第二组中 1 的个数的二进制表示
对应的在代码中实现这样操作的伪代码如下:
代码含义同理,0x00FF00FF即0000000011111111 0000000011111111。我们可以得到第四次合并后的结果,即每十六位中1的个数:
0000000000001010 | 0000000000001001
⑤进行最后一次合并,将相邻的两个16位二进制结果合并成一组,合并结果如下:
00000000000000000000000000010011
这就是最终得到的x的二进制表示中1的个数的二进制表示。
对应的在代码中实现这样操作的伪代码如下:
代码含义同理,0x0000FFFF即00000000000000001111111111111111。我们可以得到第五次合并后的结果,即三十二位中1的个数:
00000000000000000000000000010011
上面这个二进制数即十进制数19,与我们在上面给出的实例32位整数(10110010110111100110100101001111)2中1的个数一致,思路正确。
注意:在前述的整数编码规则中已说明只能使用整数常量 0 到 255(0xFF),不允许使用诸如 0xffffffff 之类的大常量。因此,我们需要使用小整数及运算符进行计算,以得到我们需要的大整数0x55555555,0x33333333,0x0F0F0F0F,0x00FF00FF和0x0000FFFF。
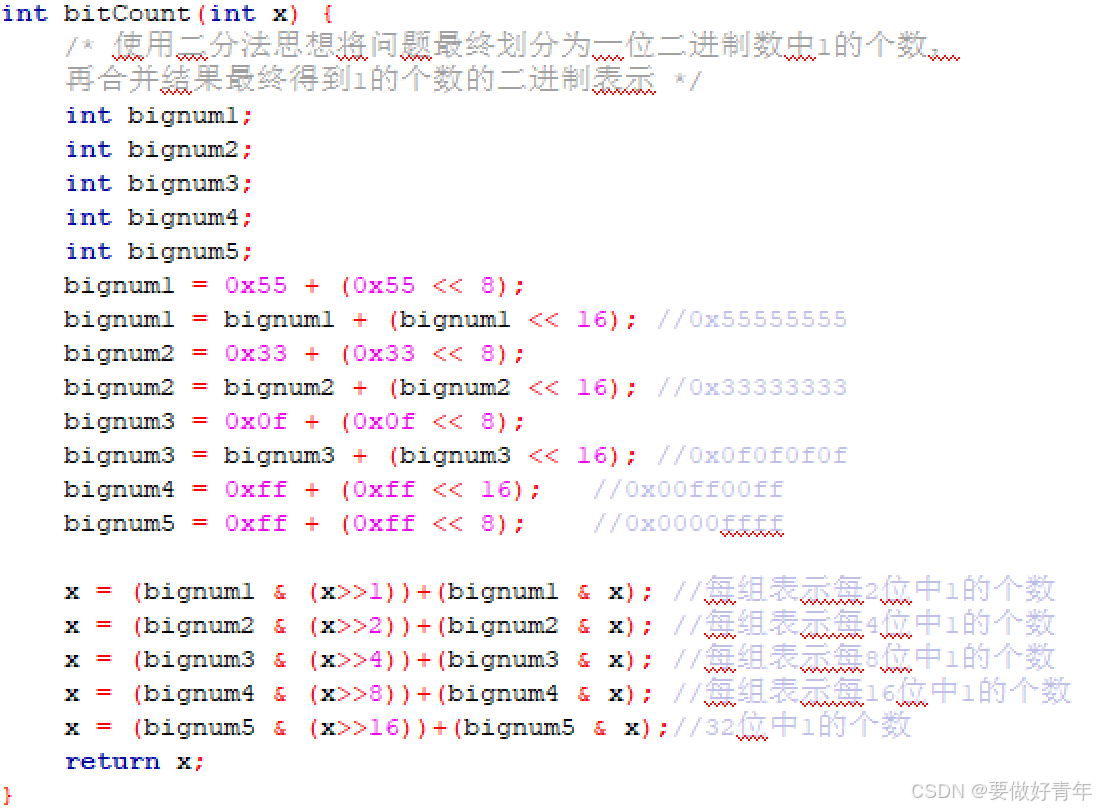
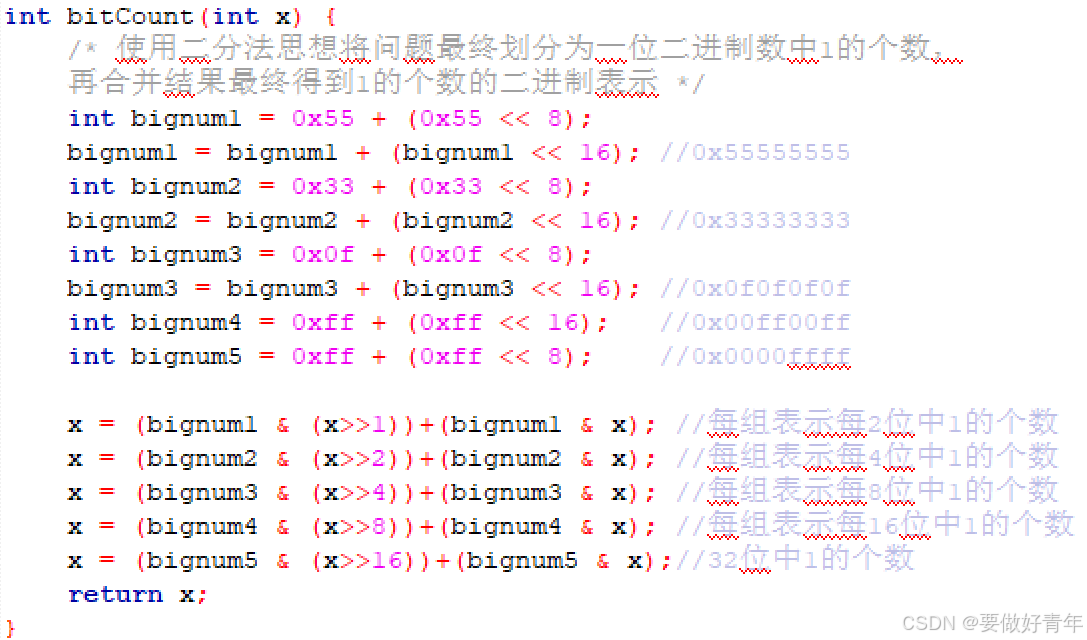
完整函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.5 bang
(1) 题目要求
计算 !x 而不使用 ! 。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是实现逻辑取反操作。如果x为0,则输出1;如果x非0,则输出0。那么,我们首先要做的事情就是将x为0和x非0这两种数分为两种不同的情况。
经过思考,想到了 x | (~x+1) 这个操作。
1. 当 x 为 0 时:
~x 会将 x 的所有位取反,所以 ~0 是全 1 的二进制数。
~x + 1 即 ~0 + 1,也就是全 1 的二进制数加 1。在二进制补码表示中,这会导致溢出,并且结果变为 0(因为全 1 的数加 1 在补码表示中等同于 0)。
因此,x | (~x + 1) 变为 0 | 0,结果是 0。在这种情况下,最高位(符号位)为0。
2. 当 x 不为 0 时:
~x 将 x 的所有位取反。
~x + 1 是对取反后的数加 1,这相当于求 x 的相反数(在二进制补码系统中,-x = ~x + 1)。
x | (~x + 1) 实际上是 x 和 -x 的按位或运算。由于 x 不为 0,x 和 -x 中至少有一个是负数。比如,如果 x 是正数,那它的相反数 -x 就是负数;如果 x 是负数,那它的相反数 -x 就是正数。
而如果 x 是正数,其符号位是 0,其相反数 -x 的符号位就是 1。如果 x 是负数,其符号位已经是 1。
因此,无论 x 是正还是负,x | (~x + 1) 的最高位(符号位)都会是 1。
这样,我们就将x为0和x非0这两种情况分开来了。如果x为0,那x | (~x + 1) 的最高位就会是0;如果x非0,那x | (~x + 1) 的最高位就是1。
然后,我们将经过x | (~x + 1) 操作后得到的数算术右移31位,再进行按位取反操作。在这步之后,如果x为0,就会得到全1;如果x非0,就会得到全0。
最后,我们再将上面得到的结果与上1(0x00000001)后,得到最终的结果(x为0,最终结果即为1;x非0,最终结果即为0)并返回。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.6 tmin
(1) 题目要求
返回最小的二进制补码整数。
题给限制如下:
题给函数体如下:
(2) 解题过程
此题要我们返回最小的二进制补码整数。在 32 位系统中,最小的 int 型有符号数(补码表示)为 0x8000 0000,即 1000 0000 0000 0000 0000 0000 0000 0000,十进制值为-2^31。要编码实现该功能也很简单,直接将1左移 31 位即可得到。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.7 fitsBits
(1) 题目要求
如果 x 可以用 n 位二进制补码整数表示,则返回 1。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数要我们判断参数x(int型,32位)能否用n位的二进制补码进行表示,如果能则返回1,不能则返回0。
对于32位的x来说,如果它能用n位补码表示,说明它的高32-n位均为其符号位(第n位)的扩展,那么我们把x先左移32-n位,再算术右移32-n位恢复它,它应该是不变的。而对于不能用n位补码表示的x来说,它的高32-n位中有的位是有意义的,并不都是符号位的扩展,且其符号位也不是第n位。因此,如果我们把它先左移32-n位,再算术右移回来,它的值会发生变化。这样,我们就成功地将能用n位补码表示的x和不能用n位补码表示的x分成了两种不同的情况。
区分这两种不同情况的方法是,用原来的x与左移右移后的x进行异或操作,如果结果为0表示两数相同,取反输出1;如果结果为1表示两数不同,取反输出0。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.8 divpwr2
(1) 题目要求
计算 x/(2^n) ,其中正数向下取整,负数向上取整(即向0取整)。
题给限制如下:
题给函数体如下:
(2) 解题过程
课上讲过,在计算机有符号整数除法中,除数为2的幂次时,通过右移进行除法得到的结果是向下取整的。即如下图所示:
那么当x为正数时,我们可以直接将x算术右移n位得到x/(2^n),这时得到的结果是向下取整的,也即向0取整,符合题目要求。
但是当x为负数时,直接将x算术右移n位得到x/(2^n)也是向下取整的,对于负数来说这并不是向0取整,因此我们需要加上一个偏移量,使被除数(负数)加上偏移量后再进行除法能得到我们想要的向0取整的结果。
即我们课上所讲的:
同时,我们在被除数为正时不希望x再加上偏移量,因此我们对偏移量还要进行一个分情况讨论。于是,我们可以将x右移31位的值存入一个变量sign,如果x为正数,sign即全0;如果x为负数,sign即全1。再将sign与我们上面得到的偏移量进行按位与操作,即可实现对正的被除数不偏移,而对负的被除数进行偏移。
此外,还有一个特殊情况,当n为0时,此时意思是将被除数除1,应该要得到被除数自身的值。在这里,偏移量2^n-1为0,即也不会对负数进行偏移,满足实际情况。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
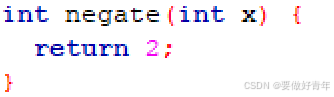
2.9 negate
(1) 题目要求
返回 x 的相反数 -x 。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是返回x的相反数。实现较为简单,根据补码中相反数的计算方法,将x按位取反后加一即可得到其相反数。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.10 isPositive
(1) 题目要求
如果 x > 0,则返回 1,否则返回 0。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是判断x是否为正数,如果是正数则返回1,否则返回0。首先,我们要将数分为两种情况,一种是为0,另一种是不为0。当x不为0时,将x右移31位,如果是正数会得到全0,如果是负数会得到全1。再用逻辑取反操作即可得到返回值1或0。
而当x为0时,也要利用逻辑取反等操作,最终使得函数返回0。
注意,一定要分清逻辑取反操作 ! 和按位取反操作 ~ 的区别。
函数实现如下:
如果x为0,!x即为1,按位或操作后得到的结果一定非0,再逻辑取反得到返回值0;
如果x非0,!x即为0,按位或操作后得到的结果为x>>31。如果x是正数,结果即为全0,再逻辑取反得到返回值1;如果x是负数,结果即为全1,再逻辑取反得到返回值0。
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.11 isLessOrEqual
(1) 题目要求
如果 x <= y,则返回 1,否则返回 0。
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的功能是判断x<=y是否为真。一般来说,逻辑上直接将两数相减,根据所得结果x-y即可判断x<=y是否为真。然而,这里不能仅仅判断x-y的值,因为可能存在溢出,所以需要分情况讨论。
首先,如果两个数异号,并且x为负数,y为正数,那么x<=y即为真,这种情况我们可以直接使用表达式(!signy)&signx表示结果(signx和signy分别是x和y的符号位)。
其次,如果两个数同号且两数不相等,这时我们直接将两个数相减,判断结果的符号即可。两个数同号可以用 !(signx^signy) 来表示。
最后,如果两个数相等,这时可以直接用它们的异或结果来表示。如果两数相等,异或结果为0,逻辑取反后得到返回值1;如果两数不等,异或结果为1,逻辑取反后得到返回值0。
将上述三种情况用逻辑或连接起来即可满足要求。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.12 ilog2
(1) 题目要求
对 x 取以2为底的对数,返回其结果,且向下取整。,其中 x > 0。
题给限制如下:
题给函数体如下:
(2) 解题过程
对x取以2为底的对数,相当于找到x的二进制位模式中,最高位1所在的位置,该位置所代表的2的幂次即为答案。该位置所代表的2的幂次即该位数-1,也即该位的低一位的位数。
那么现在问题就转换成了如何找到x的二进制位模式中,最高位1所在的位置。这个问题也可以用二分的思想来解决。
大致思路如下:先将x分为高16位和低16位,检测高16位,如果高16 位有1,则将指针pointer加上16。接下来将高16位分成25-32位和17-24位,继续检测25-32位,若有1则将指针加上8,没有则不加。不加的话即将17-24位分成17-20位和21-24位,对21-24位进行检测,若有1则将指针加上4,没有则不加。以此类推进行二分操作移动指针,直到最后指针可以定位到最高位1所在的位置的低一位,其位数值即为最终答案。
接下来,我们举个例子来更清楚地说明该做法。
例如,对于二进制数 00000000 10010101 00010101 00101011
我们先将其分为高16位和低16位:
0000000010010101 0001010100101011
首先判断高16位有没有1,显而易见是有的,因此将指针加上16。
代码如下:
二进制数变化如下:( | 代表指针)
00000000 10010101 | 0001010100101011
接下来判断25-32位有没有1,由上数可知没有,因此指针加0。
代码如下:
二进制数变化如下:
00000000 1001 0101 | 0001010100101011
接下来判断21-24位有没有1,由上数可知有,因此指针加上4。
代码如下:
二进制数变化如下:
00000000 10 01 | 0101 0001010100101011
接下来判断23-24位有没有1,由上数可知有,因此指针加上2。
代码如下:
二进制数变化如下:
00000000 1 0 | 01 0101 0001010100101011
接下来判断24位是不是1,由上数可知是,因此指针加上1。
代码如下:
二进制数变化如下:
00000000 1 | 0 01 0101 0001010100101011
最后我们得到的pointer的值即为最高位1所在的位置的低一位的位数23,此即为最终答案。
完整函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.13 float_neg
(1) 题目要求
返回浮点数的相反数,如果结果为NaN,则返回原值。
题给限制如下:
注意,这里允许我们使用任何整数/无符号操作,包括 ||、&&。还有 if、while。
题给函数体如下:
(2) 解题过程
此函数的功能是返回浮点数的相反数,同时题目说明参数和结果都作为无符号整型 unsigned 传递,但它们要解释为单精度浮点值的位级表示。并且,如果参数解释为单精度浮点数后表示NaN,则返回原值。
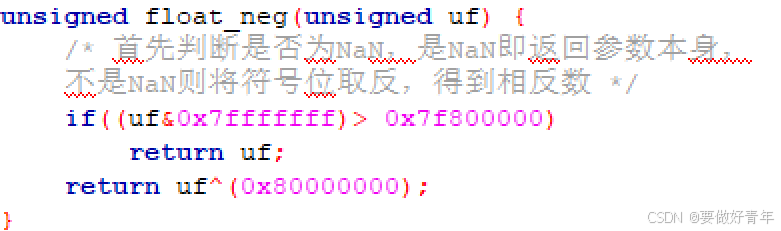
首先,对于不会被解释为NaN的数,将符号位(第32位)取反即可。
而对于NaN,可以通过尾数和阶码使用 if 进行判断,当阶码全1且尾数不为0时,说明是NaN,此时直接返回原值。
判断是否为NaN,我们可以先将参数uf与上0x7fffffff(此时大整数已经可以用了),这会将其最高位置0,同时保留剩下的31位。然后,再将其与0x7f800000(0 11111111 00000000000000000000000)比较大小,如果比0x7f800000大,说明其尾数不为全0,因此其为NaN。此时直接返回uf。
若其不为NaN,就将uf与0x80000000进行异或运算,即可将其符号位(第32位)取反,得到其相反数。
完整函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.14 float_i2f
(1) 题目要求
将整型x转换为浮点数表示。
题给限制如下:
题给函数体如下:
(2) 解题过程
此题要求将整型变量x转换为浮点数形式,并返回其二进制形式。题目说明结果作为无符号整型 unsigned 返回,但它要解释为单精度浮点值的位级表示。
由于此题较为繁琐并且细节较多,接下来直接展示出代码,并且举例逐行进行解释。
函数实现如下:
首先,因为x是补码表示的,如果x为负,它的二进制串不显然,不方便我们向单精度浮点值的位模式进行转换。因此,我们先将所有整型转化为它们的绝对值,并将符号位先单独保存。
将x转化为绝对值时有两种特殊情况,我们需要先单独处理。首先是x为0时,我们直接返回0。然后是x为最小的负数0x80000000时,如果将它转化成它的绝对值,会发生溢出,因此我们直接返回它对应的单精度浮点值的位模式0xcf000000(即1 10011110 00000000000000000000000)。
接下来定义符号位sign,并初始化为0。幂次E,初始化为30。阶码exp,初始化为0。尾数frac,初始化为0。进位carry,初始化为0。
如果x是负数,那么保存符号位0x80000000到sign,并将x取绝对值。
接下来的操作我们举例讲解,假设x为:
0110 1011 0101 0001 0010 1101 1100 0000
将其右移E位(30位)得到:
0000 0000 0000 0000 0000 0000 0000 0001
将其与0x1进行按位与操作后,得到:
0000 0000 0000 0000 0000 0000 0000 0001
它是非0值,说明此时我们找到了x的二进制表示中2的最高幂次位。进行逻辑取反操作后得到0,此时跳出循环。
这时的E就是我们最终的幂次E。根据公式:
我们可以得到单精度浮点数的位模式中,阶码exp的值即E+127(偏置量2^7-1),此处是30+127=157(10011101)。为了后续拼接方便,我们先将它左移23位,使其在它正确的位置即第24-31位上,此时exp即:
0 10011101 00000000000000000000000
接下来,将x左移32-E位,并将左移后的结果赋值给x,这样做是为了暂时抛去x的确定幂次位到最高位,从而专注于尾数的研究。本例中即将x左移2位,更新后x的值为:
1010 1101 0100 0100 1011 0111 0000 0000
因为尾数只有23位,因此要舍去最低的9位。我们先不考虑舍入时的进位,直接将前23位赋值给尾数frac。操作是,先将x右移9位,得到:
1111 1111 1101 0110 1010 0010 0101 1011
再将其与上0x007fffff(即0000 0000 0111 1111 1111 1111 1111 1111),这样做是为了清空右移时候高9位可能出现的1。然后赋值给frac,其为:
0 00000000 10101101010001001011011
接下来我们讨论舍入时的进位,
第一种情况,如果x与上0x01ff的结果(也即x的低9位)大于0x0100,即舍去的值大于保留的最低位所代表的2的幂次的一半,那么就要进位,设置进位符号carry为1。
第二种情况,如果x与上0x03ff的结果(也即x的低10位)等于0x0300,即低10位为11 0000 0000,此时舍去的低9位为中间值,需要向偶数舍入,又因为第10位是1,因此需要进位让第10位变成0。此时也要设置进位符号carry为1。
如果上述两种情况都不满足,那么不发生进位,carry为0。
本例中满足第二种进位情况,因此carry为1。
最后,将 (sign+exp+frac+carry) 的值返回,即为最终我们需要的单精度浮点数的二进制位模式。本例中,即为:
0 10011101 10101101010001001011100
以上是本题完整的分析过程。
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
2.15 float_twice
(1) 题目要求
返回浮点数乘以2的结果.
题给限制如下:
题给函数体如下:
(2) 解题过程
此函数的要求返回浮点数乘以2的结果,同时题目说明参数和结果都作为无符号整型 unsigned 传递,但它们要解释为单精度浮点值的位级表示。并且,对于解释为NaN的情况,直接返回原值。
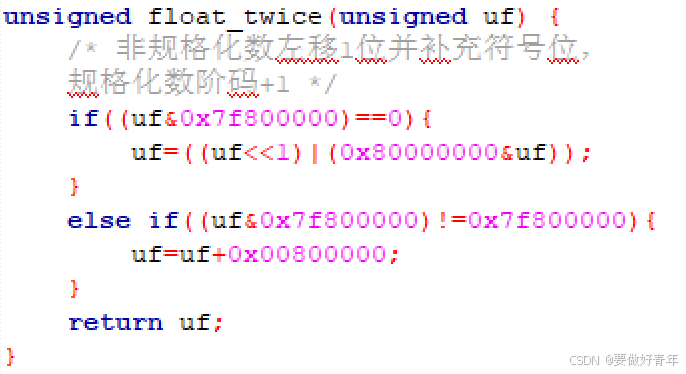
首先,对于非规格化数,由于其可以和规格化数平滑衔接,因此只需要将其左移 1 位,并补充符号位即可。
其次,对于规格化数,要将其×2,只需要将其阶码+1即可,这可以通过将原二进制串加上 0x00800000 实现。
对于其他的值,直接返回原值。
函数实现如下:
接下来先使用dlc编译器检查函数是否符合编码准则:
dlc返回并无错误(error)显示,说明函数符合编码规则。
再使用 btest 测试工具检查函数是否正确,检查过程如下:
由检查结果可知,函数实现正确。
编译及检查
总的编译及检查过程如下:
首先,用./dlc命令对整个bits.c文件进行合法性检验,无报错证明程序内部的编码符合实验要求的编码规范。
运行结果如下
由上图可看出,编译成功并且无错误信息。有一条警告信息,是由于32位乌班图编译器问题,不影响程序结果,在这里可忽略。
接下来,使用./dlc -e bits.c命令查看每个函数使用的运算符数量。
使用make clean清除旧版本的 btest程序,再使用make btest生成新版本的btest。最后用./btest对所有函数进行测试。
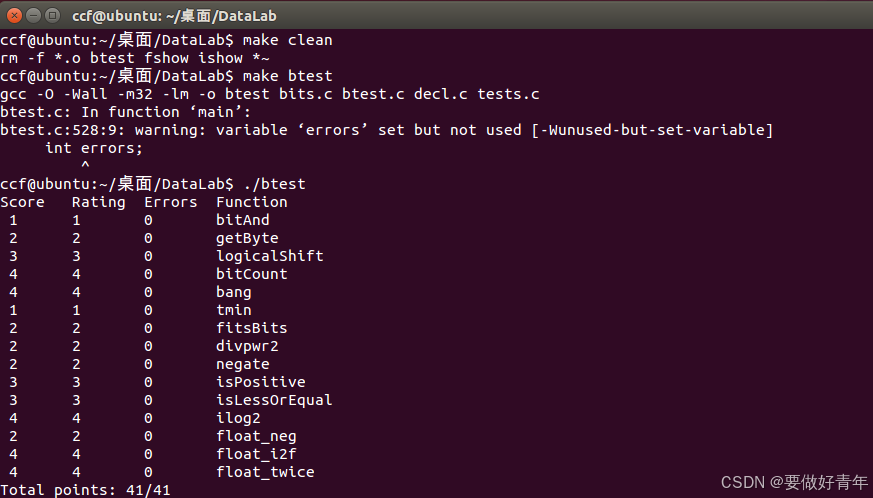
运行结果如下:
make btest在运行时有一个警告的原因是main函数里定义的errors声明了但没有用上,也从侧面说明实验二的所有函数都已经成功实现,没有错误。
由运行结果可知,总得分41分已经拿满并且没有任何错误,说明实验二已成功完成。
3 总结
3.1 实验中出现的问题
1. 在一开始dlc的时候,遇到权限不够的问题。于是使用chmod更改dlc的权限,最终成功运行dlc。
2. 在执行./dlc bits.c时,提示遇到了语法错误。说我有两个函数里的变量没有声明。报错截图如下:
但在回去检查后发现,变量是声明了的。认真观察其他声明变量正确的函数,发现在没有报错的函数中,变量声明都是在函数最开始。因此,推测此dlc工具检查时,只有声明在最开始的变量才能被检测到,而在其他操作之后再声明的变量无法被检测到。
于是,更改函数代码,先声明接下来会用到的变量,再进行其他操作。更新bits.c文件后重新使用dlc工具检查,发现32个错误已经全部解除。
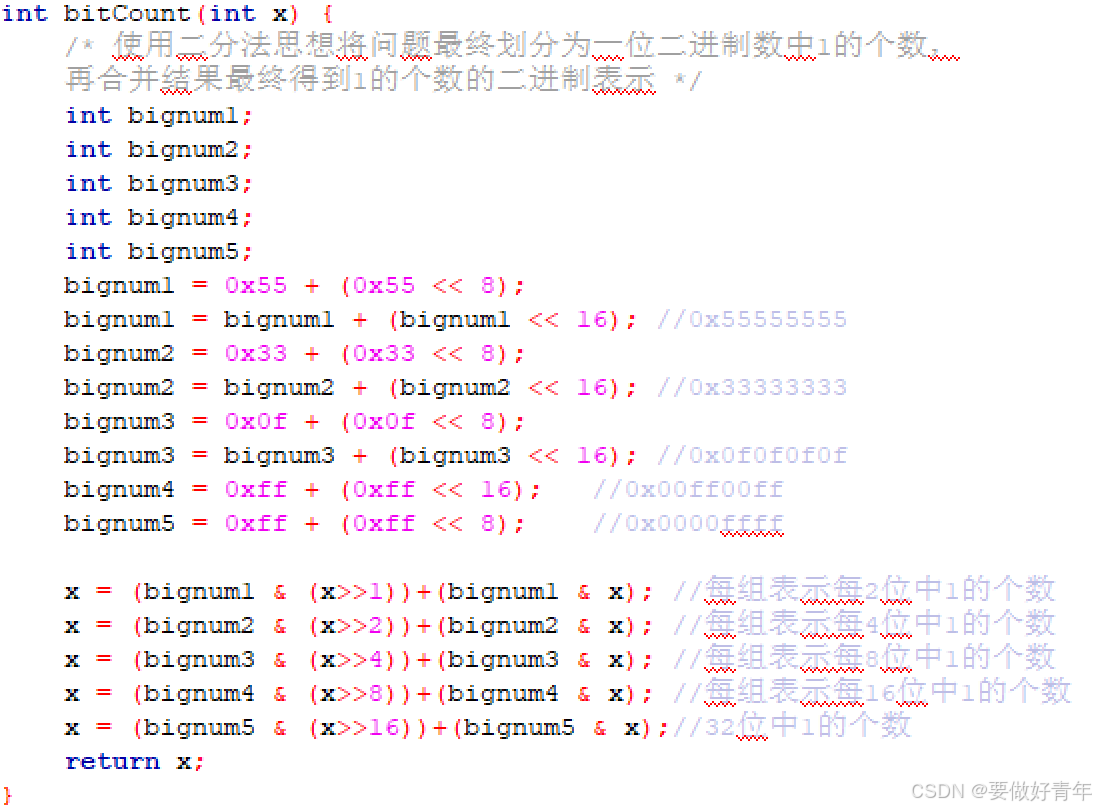
原bitCount函数和更改后的bitCount函数如下:
原float_i2f函数和更改后的float_i2f函数如下:
3. 在上面的函数更改中,虽然修复了32个错误并成功汇编,但仍然有警告信息产生。
以下是在32位乌班图上的警告信息截图:
起初我在思考是不是我函数实现的时候有问题,于是我把从学习通上下载下来的原始文件在32位乌班图上运行,结果还是会出现如上警告信息,说明并不是我函数实现的问题。
后来再使用64位乌班图运行原始文件,没有上述警告信息了。因此推测可能是编译器版本的问题。
在查阅资料后得知,出现这个警告的原因是在编译过程中,预处理器尝试包含一个命令行参数指定的文件,但这个文件不是一个可以被包含的文件。/usr/include/stdc-predef.h 是一个预定义宏的头文件,它通常不需要直接被用户代码包含。有时旧版本的编译器或库可能会导致此类警告。
因此,通过分析以及与助教讨论得出,出现这个警告很大可能是C编译器版本问题。这个警告不影响程序的正常编译和运行,所以通常可以忽略。