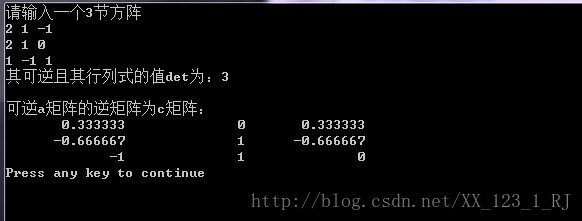
输入矩阵要求为方阵（n×n）

原理：将一个矩阵经过初等行变换化为上三角矩阵一次来求矩阵的行列式，进行行变换求的。

#include<iostream>  
#include<iomanip>     
using namespace std;     
int const n=3;  //确定矩阵的节数    
  
/*  
作者 星星笔记  
  
*/    
  
int main()  
{  
    void temp(double aa[],double bb[],int n);  
    double fun(double array[n][n]);  
    double a[n][n],b[n][2*n],c[n][n],det1,yinzhi;  
    double bb;  
    int i,j,kk=0,k,u;  
    for(i=0;i<n;i++)  //初始化一个辅助矩阵  
        for(j=0;j<2*n;j++)  
            b[i][j]=0;  
    //---------输入原始矩阵---------------  
    cout<<"请输入一个"<<n<<"节方阵"<<endl;  
    for(i=0;i<n;i++)  
        for(j=0;j<n;j++)  
            cin>>a[i][j];   
    //把矩阵a复制给矩阵b  
        for(i=0;i<n;i++)  
          for(j=0;j<n;j++)  
             b[i][j]=a[i][j]; 
		  
       for(j=0;j<n;j++)  
           b[j][n+j]=1;  
    //------------------------------------  
    //------------测试查看----------  
/*     cout<<"a所对应的at矩阵b为："<<endl; 
          for(i=0;i<n;i++) 
           for(j=0;j<2*n;j++) 
            {  
               cout<<setw(6)<<b[i][j]; 
               kk=kk+1; 
               if(kk%(2*n)==0)  
                 cout<<endl; 
             }  */
    //----------------------------------  
//   det1=fun(a);//获取行列式的值  

   for(i=0;i<n;i++)  
   {   
	   // b[i][i] 等于 0 的情况
       if(b[i][i]==0)   
       for(j=i;j<n;j++)  
       {    
           if(b[j][i]!=0)  
             temp(b[i],b[j],2*n);  //交换两行   
       }  
	   // b[i][i] 不等于 0 的情况
       for(k=i+1;k<n;k++)  
       {   
           yinzhi = -1 * b[k][i] / b[i][i];  
           for(u=0; u < 2*n; u++)  
           {   
              b[k][u] = b[k][u] + b[i][u] * yinzhi;  
           }  
      }   
   }  


   det1 = fun(a);//  获取行列式的值  
   if(det1 == 0) //  如果行列式的值为0 则是不可逆的。
   {
     cout<<"此矩阵不可逆："<<endl; 
	 return 0;
   }
   if(det1 != 0)  
   {   
        for(i=0; i<n; i++)    //左矩阵 的对角线 全部 转化为  1
        {  
             bb = b[i][i];   //  bb 不会等于0 因为对角线有有一个为0 说明行列式的值为零，
             for(j=0; j<2*n; j++)  
                b[i][j] = b[i][j] / bb;  
        }  
        for(i=n-1; i>0; i--)  
        for(k=0; k<i; k++)  
        {  
            bb = b[k][i];  
            for(u=0; u<2*n; u++)  
                b[k][u] = b[k][u] - bb*b[i][u];  
        }  
   }  
   //------------测试查看----------  
/*      cout<<"变化后的at矩阵"<<endl;  
      for(i=0;i<n;i++)  
           for(j=0;j<2*n;j++)  
            { 
			 cout<<setw(6)<<b[i][j];  
             kk=kk+1;  
             if(kk%(2*n)==0) 
			   cout<<endl;  
             }        
       cout<<endl;  */
   //------------------------------  
  
   for(i=0; i<n; i++)  
     for(j=0; j<n; j++)  
         c[i][j] = b[i][j+n];  

    kk = 0;  
    if(det1!=0) //输出逆矩阵  
    {     
        cout<<"其可逆且其行列式的值det为："<<det1<<endl<<endl;  
        cout<<"可逆a矩阵的逆矩阵为c矩阵："<<endl;  
  
        for(i=0; i<n; i++)  
        for(j=0; j<n; j++)  
        {    
            cout<<setw(15)<<c[i][j];  
            kk = kk+1;  
            if(kk%n == 0)   
                cout<<endl;  
        }  
    }   
return 0;  
}  
  
void temp(double aa[],double bb[],int n)  
{  //交换数组指定的两行，即进行行变换（具体为行交换）  
    int i;  
    double temp1;  
    for(i=0; i<n; i++)  
    {  
        temp1 = aa[i];  
        aa[i] = bb[i];  
        bb[i] = temp1;   
    }    
}  
  
double fun(double array[n][n])  
{     
    int ii,jj,k,u;  
	int iter = 0;
    double det1=1,yin;  
  
    for(ii=0; ii<n; ii++)  
    {     
        if(array[ii][ii] == 0)   
            for(jj=ii;jj<n;jj++)  
            {    
                if(array[jj][ii] != 0) 
				{
                    temp(array[ii],array[jj],n);//交换两行   
					iter++;
				}
            }  
        for(k=ii+1; k<n; k++)  
        {    
            yin = -1 * array[k][ii] / array[ii][ii];  
            for(u=0; u<n; u++)  
            {  
                array[k][u] = array[k][u] + array[ii][u] * yin;   
            }  
        }  
   }  
  for(ii=0;ii<n;ii++)  
      det1 = det1 * array[ii][ii];  
  if(iter % 2 == 1)
	  det1 = -det1;
    return (det1);      //返回行列式的值  
} 

1.

2.