问题： 

求 {-4, 11，-2, 13，-20，-3，12}的最大子串和，和子串下标？

分析：

既然是求最大子串和那么我们可以肯定的过滤掉第一个正数前的负数。

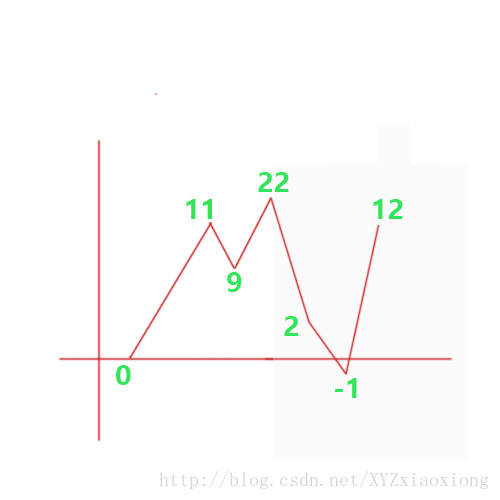
见下图：最大值为22，即所有峰中的最大峰，并且对应的下标为结束下标，而 开始下标即折线过0处下标。

目前该问题的最优解法是动态规划，而Levitin所著的《算法设计与分析基础》第8章告诉我们，有交叠子问题的

问题可以用动态规划技术来解决它。那么该问题的子问题就是 求各”峰“值，我们只需要把”前峰“保存下来和”后峰“

比较即可。递推公式：max{前峰，后峰}；

     

#include<iostream>   
using namespace std;  

int main(){  
	int arr[7]={-4, 11,-2, 13,-20,-3,12};
	int sum=0,max=0;                           //sum前峰值，max后峰值
	int begin=0,end=0;
	for(int i=0;i<7;i++)  
	{  
		if(max>0)  
		{  
			max+=arr[i];              //计算后峰值
		}  
		else  
		{  
			max=arr[i];  
			if(sum<max)               //折线过0后，如果后峰值比前峰值大，重新赋值开始下标
				begin=i;
		}  
		if(max>sum)                       //前后峰进行比较
		{  
			sum=max;                  //保存为前峰值
			end=i;
		}  
	}  
	cout<<begin<<" "<<end<<" "<<sum;
	return 0;  
}