引言

在信号处理领域，自适应滤波器因其能够自动调整参数以优化性能而受到青睐。其中，RLS算法以其卓越的收敛速度和精度，成为了非平稳信号处理的理想选择。本文将探讨RLS算法的基本原理、性能分析、特点以及简单应用，帮助读者理解其背后的数学机制和实际应用场景。

RLS算法基本原理

RLS算法是一种递归算法，它通过最小化误差平方和的代价函数来更新滤波器的权重。与LMS算法不同，RLS使用了指数加权的历史数据，这意味着最近的数据点具有更大的影响，而较早的数据点逐渐被“遗忘”。这一特性让RLS在非平稳环境中表现出色。

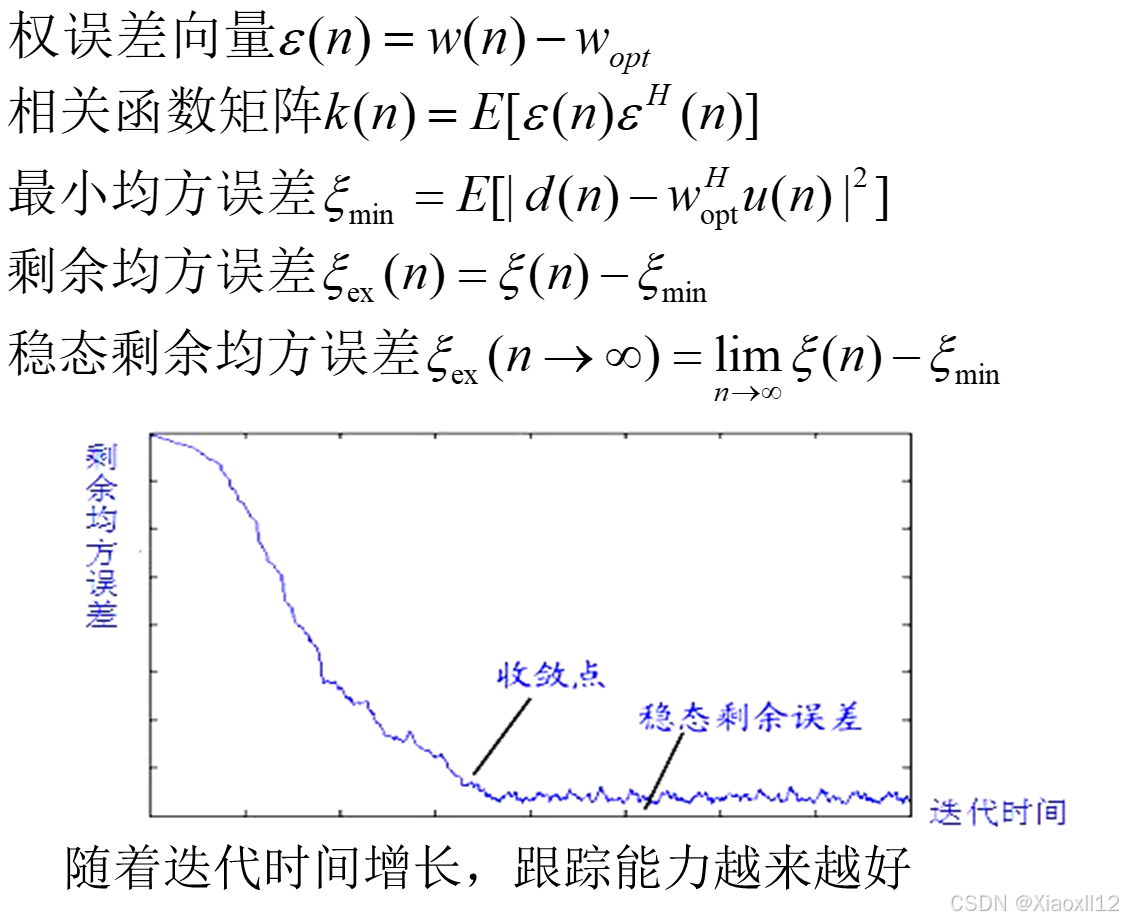
性能分析

RLS算法的快速收敛能力和高精度源于其对权重向量的精确调整。通过求解代价函数对权重向量的偏导数并置零，我们得到了一个最优权重向量的闭式解。此外，算法中的遗忘因子λ允许用户控制历史数据的权重衰减率，进一步提升了算法的灵活性和适应性。

RLS算法的特点

• 非平稳信号适应性：由于其对历史数据的加权处理，RLS算法特别适合于处理随时间变化的信号。
• 快速收敛和高精度：相较于其他自适应算法，RLS通常能在较少的迭代次数下达到更小的均方误差。
• 遗忘因子的影响：λ的选择至关重要，较大的λ意味着较长的记忆，但可能降低对信号变化的敏感性。
• 计算复杂度：虽然RLS算法提供了出色的性能，但其计算成本相对较高，可能限制了在资源受限环境下的实时应用。

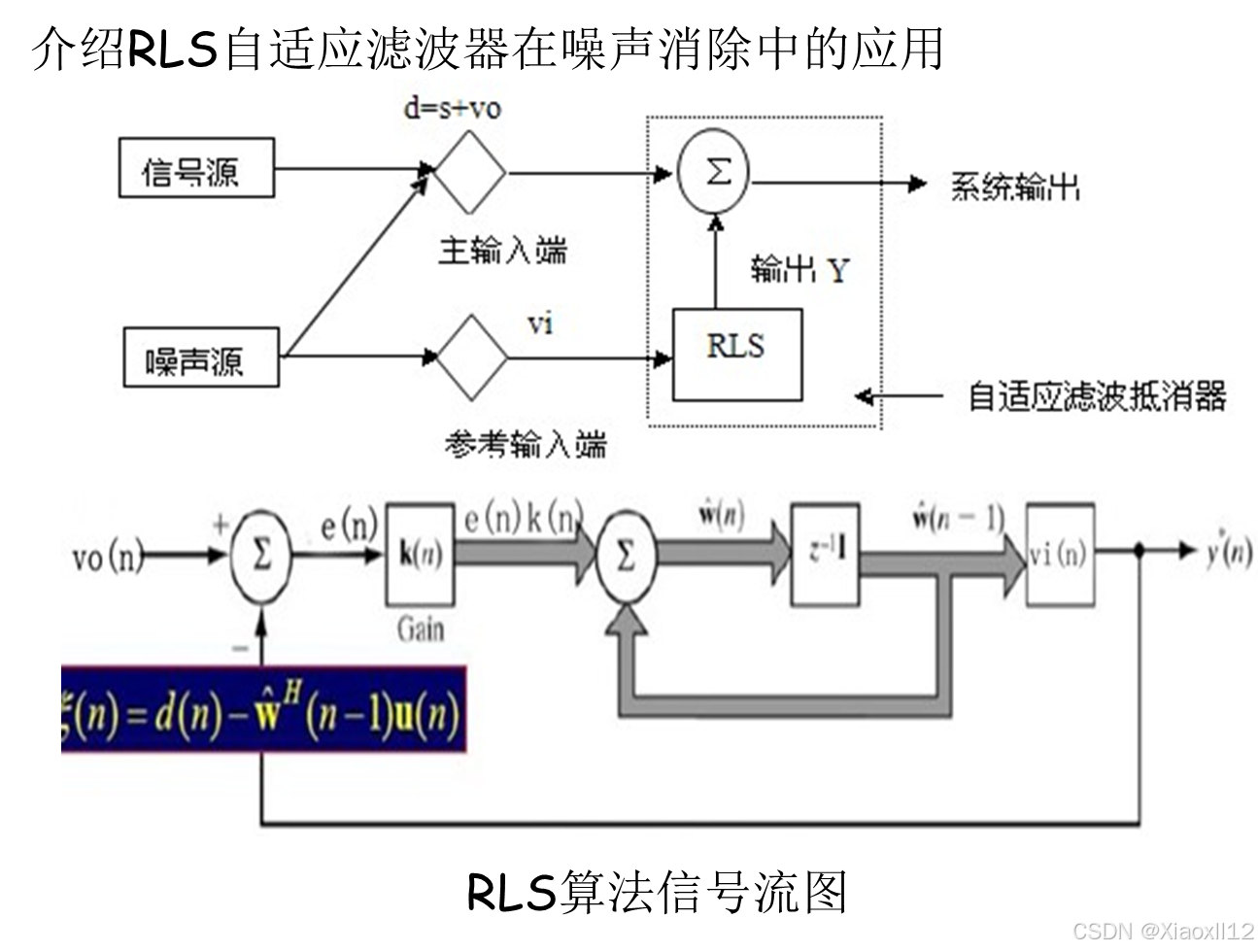
RLS算法简单应用

RLS自适应滤波器的一个典型应用是在噪声消除场景中。通过不断调整滤波器的参数，RLS能够有效抑制背景噪声，提高目标信号的质量。例如，在语音通信系统中，RLS算法可以用于去除回声和背景噪音，改善通话清晰度。

结论

RLS算法凭借其强大的自适应性和鲁棒性，在各种信号处理任务中扮演着重要角色。尽管其计算需求较高，但在许多需要高速和准确度的应用中，RLS仍然是首选的解决方案。通过理解和掌握RLS算法的工作原理，我们可以更好地将其应用于实际问题，推动信号处理技术的发展。