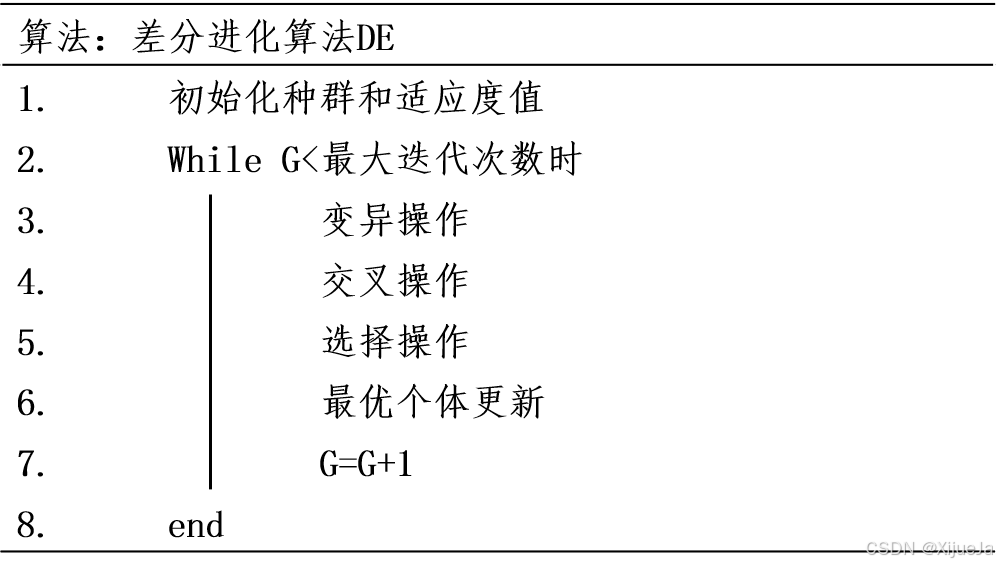​

概念与基本原理

差分进化算法（Differential Evolution，简称DE）是一种基于种群的随机优化算法，由Storm和Price在1995年提出。它主要应用于解决非线性、非凸、连续和离散的优化问题。DE算法以其简单性、鲁棒性和高效性而受到广泛关注。

差分进化算法的基本思想是通过模拟自然进化过程中的遗传和变异机制来寻找问题的最优解，类似于遗传算法。通过变异、交叉与选择，使得初始化的种群不断朝最优解的方向收敛，最终来逼近最优解。它的主要步骤包括：1.种群初始化；2.种群个体变异；3.种群个体交叉；4.种群个体选择；5.迭代直至满足条件。

算法步骤

下面将对差分进化算法的主要步骤进行详细分析。

1.种群初始化

进化种群的初始化是任何一个进化算法都必需的步骤，事实上，种群的初始化会对迭代优化求解的结果起至关重要的作用。

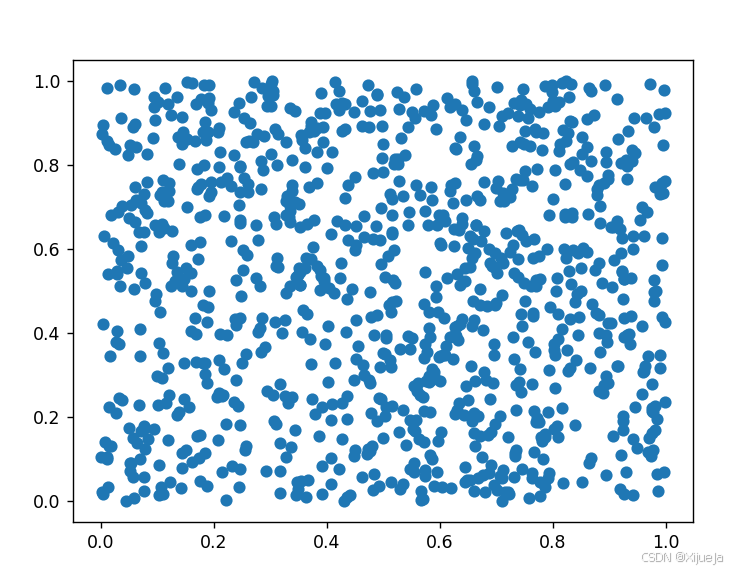
一般情况下，采用随机初始化的方式来初始化种群。以二维决策变量$x\in {\mathbb{R}}^2$为例，其中，$x$的定义域为 { ( x 1 , x 2 ) ∣ a 1 ≤ x 1 ≤ b 1 , a 2 ≤ x 2 ≤ b 2 ) } \left \{ (x_1,x_2)|a_1\leq x_1\leq b_1,a_2\leq x_2\leq b_2) \right \} {(x1​,x2​)∣a1​≤x1​≤b1​,a2​≤x2​≤b2​)}。种群大小$P_{size}$为$N$，种群$Pop$可表示为$Pop=\left\{x^{(1)},x^{(2)},...,x^{(N)}\right\}$,即$N$个二维个体的集合，此时，随机初始化的种群在二维空间呈现如图1的分布。可以看出，随机初始化会将种群个体均匀的散落在搜索空间内，这种初始化方式在应对不同的优化问题上具有很强的鲁棒性。

2.变异

变异策略是差分进化算法所有操作中最重要的一个环节之一。利用变异策略，种群可引入新个体，以此保证其多样性。一个好的变异策略应当能在保证种群多样性的同时引导种群向最优点方向收敛。目前差分进化算法中常见的变异策略包括：DE/rand/1，DE/rand/2，DE/best/1，DE/best/2和DE/current-to-best/1等。

1.DE/rand/1
该变异策略公式如下：
$$v_{i,G}=x_{r_1,G}+F\times (x_{r_2,G}-x_{r_3,G})$$
其中，$v_{i,G}$代表第G代中第个变异体，$x_{r_1,G}$,$x_{r_2,G}$,$x_{r_3,G}$代表第G代中，种群中随机挑选出的三个个体。其中，DE/rand/1中的rand指的是随机变异，即参考个体$x_{r_1,G}$,是随机选择的；1指的是有一个差分向量，即$x_{r_2,G}-x_{r_3,G}$。

2.DE/rand/2
该变异策略公式如下：
$$v_{i,G}=x_{r_1,G}+F\times (x_{r_2,G}-x_{r_3,G})+F\times (x_{r_4,G}-x_{r_5,G})$$
变量表示同DE/rand/1，不同的是，该策略从种群中随机选择了5个个体，组成了两个差分向量：$x_{r_2,G}-x_{r_3,G}$和$x_{r_4,G}-x_{r_5,G}$。

3.DE/best/1
该策略变异公式如下：
$$v_{i,G}=x_{best,G}+F\times (x_{r_1,G}-x_{r_2,G})$$
其中，$x_{best,G}$代表第G代的最优个体，$x_{r_1,G}$和$x_{r_1,G}$代表第G代中种群中随机挑选出的两个个体。DE/best/1中的best即代表参考向量为当前最优个体，1代表有一个差分向量$x_{r_1,G}-x_{r_2,G}$。

4.DE/best/2:
该策略变异公式如下：
$v_{i,G}=x_{best,G}+F\times (x_{r_1,G}-x_{r_2,G})+F\times (x_{r_3,G}-x_{r_4,G})$
其中，$x_{best,G}$代表第G代的最优个体，$x_{r_1,G}$ ,$x_{r_2,G}$, $x_{r_1,G}$,$x_{r_4,G}$代表第G代中种群中随机挑选出的四个个体。DE/best/2中的best即代表参考向量为当前最优个体，2代表有两个个差分向量$x_{r_1,G}-x_{r_2,G}$和$x_{r_3,G}-x_{r_4,G}$。
5.DE/current-to-best/1:
该策略变异公式如下：
$$v_{i,G}=x_{i,G}+F\times (x_{best,G}-x_{i,G})+F\times (x_{r_1,G}-x_{r_2,G})$$
其中，$x_{i,G}$代表第$G$代的第$i$个个体，$x_{best,G}$代表第G代的最优个体，$x_{r_1,G}$ ,$x_{r_2,G}$代表随机挑选的两个个体。DE/current-to-best/1中的current代表当前个体$x_{i,G}$，current-to-best则代表由当前个体$x_{i,G}$往最优个体$x_{best,G}$方向变异，1代表有一个差分变量$x_{r_1,G}-x_{r_2,G}$。
6.DE/rand-to-best/1:
该策略变异公式如下：
$$v_{i,G}=x_{r_1,G}+F\times (x_{best,G}-x_{r_1,G})+F\times (x_{r_2,G}-x_{r_3,G})$$
其中，$x_{r_1,G}$代表随机挑选的一个个体，$x_{best,G}$代表第G代的最优个体，$x_{r_2,G}$ ,$x_{r_3,G}$代表随机挑选的另外两个个体。DE/rand-to-best/1中的rand代表随机个体$x_{r_1,G}$，rand-to-best则代表由当前个体$x_{r_1,G}$往最优个体$x_{best,G}$方向变异，1代表有一个差分变量$x_{r_2,G}-x_{r_3,G}$。

在上述变异策略中，存在一个超参数F，该参数被称为变异因子F，实验与研究表明，该参数对差分进化的搜索效果有极其重要的作用，进而衍生出了许多关于F参数自适应更新的策略。

3.交叉

交叉操作发生在父代个体$x_{i,G}$与子代个体$v_{i,G}$之间，目前最常用的交叉方式如下：
$$u_{j,i,G}=\{\begin{array}{rlrl}{v}_{j,i,G}& & rand[0,1]\le CR或j=j_{rand}& \\ x_{j,i,G}& & 否则& \end{array}$$
其中，$u_{j,i,G}$代表第$G$代交叉操作后，第$i$个个体在第$j$个维度上的值。CR为交叉因子，是差分进化算法中除了变异因子F外最重要的另一个超参数。该交叉操作的原理如下：对第$i$对子代(变异)个体与父代(原)个体,遍历它们的每一维度$j$，并随机生成一个0到1的随机数，如果该随机数小于CR，则交叉后得到的$u_{j,i,G}$为$v_{j,i,G}$，否则，保持为$x_{j,i,G}$。同时，为避免交叉操作的概率较低，还会随机选择一个维度$j_{rand}$，强制性地使该维度进行交叉操作。最终，得到交叉后的个体$u_{i,G}$。

4.选择

选择操作则是发生在交叉个体$u_{i,G}$与原个体$x_{i,G}$之间。由前面操作可知，$u_{i,G}$包含了变异与交叉所生成的信息，通过比较每一对$u_{i,G}$与$x_{i,G}$的好坏，来保留下适应度更优的个体：
$$x_{i,G+1}=\{\begin{array}{rlr}{u}_{i,G}& & 如果f(u_{i,G})\le f(x_{i,G})\\ x_{i,G}& & 否则\end{array}$$
如果交叉后的个体$u_{i,G}$所计算的适应度函数$f(u_{i,G})$不大于$f(x_{i,G})$，则$u_{i,G}$优于$x_{i,G}$，否则，保留原个体，以此来实现种群朝着最优解不断更新的效果。

5.迭代计算

在种群初始化后，通过不断重复的变异、交叉与选择，实现种群超最优解方向进化的效果。至此，整体流程可总结如下：

总结

以上便是差分进化算法的原理介绍。研究表明，DE算法的效果主要取决于算法参数的设置，包括变异因子F，交叉参数CR，种群大小等。目前有许多针对参数设定的自适应方法，由此出现了许多经典的DE变体算法，例如SADE、JADE、SHADE和L-SHADE等等，后续我们将分别介绍以上算法。
最后附上DE算法的Python代码，通过更改适应度函数可直接使用。

Python代码

import numpy as np
class DE():
    '''
    DE算法
    输入：   fitness:适应度函数
            constraints:约束条件
            lowwer:下界
            upper:上界
            pop_size:种群大小
            dim:维度
            mut_way:变异方式
            epochs:迭代次数
    输出：   best:最优个体
    '''
    def __init__(self,fitness,constraints,lowwer,upper,pop_size,dim,mut_way,epochs):
        self.fitness=fitness#适应度函数
        self.constraints=constraints#约束条件
        self.lowbound=lowwer#下界
        self.upbound=upper#上界
        self.pop_size=pop_size#种群大小
        self.dim=dim#种群大小
        self.population=np.random.rand(self.pop_size,self.dim)#种群
        self.fit=np.random.rand(self.pop_size)#适应度
        self.mut_way=mut_way
        self.best=self.population[0]#最优个体
        self.F=0.5#缩放因子
        self.CR=0.1#交叉概率
        self.Epochs=epochs#迭代次数
        self.NFE=0#函数评价次数
    '''种群初始化'''
    def initpop(self):
        self.population = self.lowbound + (self.upbound - self.lowbound) * np.random.rand(self.pop_size,self.dim)  # 种群初始化
        self.fit = np.array([self.fitness(chrom) for chrom in self.population])  # 适应度初始化,此处复杂度为pop_size
        self.NFE += self.pop_size#更新函数评价次数
        self.best = self.population[np.argmin(self.fit)]  # 最优个体初始化

    '''变异'''
    def mut(self):
        mut_population = []#定义新种群
        if self.mut_way=='DE/rand/1':
            for i in range(self.pop_size):
                # 随机选择三个不同于当前个体的个体
                idxs = np.random.choice(np.delete(np.arange(self.pop_size), i), 3, replace=False)
                a, b, c = self.population[idxs]
                # print(idxs)
                v=a+self.F*(b-c)#突变运算
                mut_population.append(v)
        elif self.mut_way=='DE/best/1':
            for i in range(self.pop_size):
                # 随机选择二个不同于当前个体的个体
                idxs = np.random.choice(np.delete(np.arange(self.pop_size), i), 2, replace=False)
                a, b = self.population[idxs]
                v=self.best+self.F*(a-b)#突变运算
                mut_population.append(v)
        elif self.mut_way=='DE/rand/2':
            for i in range(self.pop_size):
                # 随机选择五个不同于当前个体的个体
                idxs = np.random.choice(np.delete(np.arange(self.pop_size), i), 5, replace=False)
                a, b, c,d,e = self.population[idxs]
                v=a+self.F*(b-c)+self.F*(d-e)#突变运算
                mut_population.append(v)
        elif self.mut_way=='DE/best/2':
            for i in range(self.pop_size):
                # 随机选择四个不同于当前个体的个体
                idxs = np.random.choice(np.delete(np.arange(self.pop_size), i), 4, replace=False)
                a, b, c,d = self.population[idxs]
                v=self.best+self.F*(a-b)+self.F*(c-d)
                mut_population.append(v)
        elif self.mut_way=='DE/current-to-best/1':
            for i in range(self.pop_size):
                # 随机选择三个不同于当前个体的个体
                idxs = np.random.choice(np.delete(np.arange(self.pop_size), i), 3, replace=False)
                a, b, c = self.population[idxs]
                v=self.population[i]+self.F*(self.best-self.population[i])+self.F*(a-b)
                mut_population.append(v)
        return mut_population

    '''交叉'''
    def cross(self,mut_population):
        cross_population=self.population.copy()
        for i in range(self.pop_size):
            j=np.random.randint(0,self.dim)#随机选择一个维度
            for k in range(self.dim):#对每个维度进行交叉
                if np.random.rand()<self.CR or k==j:#如果随机数小于交叉率或者维度为j
                    cross_population[i][k]=mut_population[i][k]#交叉
        return cross_population
    '''选择'''
    def select(self,cross_population):
        for i in range(self.pop_size):#比较每一个个体的适应度
            temp=self.fitness(cross_population[i])#计算适应度
            self.NFE+=1#更新函数评价次数
            if temp<self.fit[i]:#如果新适应度更好
                self.fit[i]=temp#更新适应度
                self.population[i]=cross_population[i]#更新个体

    '''迭代搜索'''
    def run(self):
        self.initpop()#初始化种群
        for i in range(self.Epochs):#迭代
            mut_population=self.mut()#变异
            cross_population=self.cross(mut_population)#交叉
            self.select(cross_population)#选择
            self.best=self.population[np.argmin(self.fit)]#更新最优个体
            # 打印每次迭代的种群最优值，均值，最差值，方差
            print('epoch:', i, 'best:', np.min(self.fit),
                  'mean:', np.mean(self.fit),
                  'worst:', np.max(self.fit),
                  'std:', np.std(self.fit))
        return self.best#返回最优个体

if __name__ == '__main__':
    '''测试用例'''
    def fitness(x):#目标函数，仅需修改此处
        return np.sum(x**2)
    def constraints(x):
        return 0

    lowwer=-10#决策变量下界
    upper=10#决策变量上界
    pop_size=100#种群大小
    dim=2#决策变量维度
    mut_way='DE/rand/1'#变异方式
    epochs=50#迭代次数
    de=DE(fitness,constraints,lowwer,upper,pop_size,dim,mut_way,epochs)
    best=de.run()

    print("最优解：x=",best)
    print("最优值：f(x)=",fitness(best))

​