💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
文献1:
本文研究了一般有向图下具有一般线性动态的多智能体系统的事件触发共识问题。基于状态反馈,我们为每个智能体提出了一种分布式事件触发共识控制器(ETCC),以实现共识,而无需智能体之间进行连续通信。每个智能体只需持续监测自身的状态,以确定何时触发事件并将其状态广播给其出邻居节点。当智能体向其出邻居广播状态或从入邻居节点接收新信息时,会更新其控制器。ETCC可以分多步实现。证明了在所提出的ETCC下,系统不会出现Zeno行为。为了降低对每个智能体自身状态持续监测的要求,我们进一步提出了一种自触发共识控制器(STCC)。通过仿真结果验证了理论分析,并展示了本文提出的事件触发和自触发控制器的优势。
文献2:
摘要——本文研究了一般有向图下具有一般线性动态的多智能体系统的事件触发共识问题。我们为每个智能体提出了一种分布式事件触发共识控制器(ETCC),以实现共识,而无需智能体之间进行连续通信。每个智能体只需持续监测自身的状态,以确定何时触发事件并将其状态广播给其出邻居节点。当智能体向其出邻居广播状态或从入邻居节点接收新信息时,会更新其控制器。ETCC可以分多步实现。我们证明了在所提出的ETCC下,系统不会出现Zeno行为。为了降低对每个智能体自身状态持续监测的要求,我们进一步提出了一种自触发共识控制器(STCC)。通过仿真结果验证了理论分析,并展示了本文提出的事件触发和自触发控制器的优势。
关键词——分布式事件触发,共识控制,多智能体系统,一般线性动态,有向图。
摘要
近年来,多智能体系统(MAS)因其广泛的应用而受到广泛关注。许多重要的研究成果已经取得,例如[1]–[6],这里仅举几例。需要注意的是,在上述研究中,智能体需要持续使用自身和邻居的状态信息,因此这些状态信息需要不断获取。为了避免这一缺点,一些研究人员开始研究集中式/分布式事件触发共识问题[7]–[14]。对于具有单积分器动态的多智能体系统,事件触发平均共识问题在[7]和[8]中进行了研究。具有一般线性动态的多智能体系统的事件触发共识问题在[10]和[15]中进行了探讨。然而,尽管[7]、[8]、[10]和[15]中的控制器通过使用事件触发算法减少了更新频率,但它们仍然需要智能体与邻居持续通信。
众所周知,不必要的通信会导致能量浪费。持续通信还会导致智能体之间的通信资源竞争。为了尽可能减少通信成本,研究人员最近开始研究无需持续通信的事件触发共识、自触发共识或分布式事件触发共识[9]、[11]–[14],其中无需持续通信。[9]研究了基于周期性事件触发的单积分器智能体在无向连通通信拓扑下的共识算法。[11]给出了单积分器智能体的自触发控制算法。[12]研究了单积分器和双积分器智能体的分布式事件触发共识算法。然而,在[9]、[11]和[12]中,智能体被假设为具有单积分器或双积分器动态。对于具有一般线性动态的多智能体系统,尽管[13]、[14]和[15]最近解决了无需持续通信的事件触发共识问题,但它们都存在一些限制。[13]中的共识误差只能收敛到原点周围的邻域,而[14]和[15]中的通信拓扑被假设为无向的。简而言之,具有一般线性动态的多智能体系统在有向图下的事件触发共识问题尚未得到解决。
受上述讨论的启发,我们基于事件触发广播方案,研究了一般有向图下具有一般线性动态的多智能体系统的共识问题。假设智能体之间的通信拓扑是一个包含有向生成树的一般有向图。我们为每个智能体提出了一种分多步实现的分布式事件触发共识控制器(ETCC),以实现共识。在我们提出的控制器下,智能体之间无需持续通信。我们进一步证明了在控制过程中不会出现Zeno行为,即事件不会持续触发。需要注意的是,在ETCC下,每个智能体需要持续监测自身的状态。为了放宽这一限制,我们进一步提出了一种自触发共识控制器(STCC),智能体在上一次触发时刻预设下一次触发时刻。需要指出的是,闭环系统的稳定性分析部分受到[5]和[12]的启发。本文的主要贡献总结如下:
-
据我们所知,这是第一篇在无需持续通信和监测的情况下,针对具有一般线性动态的多智能体系统在一般有向图下研究事件触发/自触发共识问题的论文。现有文献中的大多数研究存在一些限制,例如智能体动态、通信图、非零最终共识误差和持续通信等。因此,文献中的方法不能直接应用于本文。
-
在提出的ETCC中使用了矩阵指数函数e^(At),以估计智能体的当前状态并排除Zeno行为。需要注意的是,对于单积分器智能体,基于事件的控制器可以直接从连续共识控制器中获得。但对于双积分器智能体或一般线性智能体,连续控制器不能直接以事件触发的形式实现。引入矩阵指数函数e^(At)是我们的研究的一个创新点。[12]中处理单积分器和双积分器动态的结果可以视为我们结果的一个特例。需要指出的是,在我们的框架中,收敛性分析和排除Zeno行为的分析并非微不足道,存在显著挑战。
本文的其余部分安排如下:第II节介绍一些有用的结果和动态;第III节研究事件触发共识;第IV节讨论自触发方案;第V节给出仿真例子;第VI节总结本文。
📚2 运行结果
部分代码:
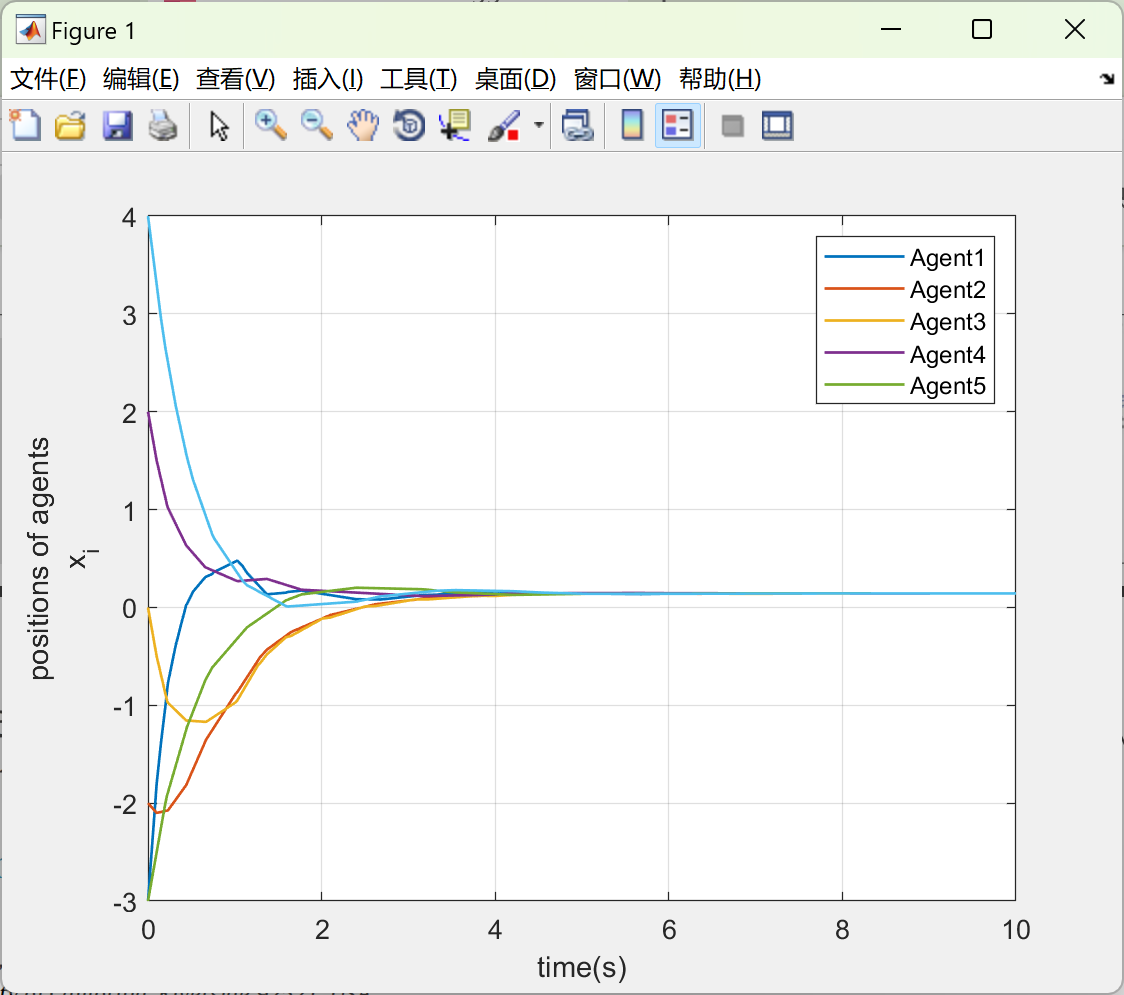
figure(1)
plot(Ts,x1,'LineWidth',1);
xlabel('time(s)');ylabel({'positions of agents';'x_{i}'});
legend('Agent1','Agent2','Agent3','Agent4','Agent5')
grid on
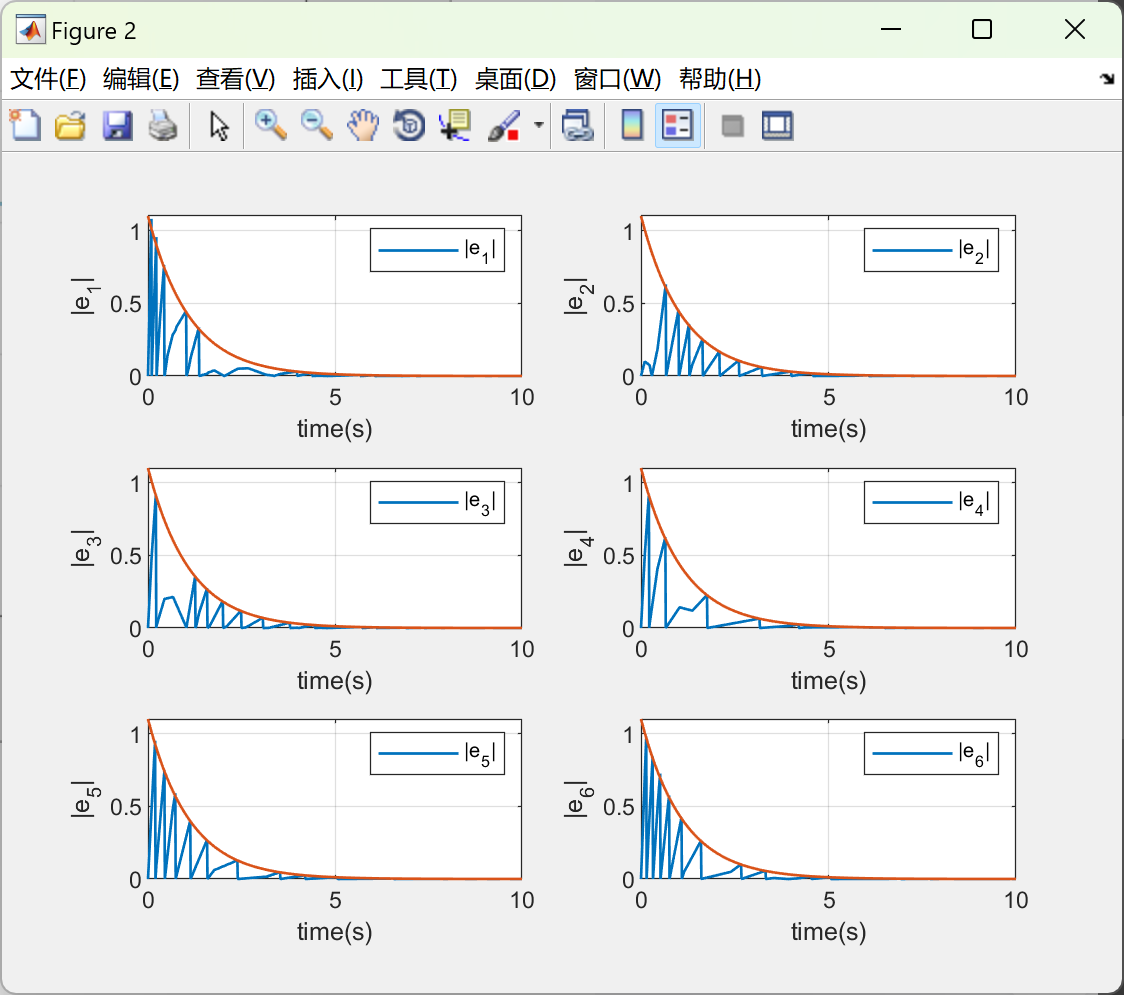
figure(2)
subplot(3, 2, 1);
plot(Ts,abs(E(:,1)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{1}|');
legend('|e_{1}|')
grid on
subplot(3, 2, 2);
plot(Ts,abs(E(:,2)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{2}|');
legend('|e_{2}|')
grid on
subplot(3, 2, 3);
plot(Ts,abs(E(:,3)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{3}|');
legend('|e_{3}|')
grid on
subplot(3, 2, 4);
plot(Ts,abs(E(:,4)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{4}|');
legend('|e_{4}|')
grid on
subplot(3, 2, 5);
plot(Ts,abs(E(:,5)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{5}|');
legend('|e_{5}|')
grid on
subplot(3, 2, 6);
plot(Ts,abs(E(:,6)),Ts,line1,'LineWidth',1);
xlabel('time(s)');ylabel('|e_{6}|');
legend('|e_{6}|')
grid on
figure(3)
plot(Ts,U,'LineWidth',1);
xlabel('time(s)');ylabel('control input');
legend('Agent1','Agent2','Agent3','Agent4','Agent5')
grid on
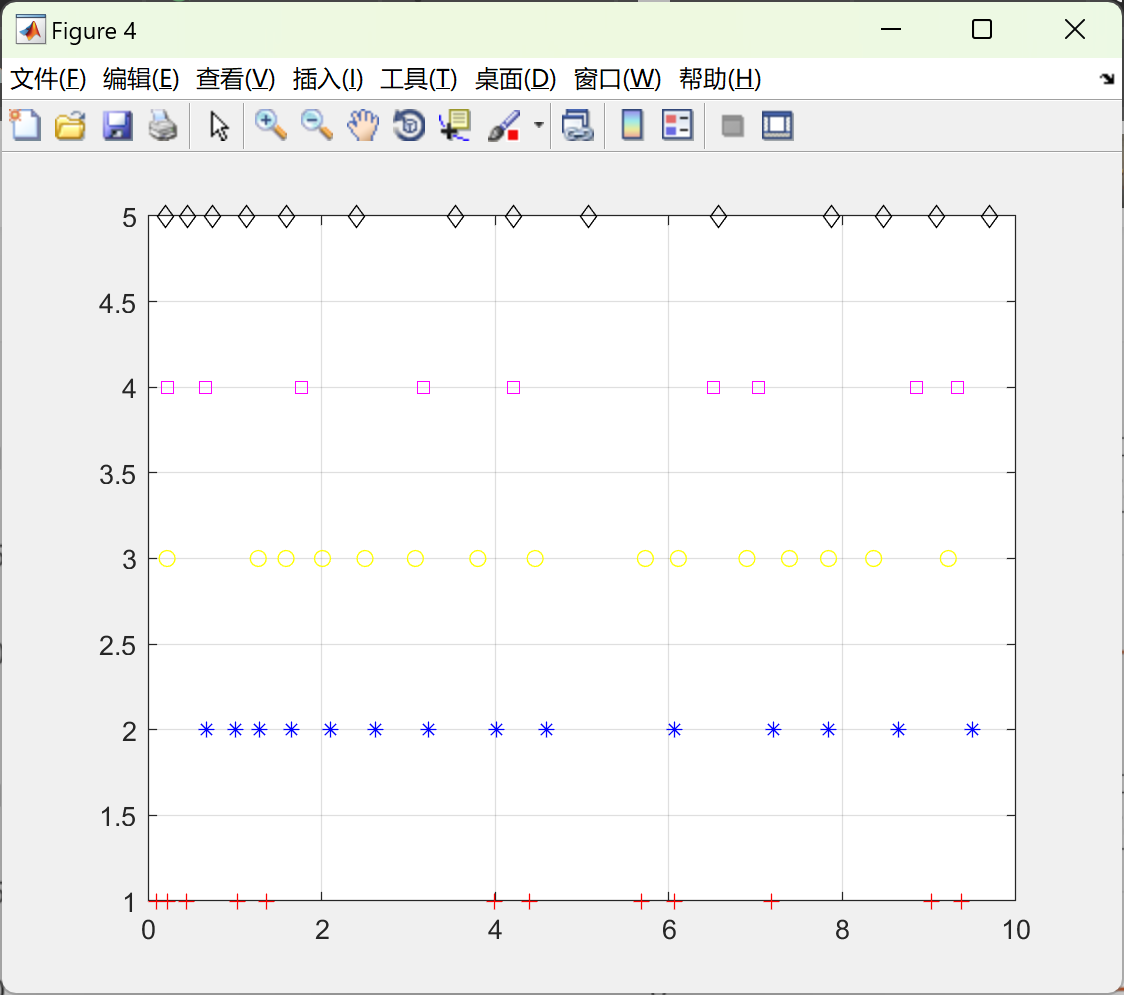
figure(4)
plot(T1,B1,'+r',T2,B2,'*b',T3,B3,'oy',T4,B4,'squarem',T5,B5,'diamondk');
grid on
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
🌈4 Matlab代码、两篇文献下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取