Dijkstra算法图文详解

Dijkstra算法是路径规划算法中非常经典的一种算法，在很多地方都会用到，特别是在机器人的路径规划中，基本学习机器人运动相关的都会接触到该算法。Dijkstra算法本身的原理是基于贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

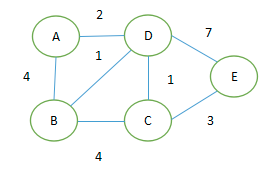
这样一个有权图，Dijkstra算法可以计算任意节点到其他节点的最短路径
在这里插入图片描述

算法思路

1.指定一个节点，例如我们要计算 ‘A’ 到其他节点的最短路径

2.引入两个集合（S、U），S集合包含已求出的最短路径的点（以及相应的最短长度），U集合包含未求出最短路径的点（以及A到该点的路径，注意如上图所示，A->C由于没有直接相连初始时为∞）

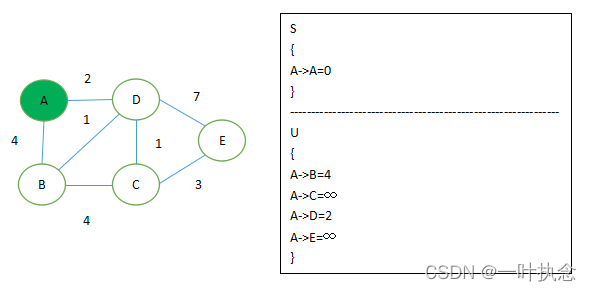
3.初始化两个集合，S集合初始时只有当前要计算的节点，A->A = 0，U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞，敲黑板！！！接下来要进行核心两步骤了

4.从U集合中找出路径最短的点，加入S集合，例如 A->D = 2

5.更新U集合路径，if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 则更新U

6.循环执行 4、5 两步骤，直至遍历结束，得到A 到其他节点的最短路径

算法图解

1.选定A节点并初始化，如上述步骤3所示
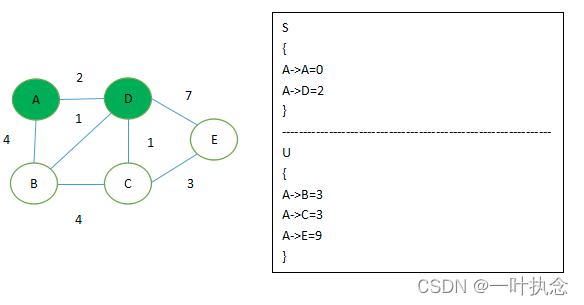
在这里插入图片描述
2.执行上述 4、5两步骤，找出U集合中路径最短的节点D 加入S集合，并根据条件 if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 来更新U集合

3.这时候 A->B, A->C 都为3，没关系。其实这时候他俩都是最短距离，如果从算法逻辑来讲的话，会先取到B点。而这个时候 if 条件变成了 if ( ‘B 到 C,E 的距离’ + ‘AB 距离’ < ‘A 到 C,E 的距离’ ) ，如图所示这时候A->B距离其实为 A->D->B

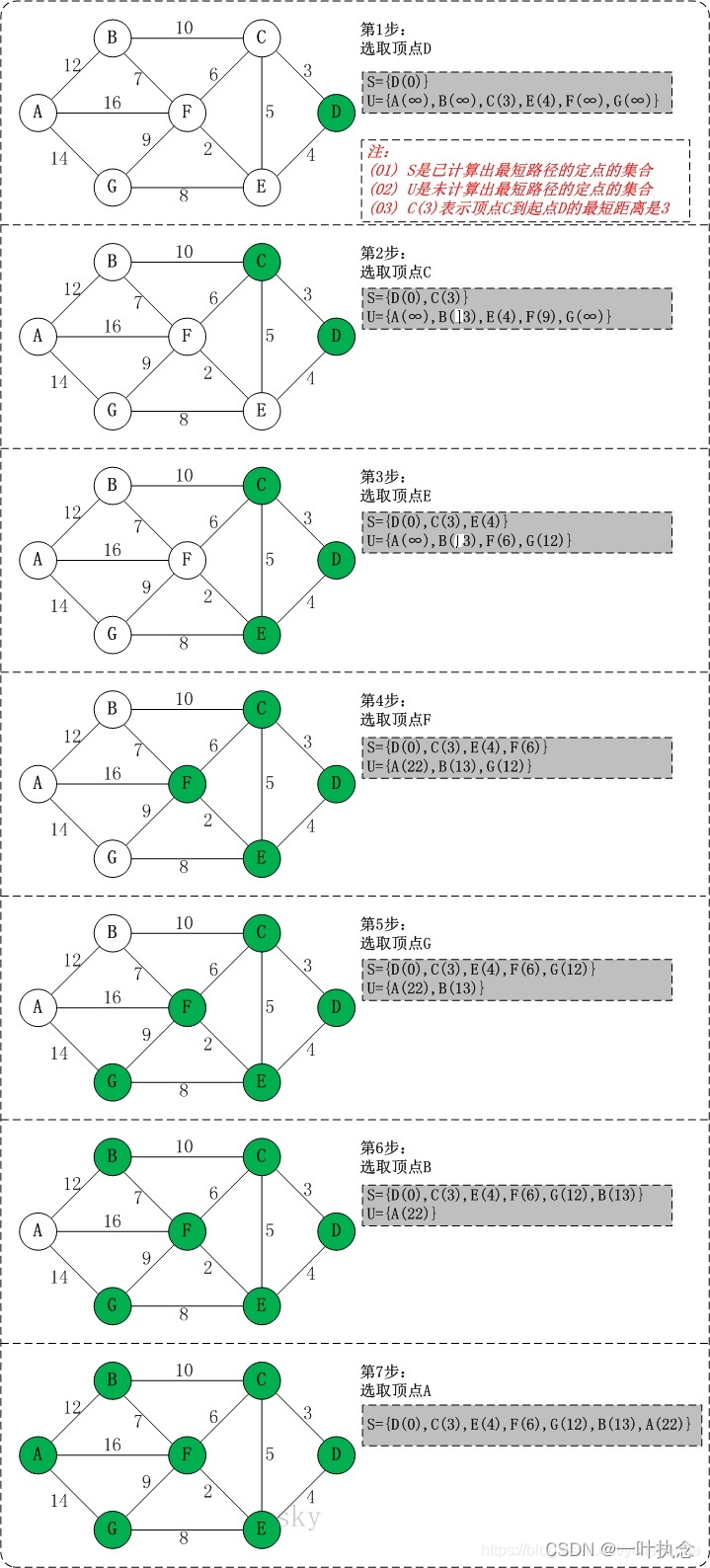
例二.这个图表示的也非常清楚。
(以第4个顶点D为起点)
在这里插入图片描述
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！
第1步：将顶点D加入到S中。
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, U={A(∞),B(13),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, U={A(∞),B(13),F(6),G(12)}。

第4步：将顶点F加入到S中。
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

Dijkstra算法与路径规划

Dijkstra算法是很有代表性的最短路径规划算法。一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用OPEN, CLOSE表方式，路径规划采用OPEN,CLOSE表的方式。

大概过程：
创建两个表，OPEN, CLOSE。
OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。
1．访问路网中里起始点最近且没有被检查过的点，把这个点放入OPEN组中等待检查。
2．从OPEN表中找出距起始点最近的点，找出这个点的所有子节点，把这个点放到CLOSE表中。
3．遍历考察这个点的子节点。求出这些子节点距起始点的距离值，放子节点到OPEN表中。
4．重复2，3，步。直到OPEN表为空，或找到目标点。

代码实现:

import os
import sys
import math
import heapq

sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
                "/../../Search_based_Planning/")

from Search_2D import plotting, env




class Dijkstra:
    """Dijkstra set the cost as the priority 
    """
    def __init__(self, s_start, s_goal, heuristic_type):
        self.s_start = s_start
        self.s_goal = s_goal
        self.heuristic_type = heuristic_type

        self.Env = env.Env()  # class Env

        self.u_set = self.Env.motions  # feasible input set
        self.obs = self.Env.obs  # position of obstacles

        self.OPEN = []  # priority queue / OPEN set
        self.CLOSED = []  # CLOSED set / VISITED order
        self.PARENT = dict()  # recorded parent
        self.g = dict()  # cost to come
    def get_neighbor(self, s):
        """
        find neighbors of state s that not in obstacles.
        :param s: state
        :return: neighbors
        """
        #print([(s[0] + u[0], s[1] + u[1]) for u in self.u_set])
        #print("__________")
        return [(s[0] + u[0], s[1] + u[1]) for u in self.u_set]

    def cost(self, s_start, s_goal):
        """
        Calculate Cost for this motion
        :param s_start: starting node
        :param s_goal: end node
        :return:  Cost for this motion
        :note: Cost function could be more complicate!
        """

        if self.is_collision(s_start, s_goal):
            return math.inf

        return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])
    def is_collision(self, s_start, s_end):
        """
        check if the line segment (s_start, s_end) is collision.
        :param s_start: start node
        :param s_end: end node
        :return: True: is collision / False: not collision
        """

        if s_start in self.obs or s_end in self.obs:
            return True

        if s_start[0] != s_end[0] and s_start[1] != s_end[1]:
            if s_end[0] - s_start[0] == s_start[1] - s_end[1]:
                s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
                s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
            else:
                s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
                s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))

            if s1 in self.obs or s2 in self.obs:
                return True

        return False
    def extract_path(self, PARENT):
        """
        Extract the path based on the PARENT set.
        :return: The planning path
        """

        path = [self.s_goal]
        s = self.s_goal

        while True:
            s = PARENT[s]
            path.append(s)

            if s == self.s_start:
                break

        return list(path)

    def searching(self):
        """
        Breadth-first Searching.
        :return: path, visited order
        """

        self.PARENT[self.s_start] = self.s_start
        self.g[self.s_start] = 0
        self.g[self.s_goal] = math.inf
        heapq.heappush(self.OPEN,
                       (0, self.s_start))

        while self.OPEN:
            _, s = heapq.heappop(self.OPEN)
            self.CLOSED.append(s)

            if s == self.s_goal:
                break
            #print(s)
            for s_n in self.get_neighbor(s):
                #print(s_n)
                new_cost = self.g[s] + self.cost(s, s_n)

                if s_n not in self.g:
                    self.g[s_n] = math.inf

                if new_cost < self.g[s_n]:  # conditions for updating Cost
                    self.g[s_n] = new_cost
                    self.PARENT[s_n] = s
                    print(s_n)
                    print(s)
                    print("__________")
                    # best first set the heuristics as the priority 
                    heapq.heappush(self.OPEN, (new_cost, s_n))
            #print(self.g[s])
        return self.extract_path(self.PARENT), self.CLOSED


def main():
    s_start = (38, 24)
    s_goal = (45, 25)

    dijkstra = Dijkstra(s_start, s_goal, 'None')
    plot = plotting.Plotting(s_start, s_goal)

    path, visited = dijkstra.searching()
    plot.animation(path, visited, "Dijkstra's")  # animation generate


if __name__ == '__main__':
    main()

这个代码是来自于博客《路径规划算法》，简单做了点改动，方便理解。

算法的思路主要注意以下几点：

1、首先，在初始状态下，除了起点的代价值为0外，其他位置的代价值都为无穷大。
2、其次，每个点的代价值运算遵从以下原则：

g[0,s+1] = g[0,s]+g[s,s+1]

在这样的两个原则下，Dijkstra算法就可以从已知环境中找到一条全局路径。它的思路主要分为以下几步：

1、将起点的cost值设置为0，起点以外的点的cost值设置为无穷大。
2、从起点开始遍历与当前点相邻的点，计算它们的cost值，如果比无穷大要小则更新为当前的cost值。
注意这里是一个循环，它当中维护了两个字典：
第一个用于保存每个点的cost值，用于计算g[0,s+1] = g[0,s]+g[s,s+1]；
第二个用于保存每个点与之相邻的点的坐标，即这个点是由于搜索哪个点附近的点所进行计算的。例如对[23,7]进行搜索时，会搜索[23,6]、[23,8]、[22,7]、[24,7]四个方向的点，则这四个点的相邻点坐标都为[23,7]，即它们都是由[23,7]扩展出去的。这里很重要，用于回朔寻找路径。
3、循环执行步骤2，直到找到终点。
4、根据2中保存的第二个字典，回朔寻找出起点到终点的路径。

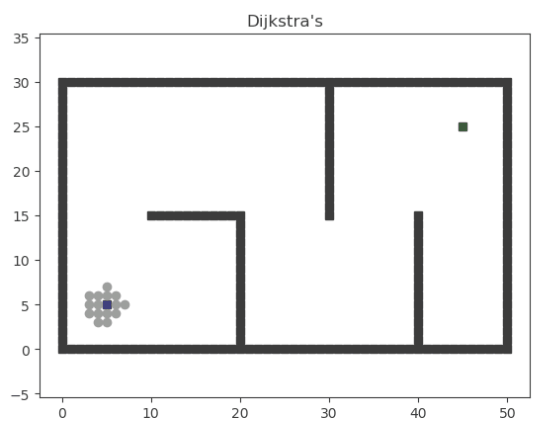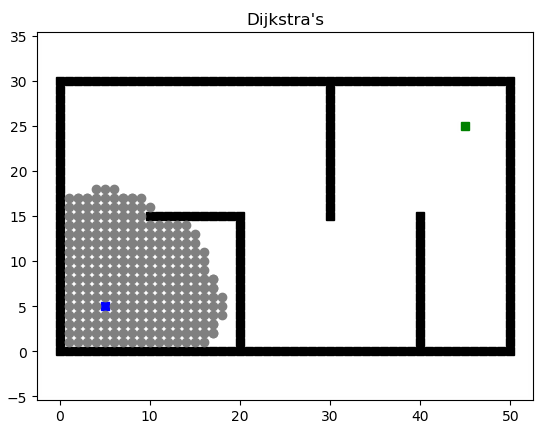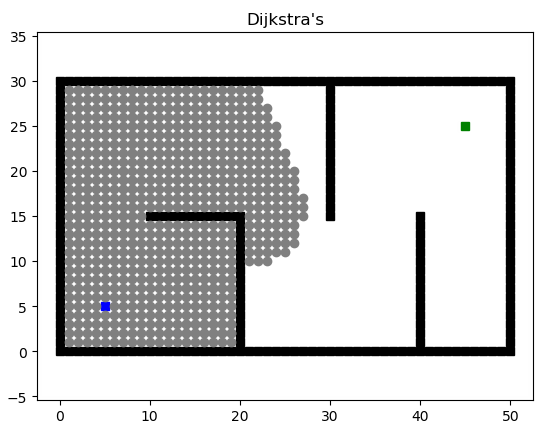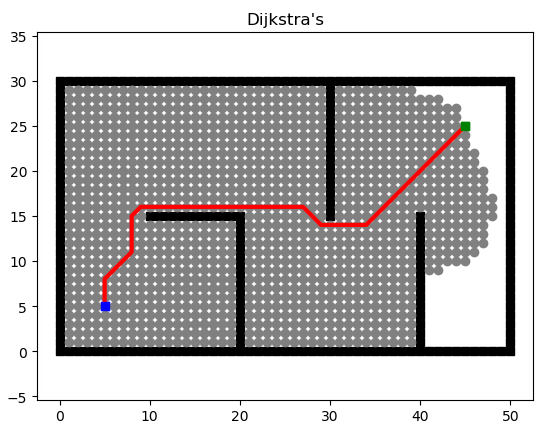
最终的效果如下：
在这里插入图片描述

参考:

https://blog.csdn.net/lbperfect123/article/details/84281300

https://blog.csdn.net/yalishadaa/article/details/55827681

https://www.cnblogs.com/guxuanqing/p/9610780.html

https://blog.csdn.net/weixin_44574633/article/details/116599738?spm=1001.2101.3001.6650.11&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-11.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-11.no_search_link