常微分方程Matlab数值解法-#3龙格—库塔法

前言

尽管改进的欧拉法相对于简单欧拉法较为精确，但是对于很多实际的问题，运用这两种方法仍然得不到足够精确的解。龙格—库塔法（ Runge-Kutta）是较之前两种方法计算精度更高的方法。

一、基本原理

在龙格—库塔法中，四阶龙格—库塔法的局部截断误差约为 o(h^5) ，被广泛应用于解微分方程的初值问题。其算法公式为：

二、使用步骤

1.四阶龙格—库塔算法的编程实现
在 MATLAB 中编程实现四阶龙格—库塔算法的函数为： MyRunge_Kutta

function [x,y] = MyRunge_Kutta(fun,x0,xt,y0,PointNum,varargin)

%用龙格—库塔法解微分方程 y%(t)=f(x,y(x))
%此程序可解高阶的微分方程。只要将其形式写为上述微分方程的向量形式
%函数 f（ x， y）： fun
%自变量的初值和终值： x0,xt
%y0 表示函数在 x0 处的值，输入初值为列向量形式
%自变量在[x0,xt]上取的点数： PointNum
%varargin 为可选输入项，可传适当参数给函数 f(x,y)
%x：所取的点的 x 值
%y：对应点上的函数值

if nargin < 4 | PointNum <= 0
PointNum= 100;
end
if nargin < 3
y0 = 0;
end
y(1,:) = y0(:)'; %初值存为行向量形式
h = (xt-x0)/(PointNum-1); %计算步长
x = x0+[0:PointNum]'*h; %得 x 向量值
for k = 1:PointNum %迭代计算
f1 = h*feval(fun,x(k),y(k,:),varargin{:});
f1 = f1(:)'; %得公式中 k1
f2 = h*feval(fun,x(k) + h/2,y(k,:) + f1/2,varargin{:});
f2 = f2(:)'; %得公式中 k2
f3 = h*feval(fun,x(k) + h/2,y(k,:) + f2/2,varargin{:});
f3 = f3(:)'; %得公式中 k3
f4 = h*feval(fun,x(k) + h,y(k,:) + f3,varargin{:});
f4 = f4(:)'; %得公式中 k4
y(k + 1,:) = y(k,:) + (f1 + 2*(f2 + f3) + f4)/6; %得 y(n+1)
end

2.计算实例

%用三种不同方法解微分方程
clear, clf %清除内存中的变量
x0=0;
xt=2;
Num=100;
h=(xt-x0)/(Num-1);
x =x0+[0:Num]*h;
a = 1;
yt = 1-exp(-a*x); %真值解
fun = inline('-y + 1','x','y'); %用 inline 构造函数 f(x,y)
y0 = 0; %设定函数初值
PointNum = 4; %设定取点数
[x1,ye] = MyEuler(fun,x0,xt,y0,PointNum);
[x2,yh] = MyEulerPro(fun,x0,xt,y0,PointNum);
[x3,yr] = MyRunge_Kutta(fun,x0,xt,y0,PointNum);
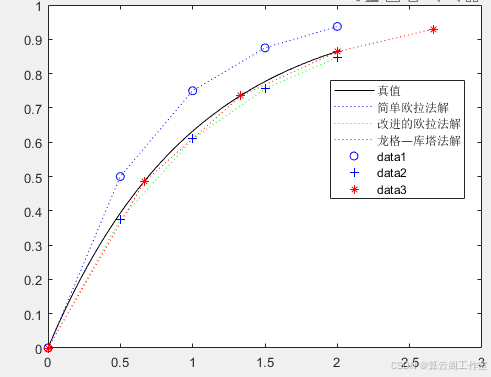
plot(x,yt,'k', x1,ye,'b:', x2,yh,'g:', x3,yr,'r:')
legend('真值','简单欧拉法解','改进的欧拉法解','龙格—库塔法解')

hold on
plot(x1,ye,'bo',x2,yh,'b+', x3,yr,'r*')
PointNum= 1000; %估计各算法运行 PointNum 步迭代的时间
tic %计时开始
[x1,ye] = MyEuler(fun,x0,xt,y0,PointNum);
time_Euler = toc %得到欧拉法的运行时间
tic
[x1,yh] = MyEulerPro(fun,x0,xt,y0,PointNum);
time_EulerPro = toc %得到改进的欧拉法运行时间
tic
[x1,yr] = MyRunge_Kutta(fun,x0,xt,y0,PointNum);
time_RK4 = toc %得到龙格—库塔法运行时间

>> ex11_4

time_Euler =

0.0750
time_EulerPro =

0.1585
time_RK4 =

0.2910

由运算结果可知，龙格—库塔法可得到与真值几乎相同的微分方程数值解。但其相应的程序运
行时间较长，几乎是简单欧拉法的4倍。

常微分方程Matlab数值解法-#3龙格—库塔法

悦读