算法导论ch12二叉搜索树中文笔记与其数据结构c++实现

算法导论ch12二叉搜索树笔记与其数据结构c++实现

算法导论ch12二叉搜索树笔记与其数据结构c++实现

算法导论ch12二叉搜索树笔记与其数据结构c++实现

作者：Claude Du

本篇笔记主要来源于算法导论第三版中文版与算法导论第四版英文版，c++代码实现有参考邓俊辉的数据结构（c++语言版）第三版，其中我自行修改了算法导论中部分描述型的错误，如果还有错误, 请各位务必指出。

搜索树数据结构支持许多动态集合操作：SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT和DELETE等。因此，我们使用一棵搜索树既可以作为一个字典又可以作为一个优先队列。

二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。对于有n节点的完全二叉树，这些操作的最坏运行时间为 $\Theta(lgn)$ 。但对于有n节点的线性链形的二叉树，这些操作的最坏运行时间为 $\Theta(n)$ 。

实际上，我们经常使用的是二叉搜索树的变种，因为它们可以保证基本操作有较好的最坏情况性能。比如13章的红黑树，18章的B树，特别适用于二级（磁盘）存储器上的数据库维护。

下文中，我将二叉搜索树简称称为BST, 即Binary Search Tree的缩写。

12.1 什么是二叉搜索树(BST)

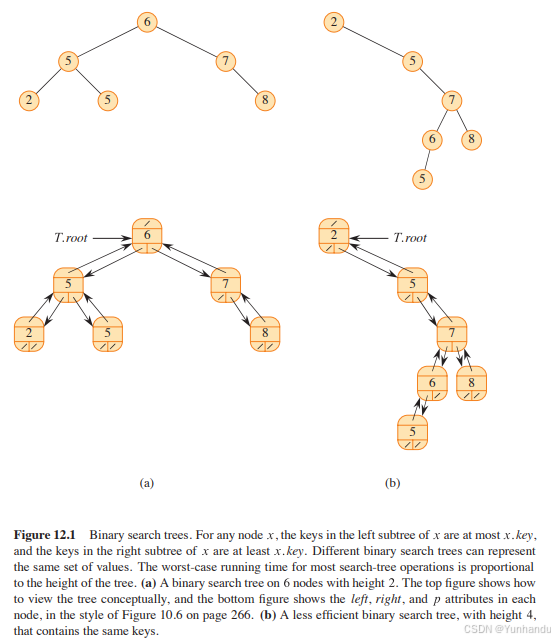
顾名思义，一棵BST是以一棵二叉树来组织的，如图12-1所示，这样一棵树可以使用一个链表数据结构来表示，其中每个节点就是一个对象。除了key_和卫星数据，每个节点有属性left child, right child和parent。（我在c++实现里参考了数据结构（c++语言版）额外加了一个属性，height），如果某child节点和parent节点不存在，则其相应的属性值为NIL。（c++实现中我直接用nullptr表示NIL）根节点是树中唯一父指针为NIL的节点。
在这里插入图片描述

BST的节点c++实现如下:

#define stature(node) ((node) ? (node)->height_ : -1)


template<typename T> struct TreeNode {
    T data_;
    TreeNode<T>* parent_;
    TreeNode<T>* lc_;
    TreeNode<T>* rc_;
    int height_;
    TreeNode() : parent_(nullptr), lc_(nullptr), rc_(nullptr), height_(0) {}
    TreeNode(T data, TreeNode<T>* parent = nullptr, TreeNode<T>* lc = nullptr,
             TreeNode<T>* rc = nullptr, int h = 0) : 
             data_(data), parent_(parent), lc_(lc), rc_(rc), height_(0) {}
    TreeNode<T>* insertAsLC(T const& lcVal);
    TreeNode<T>* insertAsRC(T const& lcVal);
    // Traversal Method
    template <typename VST> void travelLevel(VST& visit) { TravelLevel(this, visit); }
    template <typename VST> void travelPre(VST& visit) { TravelPreIterative(this, visit); }
    template <typename VST> void travelIn(VST& visit) { TravelInIterative(this, visit); }
    template <typename VST> void travelPost(VST& visit) { TravelPostRecursive(this, visit); }
};

在图12-1(a)中，树根的关键字为6，在其左子树中有关键字2,5和5，它们均不大于6；而在其右子树中有关键字7和8，它们均不小于6。这条性质对树中的每个节点都成立：在一棵BST中，任一节点r的左（右）子树中，所有的节点（若存在）的关键字均不大于(不小于)r的关键字。

该条性质允许我们通过简单的递归算法来按照关键字顺序访问BST中的节点，这种算法称为中序遍历, 这样命名的原因是访问的子树根节点的顺序在其左子树后，其右子树之前。我们可以看一下TravelInorderRecursive的c++实现:

/**
 * Traverses the given binary tree in in-order fashion using recursion.
 *
 * @tparam T The type of data stored in the tree nodes.
 * @tparam VST The type of the visitor object.
 * @param node The root node of the tree to be traversed.
 * @param visit The visitor object used to perform an operation on each visited node.
 */
template <typename T, typename VST>
void TravelInorderRecursive(TreeNode<T>* node, VST& visit) {
    if (!node) return;
    TravelPostRecursive(node->lc_, visit);
    visit(node); 
    TravelPostRecursive(node->rc_, visit);       
}

作为一个例子，对于图12-1中的2棵BST，中序遍历访问次序均为2， 5， 5，6，7，8。

额外提一嘴，我们要实现打印BST整体结构的话，也可以借助二叉树的中序遍历思想，详见12.2节的读操作。

TravelINorder的迭代版本，与先序遍历，后序遍历，层序遍历的实现请见附录中BST的整体实现代码。

遍历一棵有n个节点的BST要耗费 $\Theta(n)$ , 因为初次调用之后，对于树中的每个节点该遍历过程恰好自己要调用2次：1次是它的left child, 另一次是它的right child。下面的定理给出了执行一次中序遍历耗费线性时间的一个证明。

定理12.1 如果x是一棵有n个节点子树的根，那么调用TravelInorderRecursive需要 $\Theta(n)$ 时间。

证明： 当TravelInorderRecursive作用于一棵有n个节点子树的根时，用 $T (n)$ 表示需要的时间。由于TravelInorderRecursive要访问这棵子树的全部n个节点，所以有 $\Omega(n)$ 。下面要证明 $T (n) = O (n)$ 。

由于对于一棵空树，TravelInorderRecursive需要耗费一个小的常数时间c（c > 0, 因为要测试 node是否是NIL）, 有 $T (0) = c$ 。
对 $n > 0$ ，假设TravelInorderRecursive 作用在一个节点x上，x节点左子树有k个节点且其右子树有 n-k-1个节点，则执行TravelInorderRecursive的时间由 $T(n)\leq T(k) + T(n-k-1)+d$ ，其中常数 $d > c > 0$ , d为visit(x)的耗时。此式反应了执行TravelInorderRecursive的一个时间上界，其中不包括递归调用所花的时间。

使用替换法和数学归纳法，通过证明 $\leq (c+d)n + c$ ，可以证得 $T (n) = O (n)$ 。对于$ n = 0$ ，我们有 $(c + d) 0 + c = T (0)$ , $T(0)\leq c$ 成立，对于 $n = 1$ , 我们有 $2 c + d = T (1)$ , $T(1)\leq (c+d)*1 +c$ 成立。

假设 $\leq (c+d)*(j+1)$ 对于 $j = k$ 与 $j = n - k - 1$ 成立, 其中 $\geq 0$ ， $1\geq 0$ 。

我们有：
$\begin{aligned} T(n) &\leq T(k) + T(n-k-1)+d \\ & \leq ((c+d)k +c) +((c+d)(n-k-1) +c) + d \\ & = ((c+d)n -(c+d)+2c + d \\ & = ((c+d)n + c \\ \end{aligned}$
$\leq (c+d)*j + c$ 对于 $j = n$ 成立，定理得证。

对于12.2节的所涉及的所有读操作与12.3节的所有写操作，我们的BST的数据结构c++实现框架如下：

// author: Claude Du
template <typename T> class BST {
protected:
    int size_; TreeNode<T>* root_; // size_ means # of nodes
    virtual int UpdateHeight(TreeNode<T>* node);
    void UpdateHeightAbove(TreeNode<T>* node);
    void Display(TreeNode<T>* cur, int depth = 0);
    void Transplant(TreeNode<T>* toBeSubstituted, TreeNode<T>* vertex);
public:
    BST() : size_(0), root_(nullptr) {}    
    ~BST() { 
        if (size_ > 0) {
            std::cout << "Hi, my job is done. " << "\n";
            std::cout << Remove(root_);
        }
    }
    int size() const { return size_; }
    int height() const { return stature(root_); }
    bool empty() const { return root_ == nullptr; }
    TreeNode<T>* root() const { return root_; }
    // read operations:
    TreeNode<T>* TreeMinimum() const {
        if (root_ == nullptr) return root_; 
        return TreeMinimum(root_); 
    }

    TreeNode<T>* TreeMinimum(TreeNode<T>* cur) const;
    TreeNode<T>* TreeMaximum() const {
        if (root_ == nullptr) return root_; 
        return TreeMaximum(root_); 
    }
    TreeNode<T>* TreeMaximum(TreeNode<T>* cur) const;
    TreeNode<T>* TreeSuccessor(TreeNode<T>* cur) const;
    TreeNode<T>* TreePredecessor(TreeNode<T>* cur) const;
    // search
    TreeNode<T>*& TreeSearch(T const& keyVal);
    TreeNode<T>*& TreeSearchRecursive(TreeNode<T>*& cur, T const& keyVal);
    TreeNode<T>* TreeSearchIterative(TreeNode<T>* cur, T const& keyVal);
    // insertion
    TreeNode<T>* TreeInsert(T const& val);
    // deletion
    bool TreeDeletion(T const& val);
    void TreeDeletion(TreeNode<T>*& cur);
    void TreeDeletion2(TreeNode<T>* cur);
    int Remove(TreeNode<T>* x);
    // Traversal
    template <typename VST>
    void travLevel(VST& visit) { if (root_) root_->travLevel(visit); }
    template <typename VST>
    void travelPre(VST& visit) { if (root_) root_->travelPre(visit); }
    template <typename VST>
    void travelIn(VST& visit) { if (root_) root_->travelIn(visit); }
    template <typename VST>
    void travelPost(VST& visit) { if (root_) root_->travelPost(visit); }
    
    void Display();
};

12.2 查询BST（读操作）

BST支持这些查询操作：查找–TreeSearch，最大关键字元素–TreeMaximum，最小关键字元素–TreeMinimum，后继–TreeSuccessor 和前驱–TreePredecessor。本节会讨论这些操作与c++实现细节，并说明在任何高度为h的BST上，如何在 $O (h)$ 时间内执行完每个操作。

这些操作相对简单一些，原书讲解的很棒，我这里不会再重复叙述每个操作的具体细节。

查找–TreeSearch

我们使用TreeSearch过程来在一棵BST中查找一个有给定关键字的节点。输入一个指向某子树根节点的x和一个关键字k，TreeSearch返回一个指向关键字为k的节点的指针，否则返回NIL。

利用BST的关键性质，TreeSearch递归版c++实现如下：

template <typename T> TreeNode<T>*& BST<T>::TreeSearchRecursive(TreeNode<T>*& cur, T const& keyVal) {
    if (cur == nullptr || keyVal == cur->data_) return cur;
    if (keyVal < cur->data_)
        return TreeSearchRecursive(cur->lc_, keyVal);
    return TreeSearchRecursive(cur->rc_, keyVal);      
}

我们可以用while循环来展开递归，用一种迭代方式来重写这个这个过程，对于大多数计算机，迭代版效率更好，（减少了函数栈开销）TreeSearch迭代版c++实现如下：

template <typename T> TreeNode<T>* BST<T>::TreeSearchIterative(TreeNode<T>* cur, T const& keyVal) {
    while (cur != nullptr && keyVal != cur->data_) {
        if (keyVal < cur->data_) cur = cur->lc_;
        else cur = cur->rc_;
    }
    return cur;
}

无论是哪个版本，TreeSearch的时间复杂度为 $O (h)$ 。

最大关键字元素–TreeMaximum和最小关键字元素–TreeMinimum

这两个过程的c++实现如下：

template <typename T> TreeNode<T>* BST<T>::TreeMinimum(TreeNode<T>* cur) const {
    while (cur->lc_ != nullptr) {
        cur = cur->lc_;
    } 
    return cur;  
}
template <typename T> TreeNode<T>* BST<T>::TreeMaximum(TreeNode<T>* cur) const {
    while (cur->rc_ != nullptr) {
        cur = cur->rc_;
    } 
    return cur;  
}

TreeMinimum和TreeMaximum的时间复杂度为 $O (h)$ 。

后继–TreeSuccessor 和前驱–TreePredecessor

TreeSuccessor与TreePredecessor的c++实现如下：

template <typename T> TreeNode<T>* BST<T>::TreeSuccessor(TreeNode<T>* cur) const {
    if (cur->rc_ != nullptr) return TreeMinimum(cur->rc_);
    TreeNode<T>* y = cur->parent_;
    while (y != nullptr && cur == y.rc_) {
        cur = y;
        y = y->parent_;
    }
    return y;
}
template <typename T> TreeNode<T>* BST<T>::TreePredecessor(TreeNode<T>* cur) const {
    if (cur->lc_ != nullptr) return TreeMaximum(cur->lc_);
    TreeNode<T>* y = cur->parent_;
    while (y != nullptr && cur == y.lc_) {
        cur = y;
        y = y->parent_;
    }
    return y;
}

TreeSuccessor 和 TreePredecessor的时间复杂度为 $O (h)$ 。

还有一个额外的可以打印整个BST的读操作Display, 使用中序遍历的方式进行节点访问与打印节点值与节点对应的高度，其c++实现如下：

template <typename T>
void BST<T>::Display(TreeNode<T>* cur, int depth) {
    if (cur->lc_) Display(cur->lc_, depth + 1);

    for (int i=0; i < depth; i++)
        printf("     ");

    if (cur->parent_ != nullptr) {
        if ( cur == cur->parent_->lc_) {
            printf("L----");
        } else printf("R----");
    }
    std::cout << "[" << cur->data_ << "] - (" << cur->height_ << ")" << "\n";
    if (cur->rc_) Display(cur->rc_, depth + 1);    
}
template <typename T> void BST<T>::Display() {
    std::cout << "\n";
    if (root_ != nullptr) Display(root_);
    else std::cout << "Empty";
    std::cout << "\n";
}

打印效果如下：

          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (3)
               L----[9] - (0)
          L----[10] - (1)
               R----[11] - (0)
     R----[12] - (2)
          R----[13] - (1)
               R----[16] - (0)

12.3 插入和删除（写操作）

插入–TreeInsert

向一棵BST中插入一个关键字为val的新节点，其过程TreeInsert c++实现如下：

template <typename T> TreeNode<T>* BST<T>::TreeInsert(T const& val) {
    TreeNode<T>* targetPosiParent = nullptr;
    TreeNode<T>* curPosi = root_;
    while (curPosi != nullptr) {
        targetPosiParent = curPosi;
        if (val < curPosi->data_) curPosi = curPosi->lc_;
        else curPosi = curPosi->rc_;
    }
    TreeNode<T>* newNode = new TreeNode<T>(val, targetPosiParent);
    ++size_;
    // if tree is empty
    if (targetPosiParent == nullptr) {
        root_ = newNode;   
        return newNode;
    }
    if (val < targetPosiParent->data_) {
       targetPosiParent->lc_ = newNode; 
    } else targetPosiParent->rc_ = newNode;
    UpdateHeightAbove(newNode);
    return newNode;
}

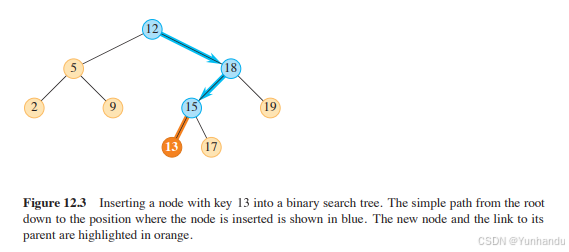
图12-3显示了TreeInsert是如何工作的。

在这里插入图片描述

TreeMaximum的时间复杂度为 $O (h)$ ，其中h为树的高度。

删除–TreeDeletion

从一颗BST中删除一个节点z（假设删除该节点前，BST一定储存了该节点）的整个策略可以分为如下三种基本情况：

基本情况1：如果z没有child, 那只用简单地将它删除–通过修改它的父节点，用nullptr作为孩子替换z。
基本情况2：如果z只有一个child，那么把该child提升到树中z的位置即可（相应算法实现稍后讲）。（中文第三版中相应的表述个人认为属于翻译错误）
基本情况3：如果z有2个child, 则先找到z的后继y(一定在z的右子树中并且没有左孩子)，让y占据树中z的位置。z原来右子树部分成为y的新右子树，并让z的左子树成为y的新左子树，此情形的相应算法实现有些棘手，因为还与y是否是z的right child相关。

删除节点z的程序TreeDeletion会取指向该BST和节点z的指针作为输入参数（在我的c++实现里，指向BST的指针就是BST类的this指针，所以不会显示表示该参数），之前划分的三种情形可以重组拆分成如下的更适用于我们算法实现的四种情形：

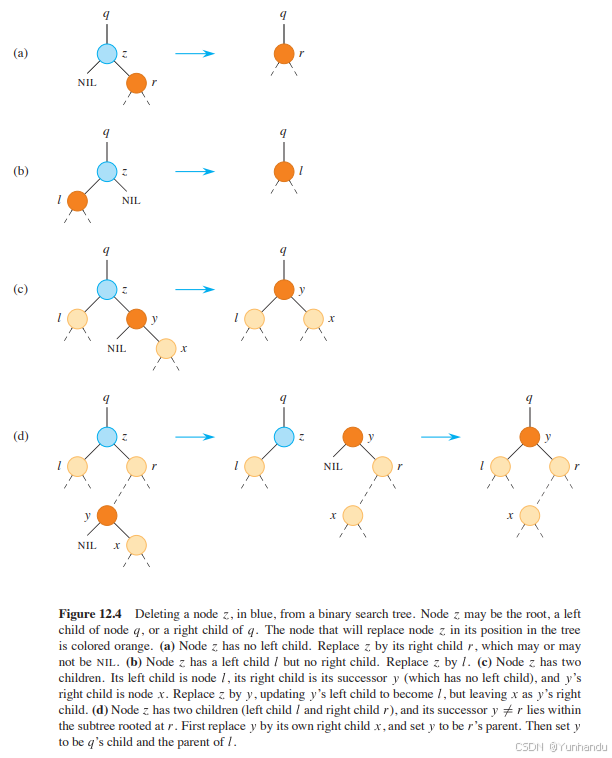
a. 节点z没有left child（如图12.4 a）, 那么用z的right child替换z, z可以是nullptr(对应基本情况1)，也可以不是nullptr。(对应基本情况2中z只有right child )
b. 节点z没有right child（如图12.4 b）, 那么用z的left child替换z（对应基本情况2中z只有left child）
否则，z一定有2个child，则先找到z的后继y。(一定在z的右子树中并且没有左孩子)：
c. 如果y是z的right child（如图12.4 c）, 那么用y替换z。（对应基本情况3中y是z的right child）
d. 否则，y不是z的right child（如图12.4 d)，在这种情况下，先用y的右孩子替换y，然后再用y替换z。（对应基本情况3中y不是z的right child）

图12.4如下：

在这里插入图片描述

为了在二叉树内移动子树，定义一个子过程Transplant, 它用一棵子树A(代码中vertex) 替换一棵子树B(代码中toBeSubstituted)并成为B(代码中toBeSubstituted)在其parent原来相应的child节点，其c++实现如下：

template <typename T> void BST<T>::Transplant(TreeNode<T>* toBeSubstituted, TreeNode<T>* vertex) {
    if (toBeSubstituted->parent_ == nullptr) root_ = vertex;
    else if (toBeSubstituted == toBeSubstituted->parent_->lc_) {
        toBeSubstituted->parent_->lc_ = vertex;
    } else toBeSubstituted->parent_->rc_ = vertex;
    if (vertex != nullptr) vertex->parent_ = toBeSubstituted->parent_;
}

利用现成的Transplant过程，下面是从二叉树T中删除节点的c++实现：

template <typename T> void BST<T>::TreeDeletion2(TreeNode<T>* z) {
    // node target is used to updateHeight, you may not put too much attention on it
    TreeNode<T>* target = z->parent_; // find the lowest node whose height may need to updated
    if (z->lc_ == nullptr) {
        Transplant(z, z->rc_); // case a: replace z by its right child
        
    } else if (z->rc_ == nullptr) {
        
        Transplant(z, z->lc_); // case b: replace z by its left child    
    } else {
        TreeNode<T>* y = TreeMinimum(z->rc_);
        if (y->parent_ != z) { // is y farther down the tree?
            // case d's first step: replace y by its right child 
            Transplant(y, y->rc_); 
            y->rc_ = z->rc_; // z's right child becomes
            y->rc_->parent_ = y; // y's right child
        }
        // case c's procedure is the same as case d's last step
        Transplant(z, y); // replace z by its successor y
        y->lc_ = z->lc_; // and give z's left child to y
        y->lc_->parent_ = y; // which had no left child
        target = (y->rc_ == nullptr) ? y : y-> rc_;     
    }
    UpdateHeightAbove(target);
    --size_;
}

c++实现中的target节点是用来维护删除过程中树中节点高度，非删除过程中的核心代码，可以不用给予过多关注。

TreeDeketion2的时间复杂度为 $O (h)$ ，其中h为树的高度。

13.4 附录

【1】二叉搜索树的整体c++代码实现如下：

BinarySearchTree.h

#ifndef BinarySearchTree_h
#define BinarySearchTree_h
// author: Claude Du
#include "TreeNode.h" 
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <cmath>
using std::vector;
using std::queue;
using std::stack;
template <typename T> class BST {
protected:
    int size_; TreeNode<T>* root_; // size_ means # of nodes
    virtual int UpdateHeight(TreeNode<T>* node);
    void UpdateHeightAbove(TreeNode<T>* node);
    void Display(TreeNode<T>* cur, int depth = 0);
    void Transplant(TreeNode<T>* toBeSubstituted, TreeNode<T>* vertex);
public:
    BST() : size_(0), root_(nullptr) {}    
    ~BST() { 
        if (size_ > 0) {
            std::cout << "Hi, my job is done. " << "\n";
            std::cout << Remove(root_);
        }
    }
    int size() const { return size_; }
    int height() const { return stature(root_); }
    bool empty() const { return root_ == nullptr; }
    TreeNode<T>* root() const { return root_; }
    TreeNode<T>* TreeMinimum() const {
        if (root_ == nullptr) return root_; 
        return TreeMinimum(root_); 
    }
    TreeNode<T>* TreeMinimum(TreeNode<T>* cur) const;
    TreeNode<T>* TreeMaximum() const {
        if (root_ == nullptr) return root_; 
        return TreeMaximum(root_); 
    }
    TreeNode<T>* TreeMaximum(TreeNode<T>* cur) const;
    TreeNode<T>* TreeSuccessor(TreeNode<T>* cur) const;
    TreeNode<T>* TreePredecessor(TreeNode<T>* cur) const;
    // search
    TreeNode<T>*& Search(T const& keyVal);
    TreeNode<T>*& SearchRecursive(TreeNode<T>*& cur, T const& keyVal);
    TreeNode<T>* SearchIterative(TreeNode<T>* cur, T const& keyVal);
    // insertion
    TreeNode<T>* TreeInsert(T const& val);
    // deletion
    bool TreeDeletion(T const& val);
    void TreeDeletion(TreeNode<T>*& cur);
    void TreeDeletion2(TreeNode<T>* cur);
    int Remove(TreeNode<T>* x);
    // Traversal
    template <typename VST>
    void travLevel(VST& visit) { if (root_) root_->travLevel(visit); }
    template <typename VST>
    void travelPre(VST& visit) { if (root_) root_->travelPre(visit); }
    template <typename VST>
    void travelIn(VST& visit) { if (root_) root_->travelIn(visit); }
    template <typename VST>
    void travelPost(VST& visit) { if (root_) root_->travelPost(visit); }
    void Display();
}; 

template <typename T> int BST<T>::UpdateHeight(TreeNode<T>* node) {
    node->height_ = 1 + std::max(stature(node->lc_), stature(node->rc_));
    return node->height_;
}
template <typename T> void BST<T>::UpdateHeightAbove(TreeNode<T>* node) {
    while (node) {
        UpdateHeight(node);
        node = node->parent_;
    }
}

template <typename T> TreeNode<T>* BST<T>::TreeMinimum(TreeNode<T>* cur) const {
    while (cur->lc_ != nullptr) {
        cur = cur->lc_;
    } 
    return cur;  
}
template <typename T> TreeNode<T>* BST<T>::TreeMaximum(TreeNode<T>* cur) const {
    while (cur->rc_ != nullptr) {
        cur = cur->rc_;
    } 
    return cur;  
}
template <typename T> TreeNode<T>* BST<T>::TreeSuccessor(TreeNode<T>* cur) const {
    if (cur->rc_ != nullptr) return TreeMinimum(cur->rc_);
    TreeNode<T>* y = cur->parent_;
    while (y != nullptr && cur == y.rc_) {
        cur = y;
        y = y->parent_;
    }
    return y;
}
template <typename T> TreeNode<T>* BST<T>::TreePredecessor(TreeNode<T>* cur) const {
    if (cur->lc_ != nullptr) return TreeMaximum(cur->lc_);
    TreeNode<T>* y = cur->parent_;
    while (y != nullptr && cur == y.lc_) {
        cur = y;
        y = y->parent_;
    }
    return y;
}
template <typename T> TreeNode<T>*& BST<T>::Search(T const& keyVal) {
    return SearchRecursive(root_, keyVal);    
}
template <typename T> TreeNode<T>*& BST<T>::SearchRecursive(TreeNode<T>*& cur, T const& keyVal) {
    if (cur == nullptr || keyVal == cur->data_) return cur;
    if (keyVal < cur->data_)
        return SearchRecursive(cur->lc_, keyVal);
    return SearchRecursive(cur->rc_, keyVal);      
}
template <typename T> TreeNode<T>* BST<T>::SearchIterative(TreeNode<T>* cur, T const& keyVal) {
    while (cur != nullptr && keyVal != cur->data_) {
        if (keyVal < cur->data_) cur = cur->lc_;
        else cur = cur->rc_;
    }
    return cur;
}

template <typename T> TreeNode<T>* BST<T>::TreeInsert(T const& val) {
    TreeNode<T>* targetPosiParent = nullptr;
    TreeNode<T>* curPosi = root_;
    while (curPosi != nullptr) {
        targetPosiParent = curPosi;
        if (val < curPosi->data_) curPosi = curPosi->lc_;
        else curPosi = curPosi->rc_;
    }
    TreeNode<T>* newNode = new TreeNode<T>(val, targetPosiParent);
    // if tree is empty
    ++size_;
    
    if (targetPosiParent == nullptr) {
        root_ = newNode;   
        return newNode;
    }
    if (val < targetPosiParent->data_) {
       targetPosiParent->lc_ = newNode; 
    } else targetPosiParent->rc_ = newNode;
    UpdateHeightAbove(newNode);
    return newNode;
}
template <typename T> bool BST<T>::TreeDeletion(T const& val) {
    TreeNode<T>*& cur = Search(val);
    if (cur == nullptr) return false;
    TreeDeletion2(cur); 
    return true;  
}
// Intro To Algo's Method
template <typename T> void BST<T>::Transplant(TreeNode<T>* toBeSubstituted, TreeNode<T>* vertex) {
    if (toBeSubstituted->parent_ == nullptr) root_ = vertex;
    else if (toBeSubstituted == toBeSubstituted->parent_->lc_) {
        toBeSubstituted->parent_->lc_ = vertex;
    } else toBeSubstituted->parent_->rc_ = vertex;
    if (vertex != nullptr) vertex->parent_ = toBeSubstituted->parent_;
}
template <typename T> void BST<T>::TreeDeletion2(TreeNode<T>* cur) {
    TreeNode<T>* target = cur->parent_; // find the lowest node whose height may need to updated
    if (cur->lc_ == nullptr) {
        Transplant(cur, cur->rc_); // replace cur by its right child
        
    } else if (cur->rc_ == nullptr) {
        Transplant(cur, cur->lc_); // replace cur by its left child    
    } else {
        TreeNode<T>* y = TreeMinimum(cur->rc_);
        if (y->parent_ != cur) { // is y farther down the tree?
            Transplant(y, y->rc_); // replace y by its right child
            y->rc_ = cur->rc_; // z's right child becomes
            y->rc_->parent_ = y; // y's right child
        }
        Transplant(cur, y); // replace cur by its successor y
        y->lc_ = cur->lc_; // and give z's left child to y
        y->lc_->parent_ = y; // which had no left child
        target = (y->rc_ == nullptr) ? y : y-> rc_;     
    }
    UpdateHeightAbove(target);
    --size_;
}
// 邓俊辉的取巧办法，我并不喜欢,有点取巧走后门的感觉
template <typename T> void BST<T>::TreeDeletion(TreeNode<T>*& cur) {
    TreeNode<T>* toBeDeleted = cur; // 
    TreeNode<T>* succ = nullptr;
    if (cur->lc_ == nullptr) {
        cur = cur->rc_;
        succ = cur;
    } else if (cur->rc_ == nullptr) {
        cur = cur->lc_;
        succ = cur;
    } else {
        toBeDeleted = TreeMinimum(toBeDeleted->rc_);
        std::swap(cur->data_, toBeDeleted->data_);
        TreeNode<T>* u = toBeDeleted->parent_;
        succ = toBeDeleted->rc_;
        if (u == cur) u->rc_ = succ;
        else u->rc_ = succ;
    }
    if (succ != nullptr) succ->parent_ = toBeDeleted->parent_;
    UpdateHeightAbove(toBeDeleted->parent_);
    --size_;
    delete toBeDeleted;
    toBeDeleted = nullptr;
    
}

template <typename T> int BST<T>::Remove(TreeNode<T>* x) {
    // cut the pointer from parent node
    TreeNode<T>* &pointerOfParent = (x->parent_ == nullptr) ? root_ : ((x == x->parent_->lc_) ? x->parent_->lc_ : x->parent_->rc_);
    pointerOfParent = nullptr;
    // Remove all the nodes of this subtree
    // use Preorder way to remove all the nodes.
    UpdateHeightAbove(x->parent_);
    int toBeDel = 0;
    auto del =[&toBeDel](TreeNode<T>* cur) {
        delete cur;
        cur = nullptr;
        ++toBeDel;
    };
    x->travelPre(del);
    size_ -= toBeDel;
    return toBeDel;
}
template <typename T> void BST<T>::Display() {
    std::cout << "\n";
    if (root_ != nullptr) Display(root_);
    else std::cout << "Empty";
    std::cout << "\n";
}
template <typename T>
void BST<T>::Display(TreeNode<T>* cur, int depth) {
    if (cur->lc_) Display(cur->lc_, depth + 1);

    for (int i=0; i < depth; i++)
        printf("     ");

    if (cur->parent_ != nullptr) {
        if ( cur == cur->parent_->lc_) {
            printf("┌───");
        } else printf("└───");
    }
    std::cout << "[" << cur->data_ << "] - (" << cur->height_ << ")" << "\n";
    if (cur->rc_) Display(cur->rc_, depth + 1);    
}

#endif /*BinarySearchTree_h*/

TreeNode.h

#ifndef TreeNode_h
#define TreeNode_h
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
using std::vector;
using std::queue;
using std::stack;
#define stature(node) ((node) ? (node)->height_ : -1)
template<typename T> struct TreeNode {
    T data_;
    TreeNode<T>* parent_;
    TreeNode<T>* lc_;
    TreeNode<T>* rc_;
    int height_;
    TreeNode() : parent_(nullptr), lc_(nullptr), rc_(nullptr), height_(0) {}
    TreeNode(T data, TreeNode<T>* parent = nullptr, TreeNode<T>* lc = nullptr,
             TreeNode<T>* rc = nullptr, int h = 0) : 
             data_(data), parent_(parent), lc_(lc), rc_(rc), height_(0) {}
    TreeNode<T>* insertAsLC(T const& lcVal);
    TreeNode<T>* insertAsRC(T const& lcVal);
    // Traversal Method
    template <typename VST> void travelLevel(VST& visit) { TravelLevel(this, visit); }
    template <typename VST> void travelPre(VST& visit) { TravelPreIterative(this, visit); }
    template <typename VST> void travelIn(VST& visit) { TravelInIterative(this, visit); }
    template <typename VST> void travelPost(VST& visit) { TravelPostRecursive(this, visit);}
};
// 1 level traversal
template <typename T, typename VST>  
void TravelLevel(TreeNode<T>* node, VST& visit) {
    queue<TreeNode<T>*> levelQue;
    
    levelQue.push(node);
    while (!levelQue.empty()) {
        TreeNode<T>* cur = levelQue.front();
        visit(cur);
        levelQue.pop();
        if (cur->lc_) {
            levelQue.push(cur->lc_);
        }
        if (cur->rc_) {
            levelQue.push(cur->rc_);
        }
    }
}
// 2.2 Iterative version of inorderTraversal
template <typename T, typename VST>
void TravelInIterative(TreeNode<T>* node, VST& visit) {
    stack<TreeNode<T>*> stk;
    TreeNode<T>* cur = node;
    while (cur || !stk.empty()) {
        if (cur) {
            stk.push(cur);
            cur = cur->lc_;
            continue;        
        }
        cur = stk.top();
        stk.pop();
        visit(cur);
        cur = cur->rc_;
    } 
}

// 3.2 Iterative version of Preorder traversal
template <typename T, typename VST>
void TravelPreIterative(TreeNode<T>* node, VST& visit) {
    stack<TreeNode<T>*> stk;
    TreeNode<T>* cur = node;
    stk.push(cur);
    while (!stk.empty()) {
        cur = stk.top();
        stk.pop();
        if (cur->rc_) stk.push(cur->rc_);
        if (cur->lc_) stk.push(cur->lc_);
        visit(cur);
    } 
}

// 4.1 recursive version of Postorder traversal
template <typename T, typename VST>
void TravelPostRecursive(TreeNode<T>* node, VST& visit) {
    if (!node) return;
    TravelPostRecursive(node->lc_, visit);
    TravelPostRecursive(node->rc_, visit);
    visit(node);    
}



#endif /*TreeNode_h*/

TreeNode.cpp

// author Yunhan Du
#include "TreeNode.h"
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
using std::vector;
using std::queue;
using std::stack;
template<typename T> TreeNode<T>* TreeNode<T>::insertAsLC(T const& lcVal) {
    lc_ = new TreeNode<T>(lcVal, this);
    return lc_;
}
template<typename T> TreeNode<T>* TreeNode<T>::insertAsRC(T const& rcVal) {
    rc_ = new TreeNode<T>(rcVal, this);
    return rc_;
}

template class TreeNode<int>;

main.cpp

// author: Claude Du
#include "TreeNode.h"
#include "BinarySearchTree.h"
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>

int main()
{
    // Test TreeNode
    TreeNode<int>* root = new TreeNode<int>(8);
    root->insertAsLC(5);
    root->insertAsRC(11);
    root->lc_->insertAsLC(3);
    root->lc_->insertAsRC(7);
    root->rc_->insertAsRC(12); 
    std::vector<int> record;
    auto visit = [&](TreeNode<int>* node) {
        record.emplace_back(node->data_);
        std::cout << node->data_ << " ";
    };
    root->travelLevel(visit);
    std::cout << "\n";
    record.clear();
    // Test BST
    BST<int> bst;
    bst.TreeInsert(8);
    bst.TreeInsert(12);
    bst.TreeInsert(5);
    bst.TreeInsert(3);
    bst.TreeInsert(7);
    bst.TreeInsert(13);
    bst.TreeInsert(10);
    bst.TreeInsert(11);
    bst.TreeInsert(9);
    bst.TreeInsert(16);
    bst.travelIn(visit);
    std::cout << "\n";
    std::cout << bst.size() << "\n";
    record.clear();
    bst.Display();
    bst.TreeDeletion(10);
    std::cout << bst.size() << "\n";
    bst.Display();
    bst.TreeDeletion(9);
    std::cout << bst.size() << "\n";
    bst.Display();
    bst.TreeDeletion(16);
    std::cout << bst.size() << "\n";
    bst.Display();
    std::cout << "TreeMaximum: " << bst.TreeMaximum()->data_ << "\n";
}

在terminal中执行：

g++ hello.cpp TreeNode.cpp -g

执行结果如下：

8 5 11 3 7 12 
3 5 7 8 9 10 11 12 13 16
10
The root is 8
THe found node is 7

          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (3)
               L----[9] - (0)
          L----[10] - (1)
               R----[11] - (0)
     R----[12] - (2)
          R----[13] - (1)
               R----[16] - (0)


               L----[3] - (0)
          L----[5] - (1)
               R----[7] - (0)
     L----[8] - (3)
               L----[9] - (0)
          R----[10] - (1)
               R----[11] - (0)
[12] - (2)
     R----[13] - (1)
          R----[16] - (0)


          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (3)
               L----[9] - (0)
          L----[10] - (1)
               R----[11] - (0)
     R----[12] - (2)
          R----[13] - (1)
               R----[16] - (0)

9

          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (3)
               L----[9] - (0)
          L----[11] - (1)
     R----[12] - (2)
          R----[13] - (1)
               R----[16] - (0)

8

          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (3)
          L----[11] - (0)
     R----[12] - (2)
          R----[13] - (1)
               R----[16] - (0)

7

          L----[3] - (0)
     L----[5] - (1)
          R----[7] - (0)
[8] - (2)
          L----[11] - (0)
     R----[12] - (1)
          R----[13] - (0)

TreeMaximum: 13
Hi, my job is done.
7