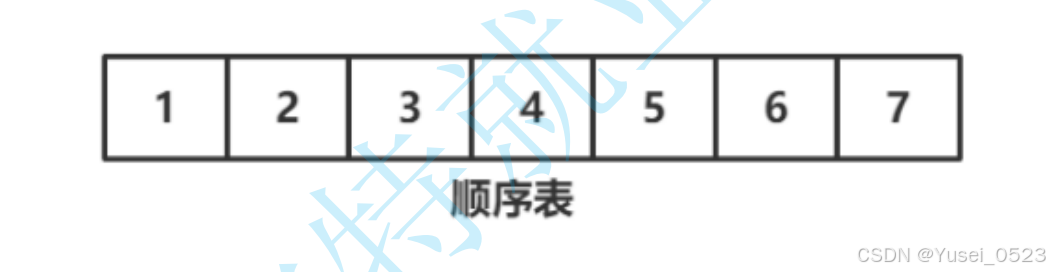
初阶数据结构2 顺序表和链表

顺序表

1. 线性表
2. 顺序表
- 2.1 概念与结构
2.2分类
2.3动态顺表表的实现
- 2.4 顺序表问题与思考
3.单链表
4. 双向链表
4.1 概念与结构
4.2双向链表的实现

1. 线性表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。线性表是⼀种在实际中⼴泛使⽤的数据结构，常⻅的线性表：顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构，也就说是连续的⼀条直线。但是在物理结构上并不⼀定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储
相同特性：逻辑结构和物理结构相同

逻辑结构:人为想象出来的数组的组织结构
物理结构:数组在内存的存储形式

2. 顺序表

2.1 概念与结构

概念：顺序表是⽤⼀段物理地址连续的存储单元依次存储数据元素的线性结构，⼀般情况下采⽤数组存储。
在这里插入图片描述

顺序表和数组的区别？
顺序表的底层结构是数组，对数组的封装，实现了常⽤的增删改查等接⼝。

2.2分类

静态顺序表：数组是定长的（往往不使用）

typedef int SLDatatype;//当想要更改数组元素类型时可以直接更改
//静态顺序表
typedef struct SeqList {
	SLDatatype array [N];
	int size;
};

动态顺序表:数组是根据需求重新开辟的

typedef int SLDatatype;
typedef struct SeqList {
	SLDatatype *arr;
	int capacity;//容量
	int size;//有效数据个数
}SL;

对数组封装我们还提供了两个属性容量和有效数据个数，当数组没有初始化时都是一些垃圾值，我们通过size可以标识数组中有效的数据个数，而容量对静态顺表表中就是定长数组的大小，对动态顺序表中则需要额外开辟。

2.3动态顺表表的实现

初始化 void SLInitialize(SL*s);

销毁 void SLDestroy(SL*s );

打印顺序表 void SLPrint(SL* ps);

插入数据检查容量 void SLCheckCapacity(SL* ps)；尾插 void SLPushBack(SL*s,
SLDatatype x);

头插 void SLPushFront(SL*s, SLDatatype x);

尾删 void SLPopBack(SL* s);

头删 void SLPopFront(SL* s);

在指定位置插入数据 void SLInsert(SL* s, SLDatatype x, int pos);

在指定位置删除数据 void SLErase(SL* s,int pos);

查找数据 int SLFind(SL* s, SLDatatype x);

编写代码

void SLInitialize(SL* ps)
{
	ps->arr = NULL;
	ps->capacity = ps->size = 0;
}

形参应为传址否则我们只是对实参进行了拷贝并没有真实修改实参

void SLDestroy(SL* ps)
{
	if (ps->arr)
	{
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->capacity = ps->size = 0;
}

一定要注意销毁顺序表时ps不能为空指针因为我们不能对空指针进行解引用（->）操作或者简便来写assert(ps)下同

void SLCheckCapacity(SL* ps)
{
	//判断空间是否充足
	if (ps->size == ps->capacity)
	{
		//增容//0*2 = 0
		//若capacity为0，给个默认值，否则×2倍
		int NewCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDatatype* tmp = (SLDatatype*)realloc(ps->arr, NewCapacity * sizeof(SLDatatype));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = NewCapacity;
	}
}

我们可能遇到capacity为0的情况此时我们可以用一个三目操作符对当capacity为0时提供一个默认值，我们扩容往往是进行二倍的扩容（这会造成空间的浪费，但是对内存反复的进行realloc会导致性能的下降，我们取其轻，同时realloc可能会开辟失败，为了保证程序的鲁棒性我添加了if条件，当新开辟的空间不为空指针，我们再将原数组指向新开辟的空间）

void SLPrint(SL* ps)
{
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->arr[i]);
	}
	printf("\n");
}

void SLPushBack(SL*ps, SLDatatype x)
{
	assert(ps);
	SLCheckCapacity(ps);
	ps->arr[ps->size++] = x;
}

进行插入操作时一定要检查容量是否充足，插入新数据时size即为下标的位置，同时插入操作不要忘记对size++
时间复杂度为O（1）


void SLPushFront(SL* ps, SLDatatype x)
{
	assert(ps);
	SLCheckCapacity(ps);
	//数据整体后移
	for (int i = ps->size; i > 0; i--)
	{
		ps->arr[i] = ps->arr[i-1];
	}
	ps->arr[0] = x;

	ps->size++;
}

时间复杂度为O（N）


void SLPopBack(SL* ps)
{
	assert(ps && ps->size);
	ps->size--;
}

时间复杂度为O(1)

void SLPopFront(SL* ps)
{
	assert(ps && ps->size);
	for (int i = 0; i < ps->size-1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}

时间复杂度为O（N）


void SLInsert(SL* ps, SLDatatype x, int pos)
{
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	for (int i = ps->size; i >pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[ps->size] = x;
	ps->size++;

}


void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size&& ps->size);
	for (int i=pos; i < ps->size-1; i++)
	{
		ps->arr[i] = ps->arr[i+1];
	}
	ps->size--;
}

时间复杂度为O(N )(最坏情况下)


int SLFind(SL* ps, SLDatatype x)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->arr[i] == x)
			return i;
	}
	return -1;
}

2.4 顺序表问题与思考

• 中间/头部的插⼊删除，时间复杂度为O(N)
• 增容需要申请新空间，拷⻉数据，释放旧空间。会有不⼩的消耗。
• 增容⼀般是呈2倍的增⻓，势必会有⼀定的空间浪费。例如当前容量为100，满了以后增容到200，
我们再继续插⼊了5个数据，后⾯没有数据插⼊了，那么就浪费了95个数据空间。

3.单链表

3.1 概念与结构

概念：链表是⼀种物理存储结构上⾮连续、⾮顺序的存储结构，数据元素的逻辑顺序是通过链表中的
指针链接次序实现的（人为实现）。
在这里插入图片描述

3.3.1结点

与顺序表不同的是，链表⾥的每节"⻋厢"都是独⽴申请下来的空间，我们称之为“结点”
结点的组成主要有两个部分：当前结点要保存的数据和保存下⼀个结点的地址（指针变量）。
图中指针变量 plist保存的是第⼀个结点的地址，我们称plist此时“指向”第⼀个结点，如果我们希望
plist“指向”第⼆个结点时，只需要修改plist保存的内容为0x0012FFA0。
链表中每个结点都是独⽴申请的（即需要插⼊数据时才去申请⼀块结点的空间），我们需要通过指针
变量来保存下⼀个结点位置才能从当前结点找到下⼀个结点。

3.1.2 链表的性质

1、链式机构在逻辑上是连续的，在物理结构上不⼀定连续
2、结点⼀般是从堆上申请的
3、从堆上申请来的空间，是按照⼀定策略分配出来的，每次申请的空间可能连续，可能不连续

3.2 实现单链表

typedef int SLTDataType;

定义结点结构;
typedef struct SListNode {
SLTDataType data;
struct SListNode* next;}SLTNode;

链表的打印
void SLTPrint(SLTNode*);
申请新结点 SLTNode* SLTBuyNode(SLTDataType);
插入数据
尾插
void SLTPushBack(SLTNode**, SLTDataType);
头插
voidSLTPushFront(SLTNode** , SLTDataType );

删除
尾删
void SLTPopBack(SLTNode**);
头删
void SLTPopFront(SLTNode**);

查找
SLTNode* SLTFind(SLTNode*, SLTDataType);

在指定位置之前插入数据
void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);

在指定位置之后插入数据
void SLTInsertAfter(SLTNode* pos, SLTDataType x);

删除pos结点
void SLTErase(SLTNode** pphead, SLTNode* pos);

删除pos之后的结点
void SLTEraseAfter(SLTNode* pos);

销毁链表
void SListDestroy(SLTNode** pphead);

编写代码

注意我这里用的都是二级指针，因为你想改变实参就一定要传地址，实参是一个一级指针要想改变它传参必须是传一个二级指针。同时插入等操作都应该先把新结点的指向确立

#define _CRT_SECURE_NO_WARNINGS 1
#include"SList.h"
void SLTPrint(SLTNode* phead)
{
	SLTNode* pcur = phead;
	while (pcur)
	{
		printf("%d->", pcur->data);
		pcur = pcur->next;
	}
	printf("NULL\n");
}

使用一个临时指针来改变进入循环而不是使用头指针（下同）

SLTNode* SLTBuyNode(SLTDataType x)
{
	SLTNode* node = (SLTNode*)malloc(sizeof(SLTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	node->data = x;
	node->next = NULL;

	return node;
}

void SLTPushBack(SLTNode**pphead, SLTDataType x)
{
	//申请新结点
	SLTNode*NewNode = SLTBuyNode(x);
	if (*pphead == NULL)
	{
		*pphead = NewNode;
	}
	//尾结点->新结点
	//找尾结点
	else
	{
		SLTNode* pcur = *pphead;
		while (pcur->next)
		{
			pcur = pcur->next;
		}
		pcur->next = NewNode;
	}
}

注意思考链表为空的情况，因为链表为空时找尾结点就对空指针解引用了

void SLTPushFront(SLTNode** pphead, SLTDataType x)
{
	assert(pphead);
	//申请新结点
	SLTNode* NewNode = SLTBuyNode(x);
	//进行头插
	NewNode->next = *pphead;
	*pphead = NewNode;
}

void SLTPopBack(SLTNode** pphead)
{
	//链表为空不可以删除
	assert(pphead && *pphead);
	//处理链表只有一个结点的情况
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	else
	{
		//找prev和ptail
		SLTNode* ptail = *pphead;
		SLTNode* prev = NULL;
		while (ptail->next)
		{
			prev = ptail;
			ptail = ptail->next;
		}
		prev->next = NULL;
		free(ptail);
		ptail = NULL;
	}
}

尾删要找尾结点和它的前驱结点，但是只有一个结点的情况下没有前驱结点

void SLTPopFront(SLTNode** pphead)
{
	//链表为空不可以删除
	assert(pphead && *pphead);
	SLTNode* next = (*pphead)->next;
	free(*pphead);
	*pphead = NULL;
	*pphead = next;
}

SLTNode* SLTFind(SLTNode* phead, SLTDataType x)
{
	SLTNode* pcur = phead;
	while (pcur)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		else
		{
			pcur = pcur->next;
		}
	}
	return NULL;
}

void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
	assert(pphead);
	assert(pos);
	if (*pphead == pos)
		SLTPushFront(pphead, x);
	else
	{
		SLTNode* prev = *pphead;
		SLTNode* NewNode = SLTBuyNode(x);
			while (prev->next != pos)
			{
				prev = prev->next;
			}
		prev->next = NewNode;
		NewNode->next = pos;
	}
}

插入指定结点影响的是前一个结点，但是头结点没有前一个结点因此我们要判断pos为头结点的情况

void SLTInsertAfter(SLTNode* pos, SLTDataType x)
{
	assert(pos);
	SLTNode* NewNode = SLTBuyNode(x);
	NewNode->next = pos->next;
	pos->next = NewNode;
}

void SLTErase(SLTNode** pphead, SLTNode* pos)
{
	assert(pphead&&*pphead);
	assert(pos);
	if (*pphead = pos)
		SLTPopBack(pphead);
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		prev->next = pos->next;
		free(pos);
		pos = NULL;
	}
}

删除当前结点影响的是它的前驱结点，但是头指针没有前驱结点所有要单独考虑

void SLTEraseAfter(SLTNode* pos)
{
	assert(pos && pos->next);
	SLTNode* del = pos->next;
	pos->next = pos->next->next;
	free(del);
	del = NULL;
}

void SListDestroy(SLTNode** pphead)
{
	SLTNode* pcur = *pphead;
	while (pcur)
	{
		SLTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}

4. 双向链表

4.1 概念与结构

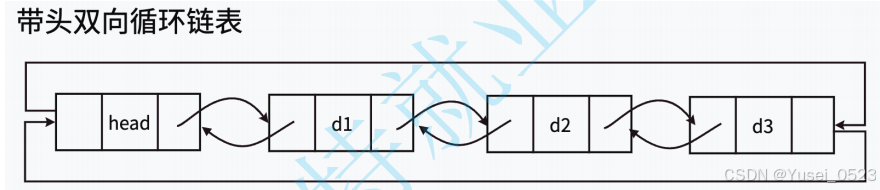
在这里插入图片描述

注意：这⾥的“带头”跟“头结点”是两个概念，带头链表⾥的头结点，实际为“哨兵位”，哨兵位结点不存储任何有效元素，只是站在这⾥“放哨"的

4.2双向链表的实现

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

定义双向链表节点的结构
typedef int LTDataType;
typedef struct ListNode
{
LTDataType data;
struct ListNode* next;
struct ListNode* prev;
}LTNode;

为了保持接口的一致性，优化接口都为一级指针
初始化
void LTInit(LTNode** pphead);
LTNode* LTInit();

销毁
void LTDesTroy(LTNode** pphead);
void LTDesTroy2(LTNode* phead);//传一级，需要手动将plist置为NULL

void LTPrint(LTNode* phead);

插入
void LTPushBack(LTNode* phead, LTDataType x);
void LTPushFront(LTNode* phead, LTDataType x);

删除
void LTPopBack(LTNode* phead);
void LTPopFront(LTNode* phead);

bool LTEmpty(LTNode* phead);

LTNode* LTFind(LTNode* phead, LTDataType x);
在pos位置之后插入节点
void LTInsert(LTNode* pos, LTDataType x);
删除指定位置节点
void LTErase(LTNode* pos);

编写代码

#define _CRT_SECURE_NO_WARNINGS 1
#include"list.h"
ListNode* BuyNode(LTDateType x)
{
	ListNode* NewNode = malloc(sizeof(ListNode));
	if (NewNode == NULL)
	{
		perror("Malloc Fail!");
		exit(1);
	}
	NewNode->data = x;
	NewNode->next = NewNode->prev = NewNode;
	return NewNode;
}

//void LTInitialise(ListNode** pphead)
//{
//	//创建一个头结点（哨兵卫）
//	*pphead = BuyNode(-1);
//}
ListNode* LTInitialise(ListNode*phead)
{
  phead=BuyNode(-1)
  return BuyNode(-1);
}

void LTDestroy(ListNode** pphead)
{
	assert(*pphead && pphead);
	ListNode*pcur = (*pphead)->next;
	while (pcur!=*pphead)
	{
		ListNode* Next = pcur->next;
		free(pcur);
		pcur = Next;
	}
	free(*pphead);
	*pphead = NULL;
	pcur = NULL;
}
//void LTDestroy(ListNode* phead)
//{
//	assert(phead);
//	ListNode* pcur = phead->next;
//	while (pcur != phead)
//	{
//		ListNode* Next = pcur->next;
//		free(pcur);
//		pcur = Next;
//	}
//	free(phead);
//	phead = NULL;
//	pcur = NULL;//实参手动置为空或者重新封装一个函数
//}

void LTPushBack(ListNode* phead, LTDateType x)
{
	assert(phead);
	ListNode* NewNode = BuyNode(x);
	NewNode->next = phead;
	NewNode->prev = phead->prev;
	phead->prev->next = NewNode;
	phead->prev = NewNode;
}

void LTPushFront(ListNode* phead, LTDateType x)
{
	assert(phead);
	ListNode* NewNode = BuyNode(x);
	NewNode->prev = phead;
	NewNode->next = phead->next;
	phead->next->prev = NewNode;
	phead->next = NewNode;
}

//打印双向链表
void LTPrint(ListNode* phead)
{
	ListNode* pcur = phead->next;
	while (pcur != phead)
	{
		printf("%d->", pcur->data);
		pcur = pcur->next;
	}
	printf("\n");
}

bool LTEmpty(ListNode* phead)
{
	if (phead->next == phead)
		return false;
	else
		return true;
}

void LTPopBack(ListNode* phead)
{
	assert(phead);
	assert(LTEmpty(phead));
	ListNode* del = phead->prev;
	ListNode* prev = del->prev;
	prev->next = phead;
	phead->prev = prev;
	free(del);
	del = NULL;
}

void LTPopFront(ListNode* phead)
{
	assert(phead);
	assert(LTEmpty(phead));
	ListNode* del = phead->next;
	ListNode* Next = del->next;
	Next->prev = phead;
	phead->next = Next;
	free(del);
	del = NULL;
}

ListNode* LTFind(ListNode* phead, LTDateType x)
{
	ListNode* pcur = phead->next;
	while (pcur != phead)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	return NULL;
}

void LTInsert(ListNode* pos,LTDateType x)
{
	assert(pos);
	ListNode* NewNode = BuyNode(x);
	NewNode->next = pos->next;
	NewNode->prev = pos;
	pos->next->prev = NewNode;
	pos->next = NewNode;
}

void LTErase(ListNode* pos)
{
	assert(pos);
	pos->prev->next = pos->next;
	pos->next->prev = pos->prev;

	free(pos);
	pos = NULL;
}

因为只有初始化结点和销毁结点我们需要对原来的实参进行修改，所以只有它传参是二级指针，而其他都是一级指针但是为了保持接口的一致性，优化接口都为一级指针。

尽管双向链表看起来比单向链表难，但实现起来却很简单，因为双向链表绝对有前驱结点和下一个结点，不会出现单链表时任意位置插入删除要判断是不是头结点啊（在单向链表中头结点没有前驱结点）的情况，也不用对链表为空单独考虑，因为当链表为空时它仍然有一个哨兵位