一、摘要

嗨喽呀大家，leetcode每日一题又和大家见面啦，今天要讲的是104.二叉树的最大深度，思路互相学习，有什么不足的地方欢迎指正！好啦让我们开始吧！！！

二、题目简介

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

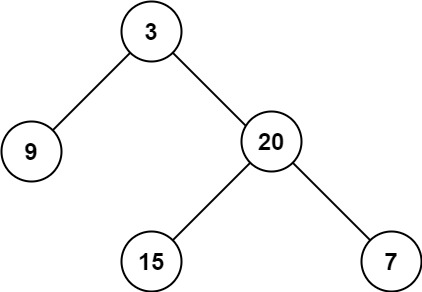
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

三、思路详解

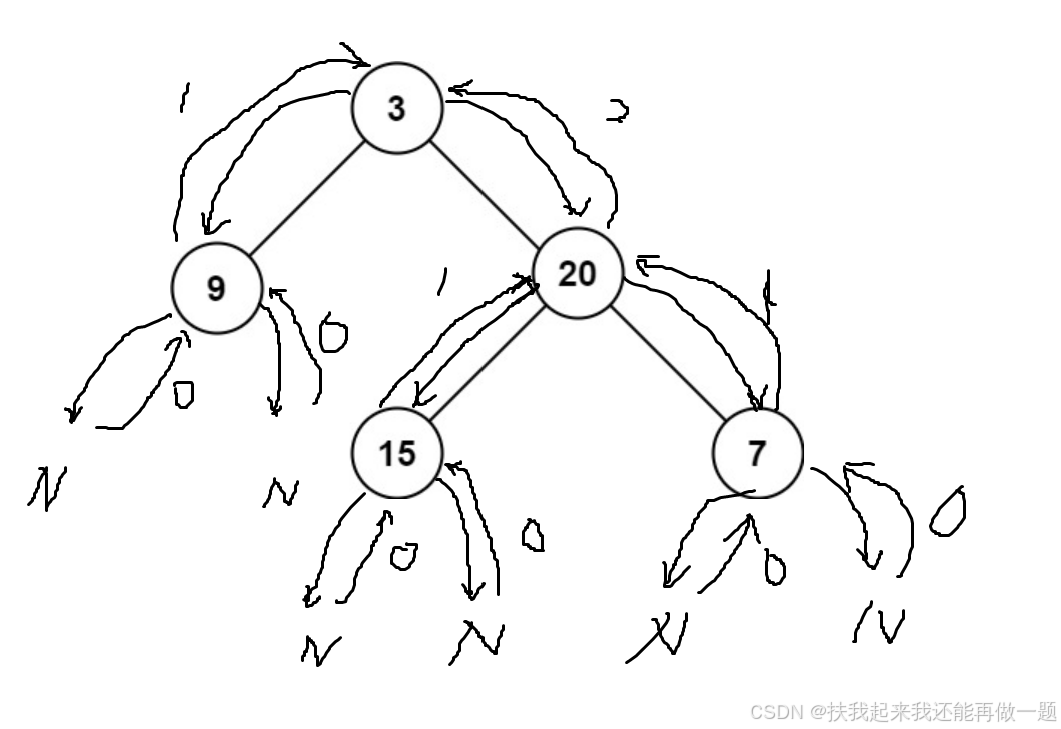
针对这道题我先补充一个递归的图像，能够帮我更好理解它递归的过程。图画由于是手画有点潦草

1. 递归法（深度优先搜索）

递归法是求解二叉树问题的常用方法。我们可以使用深度优先搜索（DFS）来遍历二叉树，找到从根节点到最远叶子节点的最长路径。

思路：

• 如果当前节点为空，返回深度 0。

• 递归计算左子树和右子树的最大深度。

• 当前节点的最大深度等于左子树和右子树的最大深度中的较大值加 1。

代码实现：

int maxDepth(struct TreeNode* root) {
    if (root == NULL) return 0;  // 空节点的深度为0

    // 递归计算左子树和右子树的最大深度
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    // 当前节点的最大深度为左右子树最大深度的较大值加1
    return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}

2. 迭代法（广度优先搜索）

迭代法使用队列来实现广度优先搜索（BFS），可以避免递归的深度限制问题。

思路：

• 使用一个队列来存储待访问的节点，每个节点附带其深度信息。

• 从根节点开始，将其深度设为 1。

• 遍历队列中的每个节点，更新最大深度。

• 将左右子节点（如果存在）加入队列，深度加 1。

代码实现：

int maxDepth(struct TreeNode* root) {
    if (root == NULL) return 0;  // 空树的最大深度为0

    struct TreeNode* queue[10000];  // 队列，假设最多10000个节点
    int depth[10000];  // 每个节点的深度
    int front = 0, rear = 0;
    int maxDepth = 0;

    queue[rear] = root;
    depth[rear] = 1;
    rear++;

    while (front < rear) {
        struct TreeNode* node = queue[front];
        int currentDepth = depth[front];
        front++;

        maxDepth = (currentDepth > maxDepth) ? currentDepth : maxDepth;

        if (node->left) {
            queue[rear] = node->left;
            depth[rear] = currentDepth + 1;
            rear++;
        }
        if (node->right) {
            queue[rear] = node->right;
            depth[rear] = currentDepth + 1;
            rear++;
        }
    }

    return maxDepth;
}

3. 前，中，后序遍历

思路：

• 后序遍历：先计算左子树和右子树的最大深度，再处理当前节点。

• 前序遍历：先处理当前节点，再计算左子树和右子树的最大深度。

• 中序遍历：先计算左子树的最大深度，处理当前节点，再计算右子树的最大深度。

• 在计算最大深度时，这些遍历顺序并没有实际影响，因为左右子树的最大深度是独立计算的，最终结果只取决于左右子树的最大深度。

• 二叉树的最大深度是从根节点到最远叶子节点的最长路径上的节点数。

• 无论采用哪种遍历顺序（前序、中序、后序），最终都需要计算左子树和右子树的最大深度，并取较大值加 1。

代码实现：

int maxDepth(struct TreeNode* root) {
    if (root == NULL) return 0;  // 空节点的深度为0

    // 递归计算左子树和右子树的最大深度
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);

    // 当前节点的最大深度为左右子树最大深度的较大值加1
    return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}

好啦，其实这类型的题目大致思路都是一样的，看完这些思路之后可以针对性的多做几道练习，今天的讲解就到这里啦。我们明天见！