背景知识:
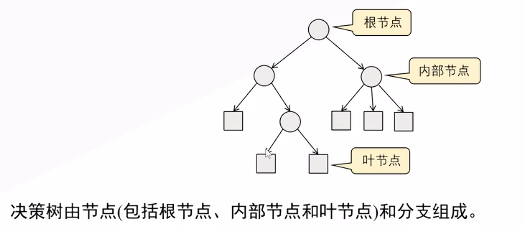
决策树是一种类似于流程图的树结构模型,它通过对数据特征的一系列测试和划分来进行决策或预测。
信息熵
信息熵体现了数据集中的不确定性程度。
●当信息熵较高时,表明数据中的不确定性大,预测难度增加
●信息熵较低则意味着不确定性小,数据更易于预测。
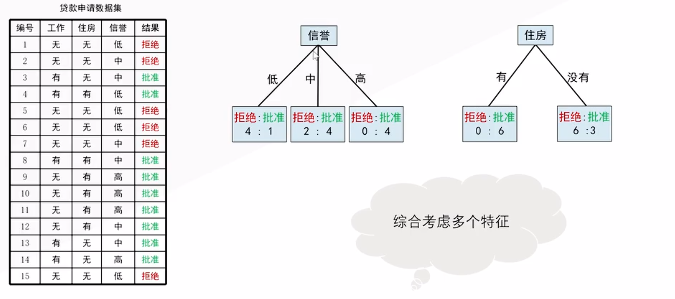
示例:考虑贷款申请数据集,只有批准和拒绝两个类,其中9个批准,6个拒绝。
条件熵:
条件熵表示在某属性A 的取值已知的情况下,数据集的不确定性:
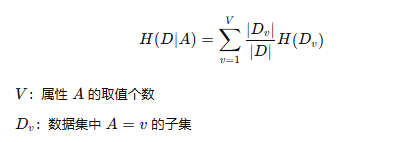
信息增益量
信息增益量化了选择某个特征进行划分后数据集纯度的提升,信息增益越大,该特征越适合作为决策树的分割条件。
【衡量某一属性对数据集分类的效果,表示使用该属性后数据集不确定性的减少量】
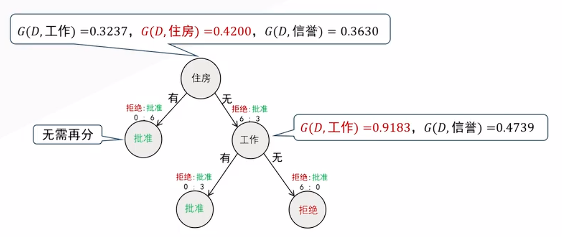
Gain(D,A) 越大,属性 A 对分类的贡献越大。
分类后,批准和拒绝两种情况的概率
前面是3个部分的加权平均
ID3算法
ID3算法是一种基于信息增益来选定决策树节点特征的算法。
通过不断选择信息增益最大的属性,将数据集划分为多个子集,最终构建决策树。
为了计算方便,写的时候可以分开写
计算数据集熵 H(D):
计算特征“Outlook”的信息增益:
计算每个子集 Dv的熵 H(Dv)。
Outlook分位sunny,rainy,overcast三点
计算每个子集的加权熵,并求出总熵
计算信息增益:用数据集熵减去总熵。
就这样计算每个特征,比较各特征的信息增益,选择信息增益最高的特征作为当前节点的划分依据。
ID3算法 是一种基于信息增益的决策树生成算法。以下总结其解决计算题的思路,并通过一个示例详细展示其计算过程。
ID3算法计算思路
-
根据给定的样本数据,构造决策树,找到使信息增益最大的划分属性。
-
步骤概述:
- 计算数据集的信息熵(Entropy)。
- 对每个属性,计算基于该属性划分的数据的条件熵(Conditional Entropy)。
- 计算信息增益: 信息增益=数据集熵−条件熵信息增益 = 数据集熵 - 条件熵信息增益=数据集熵−条件熵
- 选择信息增益最大的属性作为当前节点的划分属性。
- 递归进行划分,直至满足停止条件(如所有样本属于同一类,或属性集为空)。