Bootstrap

手撕七大排序(四)

快排的非递归实现

快排的递归我们上篇文章已将讲过了

可以参考手撕七大排序(三)-CSDN博客

这个时候就要用到我们的数据结构 栈了

我们首先先将我们需要排序的数组左右下标传递进去

之后我们开始进行一个循环操作

如果栈不为空 我们就执行这个循环

首先我们以这个数组的左边为例

通过第一趟排序 可以将整个数组分为三个部分

我们将中值设置为keyi

那么左边就是

begin~ keyi-1

右边就是

keyi+1~end

那么到这里我们的终止条件就很好判断了

begin<keyi1

keyi+1<end

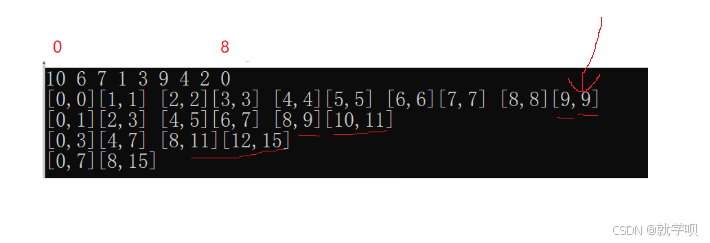
那么这里我们先将 0 ~ 9 出栈

之后将它分割的两边

6~9

0~4 依次进栈

如图

再之后我们将0~4进行出栈

判断有没有达到边界条件再进行压栈

整体代码表示如下

//快排非递归
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	//栈的方式 先进后出 后进先出
	//区间两两进 先进最初的区间
	STPush(&st, right);
	STPush(&st, left);

	while (!STEmpty(&st))
	{
		//先出左
		int begin = STTop(&st);
		STPop(&st);
		//再出右
		int end = STTop(&st);
		STPop(&st);
		//分割区间
		int keyi = PartSort3(a, begin, end);
		//[begin,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STPush(&st, keyi-1);
			STPush(&st, begin);
		}

	}

	STDestroy(&st);
}

归并排序递归写法

一. 基本概念

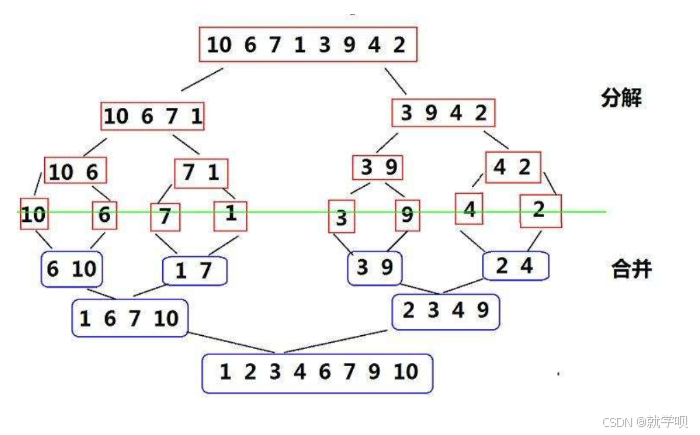
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

说了那么一大堆的话 其实中心思想就两个字 分治

二. 图解 

我们要将整个数组有序就是要将它的左右数组都变得有序

我们要想将左右数组都变得有序就是要将它左数组的左右数组和右数组的左右数组变得有序

依次套娃 到最后面呢

会变成一个个单个的元素 这个时候肯定是有序了嘛

 

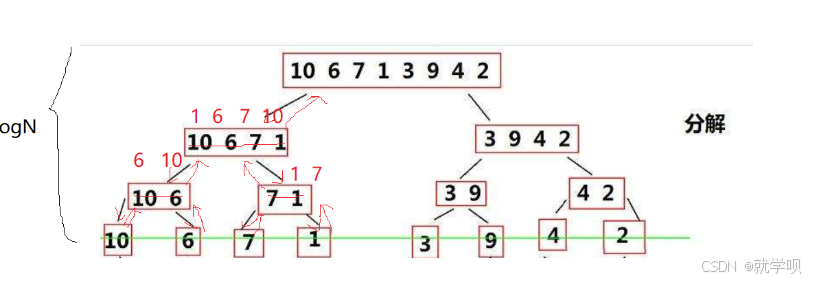
当它变成有序之后我们再一个一个的归并

我们来看代码

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("maoolc fail");
		return;
	}
	//最好用子函数 防止递归调用 重复开辟空间
	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
}

这里我们首先要创建一个临时的数组来归并存贮数据 不然的话再内部排序会打乱顺序

之后我们开始考虑递归的问题

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}
	//分割区间 
	int mid = (begin + end) / 2;
	//[begin,mid] [mid+1,end]
	//递归分区间
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

我们先来看这一段

这里开始递归如果没有达到边界条件的话 （只有一个元素）

就往左和右继续走

递完毕了之后我们开始归

这里注意看图

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}
	//分割区间 
	int mid = (begin + end) / 2;
	//[begin,mid] [mid+1,end]
	//递归分区间
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

	int begin1 = begin; int end1 = mid;
	int begin2 = mid + 1; int end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//一方遍历完 一方没遍历完
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	//将tmp拷贝到原数组
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

再之后我们将临时数组里面的值一一放到a里面就好啦

这里有一点要注意的是拷贝的位置

这里的a要+begin才可以

因为我们我们每次归的范围不同

归并排序的非递归写法

我们首先来看下递归的思路

这边是分解成单个的元素然后让它们进行归并

单个元素进行好之后归并之后就继续两个元素进行归并

两个元素进行好归并之后就继续四个元素进行归并

四个元素进行好归并之后就继续八个元素进行归并

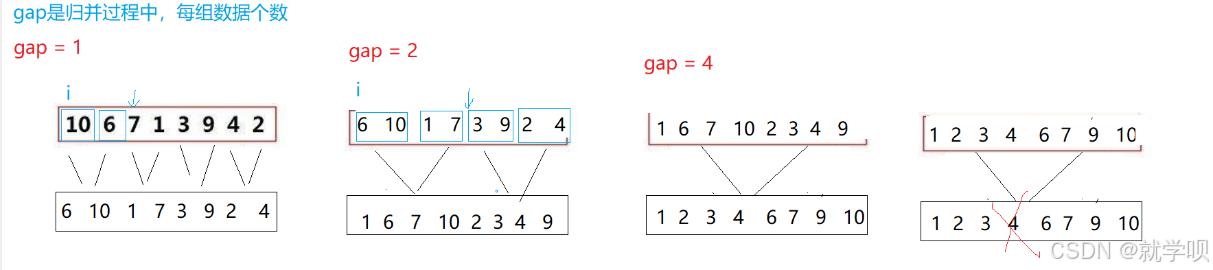
我们的非递归思路的主要思想就是用循环进行分割数组

如图

首先分割成八个

再之后分割成四个

再之后分割成两个

如果最后成为一个了之后

它就直接变成有序的了

我们这里的代码如下（其实就是照抄归那一段代码 修改了一小部分 ）

我们这里使用gap来进行分割

这是一个很巧妙的思路

当gap等于1的时候 数组就只有一个元素

当gap等于2的时候 数组就有两个元素

归并 非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//gap是归并过程中 每组个数
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2*gap)
		{
			//划分区间 [begin1,end1][begin2,end2]
			int begin1 = i; int end1 = i + gap - 1;
			int begin2 = i + gap; int end2 = i + 2 * gap - 1;
	
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			//一方遍历完 一方没遍历完
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}

		
		gap *= 2;
	}
	free(tmp);
}

当然最后我们需要将整个排序好的数组拷贝到原数组中

不然的话 的话其实就只是排序了最后一次 ！！

改bug

当然这里的代码肯定是不正确的

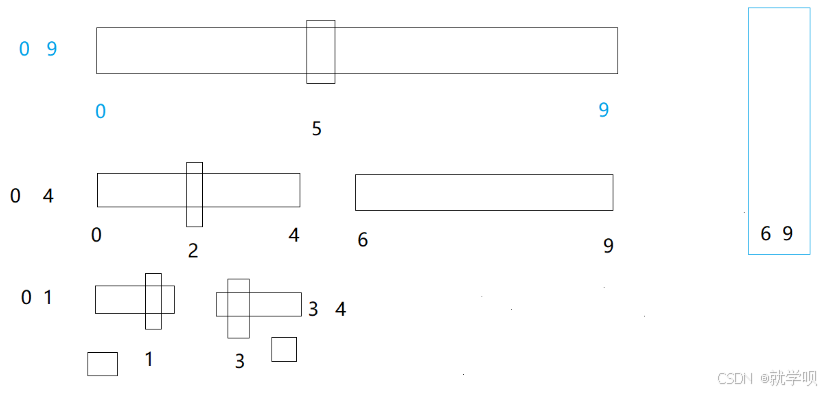
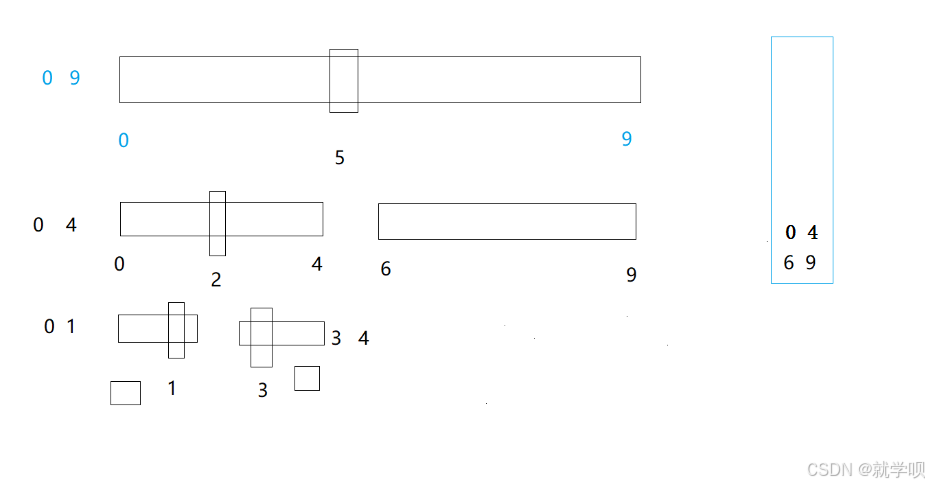
当我们的数组个数不是2的n次方的时候 这里的程序就会出现bug(越界问题)

如图

这里 是不是很明显的会造成一个数组越界的情况啊

我们仔细分析下

对于我们的三个边界

begin1肯定是不可能越界的

begin2 end1 end2都有可能越界

那这个时候怎么办呢？

我们就要根据这三种情况一一给出解决思路

当end1越界的时候我们是不是只要修正下边界就可以了

再将第二个数组置为不存在

当begin2越界的时候也是一个思路 置为不存在

当end2越界的时候呢 跟end1越界的思路一样 这里我们修正下边界就好

修正代码如下

//不为2的倍数会出现越界 
			//end1越界不归并 直接拷贝
			//begin2越界 和end1一样
			//end2越界 需要修正 归并
			if (end1 >= n)
			{
				end1 = n - 1;
				//让后面区间不存在
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n-1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

这种是间距为gap的多组数据归并完以后 一把拷贝(梭哈)的修正

完整代码如下

//归并 非递归
//一把拷贝(梭哈)
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//gap是归并过程中 每组个数
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2*gap)
		{
			//划分区间 [begin1,end1][begin2,end2]
			int begin1 = i; int end1 = i + gap - 1;
			int begin2 = i + gap; int end2 = i + 2 * gap - 1;
			//不为2的倍数会出现越界 
			//end1越界不归并 直接拷贝
			//begin2越界 和end1一样
			//end2越界 需要修正 归并
			if (end1 >= n)
			{
				end1 = n - 1;
				//让后面区间不存在
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n-1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			printf("[%d %d] [%d %d]", begin1, end1, begin2, end2);
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			//一方遍历完 一方没遍历完
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}

		printf("\n");
		//间距为gap的多组数据归并完以后 一把拷贝(梭哈)
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2;
	}
	free(tmp);
}

还有一种是归并一部分 拷贝一部分 （推荐这种写法）

修正如下

//不为2的倍数会出现越界 
			//end1越界不归并 直接拷贝
			//begin2越界 和end1一样
			//end2越界 需要修正 归并
			//不归并不需要拷贝 所以只修正end2越界
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

完整代码如下

//归并一部分 拷贝一部分
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//gap是归并过程中 每组个数
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//划分区间 [begin1,end1][begin2,end2]
			int begin1 = i; int end1 = i + gap - 1;
			int begin2 = i + gap; int end2 = i + 2 * gap - 1;
			//不为2的倍数会出现越界 
			//end1越界不归并 直接拷贝
			//begin2越界 和end1一样
			//end2越界 需要修正 归并
			//不归并不需要拷贝 所以只修正end2越界
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			printf("[%d %d] [%d %d]", begin1, end1, begin2, end2);
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			//一方遍历完 一方没遍历完
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			//归并一部分 拷贝一部分
			memcpy(a+i, tmp+i, sizeof(int) *(end2+1-i) );
		}

		printf("\n");
		gap *= 2;
	}
	free(tmp);
}

几个注意点

这里我们需要注意的点有三点

1. 注意排序完一次之后需要将临时数组里的内容拷贝回去
2. 注意begin1 begin2 end1 end2的边界 这个还是蛮难想的
3. 注意数组越界问题 对于三种可能越界情况要给予修正

以上便是本文所有内容，如有错误请各位大佬不吝赐教，感谢留言

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
海量元宇宙场景模板，视创云展解锁你的无限创意虚拟空间！
Ubuntu18.04离线安装驱动（离线！！！亲测）
机器学习分类光谱数据
毕业感悟
小米SU7交付10000台，大数据告诉你用户都在吐槽什么？
【elementUI系列二】el-image实现下载功能
图解CNN：通过100张图一步步理解CNN
基于SSM宠物信息交流平台JAVA|VUE|Springboot计算机毕业设计源代码+数据库+LW文档+开题报告+答辩稿+部署教+代码讲解
Kotlin入门学习(非常详细)，从零基础入门到精通，看完这一篇就够了
玩转python 时间戳转换
;