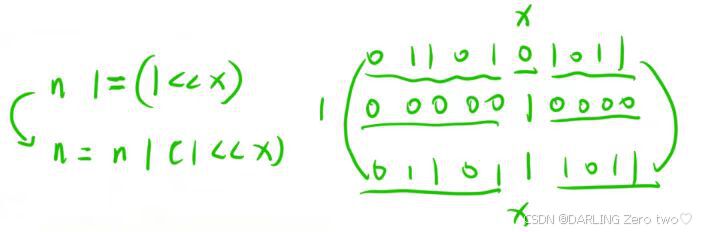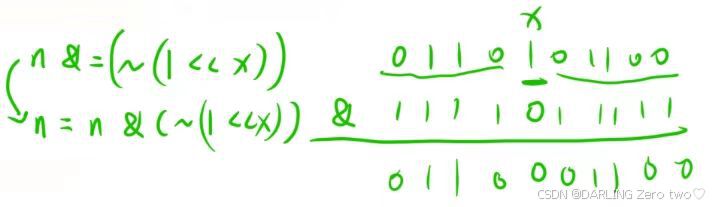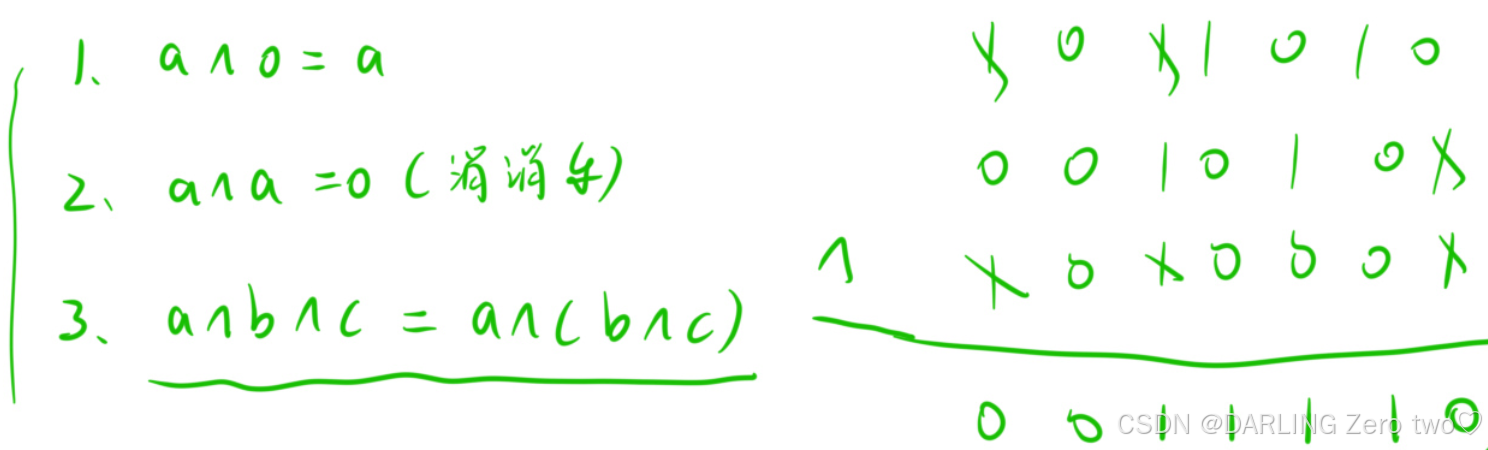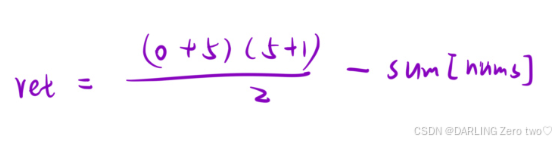文章目录
本篇是优选算法之位运算算法,这是一种直接对整数在内存中的二进制位进行操作的运算,它的运算效率高,在快速幂算法,汉明重量,找出数组中唯一出现一次的数字,不使用额外变量交换两个数
1.常见位运算总结
1.1 基础位运算符号
这六个位运算符是实现位运算算法的重要运算符,在C语言阶段有详细的介绍过
记法如图所示,强调一下什么是无进位相加?
异或运算的规则决定了它天然契合
无进位相加的概念
异或运算在比较两个二进制位时,0 ^ 0 = 0,0 ^ 1 = 1 ,1 ^ 0 = 1, 1 ^ 1 = 0
只是单纯对比两个数在每一位上的值,将不同的视为 1,相同的视为 0,不涉及向高位进位
1.2 给一个数 n,确定它的二进制表示中的第 x 位是 0 还是 1
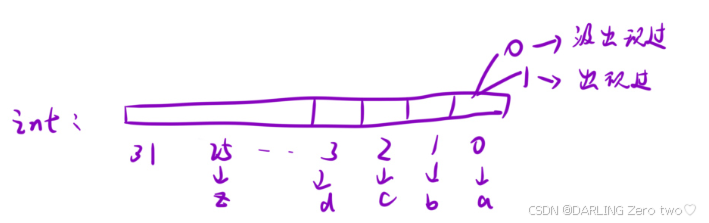
约定二进制位从右到左,为最低位到最高位,定义为从0到31,为的就是对应右移x位刚好对应第x位。所以将要比较的数 n 的第x位右移x位,与1按位与&,如果是0,第x位为0;如果是1,第x位是1
1.3 将一个数 n 的二进制表示的第 x 位修改成 1
要修改数n第x位为1就不能破坏原来的数,所以将1移动x位,与1按位或|,只修改了我们想要修改的那一位
1.4 将一个数 n 的二进制表示的第 x 位修改成 0
要修改数n第x位为0就不能破坏原来的数,所以将1移动x位,取反~为0,与1按位与&,只修改了我们想要修改的那一位
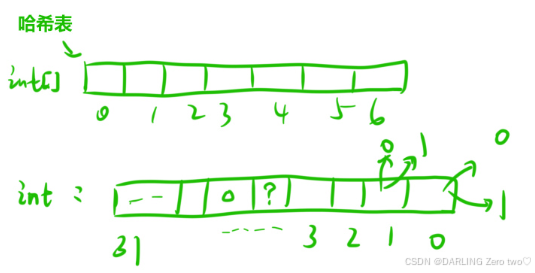
1.5 位图的思想
位图其实和哈希表相似,哈希表是额外开辟一个空间,计算数据出现频次,而位图则是把数据存在数据类型一个个字节里,这就省去了多开一个空间,然后利用上述的方法修改为1或0,统计数是否出现过
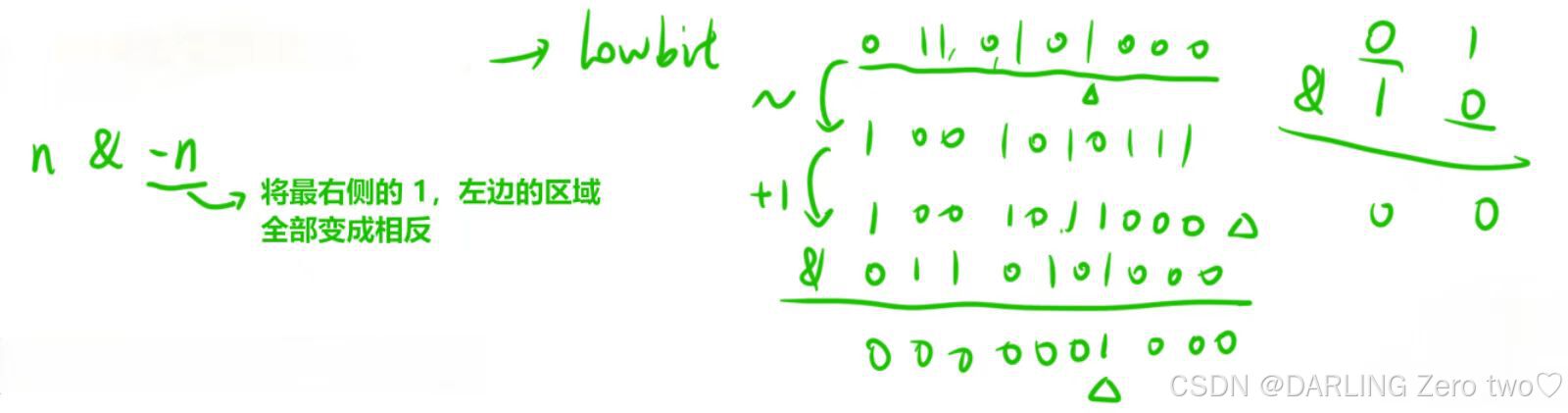
1.6 提取一个 n 二进制表示中最右侧的 1
将数n取反后+1得到相反数-n,然后两数按位与&得到最右侧的1。即最右侧的1及其右边都不变,左边的数都变成0
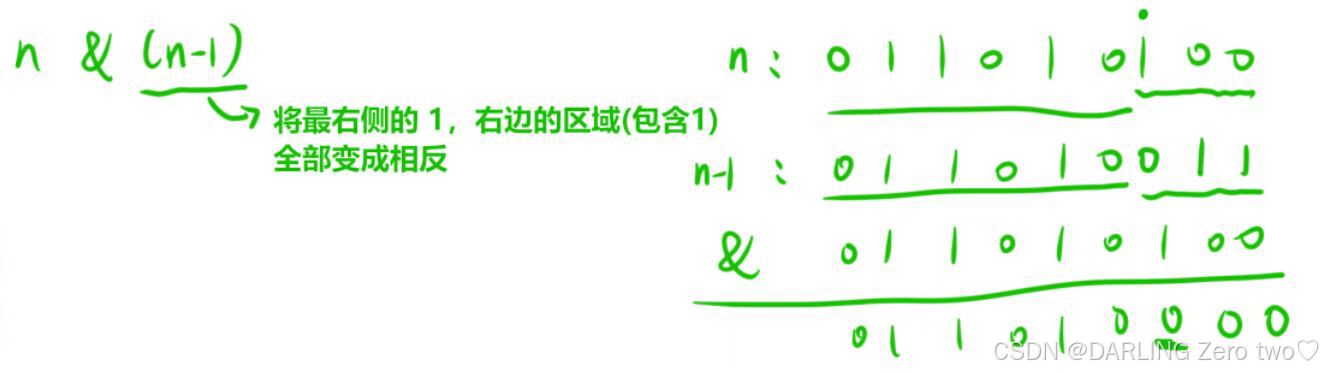
1.7 干掉一个数 n 二进制表示中最右侧的 1
将数n减1,然后两数按位与&干掉最右侧的1。即最右侧的1及其右边都变成0,左边的数都不变
1.8 位运算的优先级
通常优先级为:
~>&>^>|
但是记起来太麻烦了,干脆直接加括号更好
1.9 异或运算符 ^ 的运算律
这是异或运算符^常用的运算律,在题目中经常用
2.判定字符是否唯一
✏️题目描述:
✏️示例:
传送门:判定字符是否唯一
题解:
通常统计多数的字母出现次数一般想到的是哈希表,时间空间复杂度都为O(n),这就有人问了,有没有既简单又强势的方法能够解决?有的兄弟有的,这么强势的方法有九个,都是当前蓝桥杯T0.5的强势方法,因为本题只涉及26个小写英文字母,所以可以用减少开辟空间的位图
如上述介绍位图一样,用1和0表示字母是否出现过,如果为1,就返回false;如果是0,就添加1到指定位数上,遍历完字符串后返回true,
💻细节问题:
利用鸽巣原理,如果字符串长度大于26,那么必定有字母是重复的,所以大于26直接返回false
💻代码实现:
#include <iostream>
#include <string>
using namespace std;
class Solution
{
public:
bool isUnique(string astr)
{
if (astr.size() > 26)
{
return false;
}
int bitMap = 0;
for (auto ch : astr)
{
int i = ch - 'a';
if ((bitMap >> i) & 1 == 1)
{
return false;
}
bitMap |= 1 << i;
}
return true;
}
};
3.丢失的数字
✏️题目描述:
✏️示例:
传送门:丢失的数字
题解:
该题一共有四种方法解决
🚩哈希表
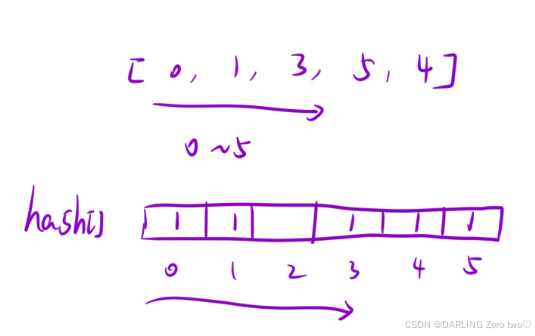
把0 ~ n中出现的所有数字都放进哈希表里,然后遍历一遍哈希表,如果某一格内对应的0,那么该数就是缺失的数字
🚩高斯求和
利用简单的求和公式求出0 ~ n所有数的和,然后减去缺失数字的数组,剩下的数就是题意所求
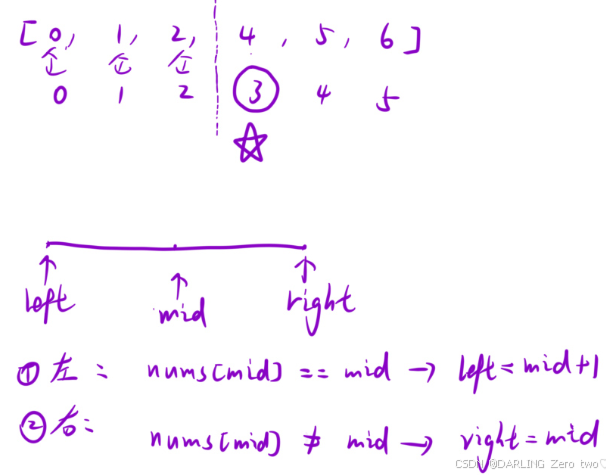
🚩二分查找
先对数组进行排序,在连续数组的前提下,缺失数字的位置开始下标与实际值不同,很明显二段性立马就出来了,如果在右区间,那么mid会有等于缺失值的实际位置索引,即right = mid;如果在左区间,mid及其前面的值都不可能是缺失值的实际位置索引,即left = mid + 1
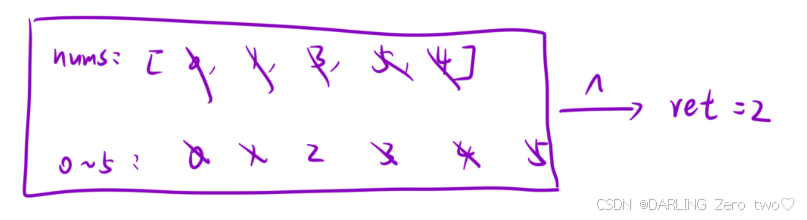
🚩位运算
根据异或运算^的运算律,相同的两个数异或会抵消成0,所以显而易见,把缺失数字的数组和完整的数组异或,剩下的就是缺失的数字
💻代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
int missingNumber(vector<int>& nums)
{
int ret = 0;
for (auto x : nums)
{
ret ^= x;
}
for (int i = 0; i <= nums.size(); ++i)
{
ret ^= i;
}
return ret;
}
};
4.两整数之和
✏️题目描述:
✏️示例:
传送门:两整数之和
题解:
很显然本题是一道为了笔试而出题的题,通常是不会要我们这样去计算的,如果是在笔试环节时,可以投机取巧,直接return a+b通过测试用例,一般面试官也不会去看你的代码
言归正传,该题主要使用异或运算+无进位相加解决
我们知道无进位相加就是只相加不进位,所以我们只要解决了进位问题,那么问题就迎刃而解了,那么进位也只会在两个位都为1的情况下才会进位,观察发现进位的操作就是按位与&,注意要进位的是下一位,所以要把按位与&完的结果右移一位。两个结果不断重复上述操作,直到进位为0,就是相加的最终结果
💻细节问题:
注意进位的数有可能因为
一直右移导致为-1,只要强转为无符号整数就行
💻代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
int getSum(int a, int b)
{
while (b != 0)
{
int x = a ^ b;
unsigned int carry = (unsigned int)(a & b) << 1;
a = x;
b = carry;
}
return a;
}
};
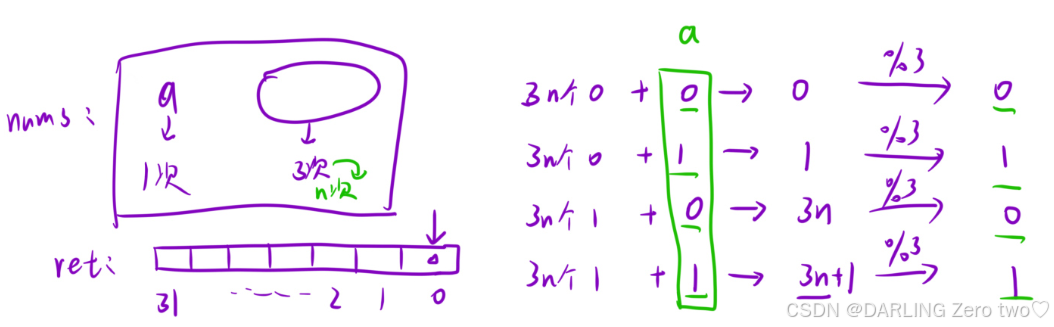
5.只出现一次的数字Ⅱ
✏️题目描述:
✏️示例:
传送门:只出现一次的数字Ⅱ
题解:
本题的解法是一种通用解法,以后遇到类似的题目思路是一样的,但是前提是要见过这种解法,这种思路十分的巧妙
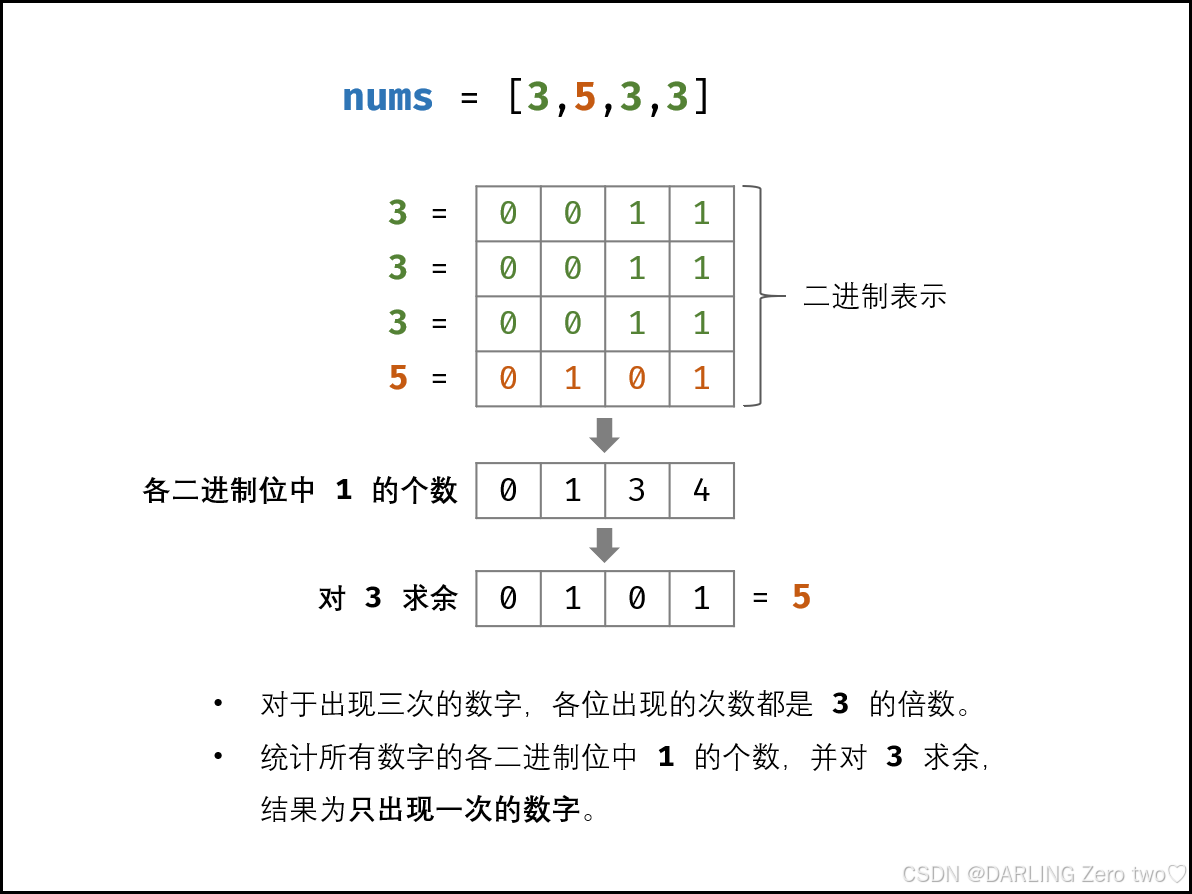
因为除去单独的数,每个数的一位必定出现三次,也就是三的倍数
所以每个数的指定位数之和必定为如图四种情况的一种,对加和总数求余数发现剩下的数就是那个单独的数的指定位数,很好,如此一来就发现了规律,如此循环往复,把每一位存入位图就能求出只出现一次的数
💻细节问题:
实际上本题还能改成
出现n次,只要把求余数时改成除n就行,其余的算法思路是一样的
💻代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
int ret = 0;
for (int i = 0; i < 32; ++i)
{
int sum = 0;
for (auto x : nums)
{
if (((x >> i) & 1) == 1)
{
sum++;
}
}
sum %= 3;
if (sum == 1)
{
ret |= 1 << i;
}
}
return ret;
}
};
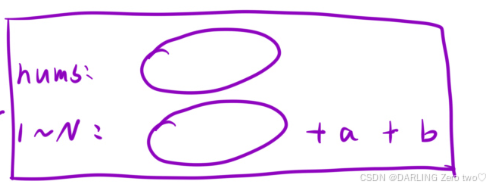
6.消失的两个数字
✏️题目描述:
✏️示例:
传送门:消失的两个数字
题解:
本题是丢失的数字的延伸扩展,难度可以说是上升不少,博主自己也想了好久才大彻大悟,但是掌握了这题以后无论是丢失了几个数字都可以用相同的思路来做
💻第一步:
显而易见,首先利用异或的特性把nums和完整数组异或,得到缺失的两个数的异或结果,即a ^ b
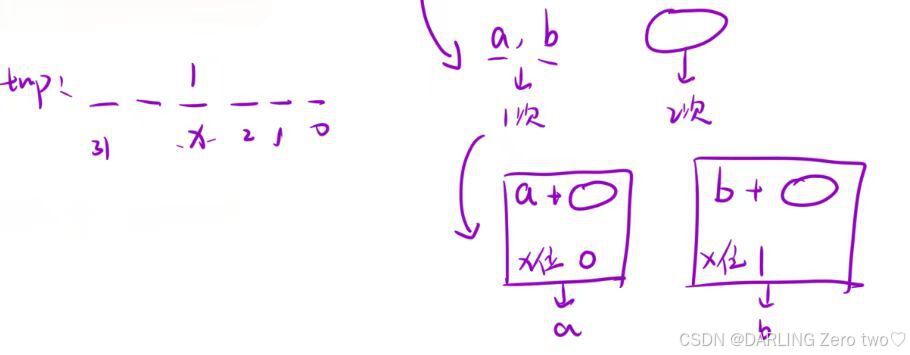
💻第二步:
接下来是最关键的一步,我们要知道除了a、b以外的数在异或时是偶数个,所以能够相互抵消,已知a ^ b = 1,所以两个数异或后为1的那一位,表示在这一位上两个数必然不同,一个数为1,另一个数为0。那么我们就可以根据这个差异,异或后为1有很多位,我们选取最右侧的1来分组方便计算
基于此,我们把最右侧的1这一位定为diff,先把nums进行分类,如果nums在diff位是1,那么就和a异或^ ;如果nums在diff位是0,那么就和b异或^。那么我们现在就是把有差异的那一位和nums异或并分类了,所以我们还要和一个完整的数组分类异或,抵消掉别的数,因为相同异或为0,不同异或为1,由于前面的分类,除了丢失的数,其他的数都抵消了,丢失的数也在异或的过程中把剩余位数补上了
💻代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
vector<int> missingTwo(vector<int>& nums)
{
int ret = 0;
for (auto x : nums)
{
ret ^= x;
}
for (int i = 1; i <= nums.size() + 2; ++i)
{
ret ^= i;
}
int diff = 0;
while (1)
{
if (((ret >> diff) & 1) == 1)
{
break;
}
else
{
diff++;
}
}
int a = 0, b = 0;
for (auto x : nums)
{
if (((x >> diff) & 1) == 1)
{
b ^= x;
}
else
{
a ^= x;
}
}
for (int i = 1; i <= nums.size() + 2; ++i)
{
if (((i >> diff) & 1) == 1)
{
b ^= i;
}
else
{
a ^= i;
}
}
return{ a,b };
}
};