统计问题和数据分析上使用到的抽样分布函数
1. 基本概念和定义
抽样分布也称为统计量分布、随机变量函数分布,是指的是样本估计量的分布。样本估计量是样本的一个函数,在统计中称作统计量,因而抽样分布也是指的是统计量的分布。统计推断是直接基于统计量作出的。一般有两种样本抽样:单一样本统计量和两个样本统计量。多个样本的统计量是基于一个样本抽样形成的,所以下面详细介绍这种抽样。
样本均值抽样分布即所有样本的均值可能取值形成的概率分布。假设总体
X
X
X中个体总数(总体大小)为
N
N
N,样本的容量为
n
(
<
N
)
n(<N)
n(<N)并且总体有限均值为
μ
\mu
μ,方差为
σ
2
\sigma^{2}
σ2,则
E
(
X
ˉ
)
=
E
(
1
n
∑
k
=
1
n
X
k
)
=
1
n
∑
k
=
1
n
E
(
X
k
)
=
1
n
⋅
n
μ
=
μ
\mathbb{E}(\bar X)=\mathbb{E}(\frac{1}{n}\sum\limits_{k=1}^{n}X_{k})=\frac{1}{n}\sum\limits_{k=1}^{n}\mathbb{E}(X_{k})=\frac{1}{n}\cdot n\mu=\mu
E(Xˉ)=E(n1k=1∑nXk)=n1k=1∑nE(Xk)=n1⋅nμ=μ
特别地,当样本为有放回时候,则随机变量
X
i
X_{i}
Xi相互独立,因此有
var
(
X
ˉ
)
=
var
(
1
n
∑
k
=
1
n
X
k
)
=
1
n
2
∑
k
=
1
n
var
(
X
k
)
=
1
n
2
⋅
n
σ
2
=
σ
2
n
\text{var}(\bar X)=\text{var}(\frac{1}{n}\sum\limits_{k=1}^{n}X_{k})=\frac{1}{n^{2}}\sum\limits_{k=1}^{n}\text{var}(X_{k})=\frac{1}{n^{2}}\cdot n\sigma^{2}=\frac{\sigma^{2}}{n}
var(Xˉ)=var(n1k=1∑nXk)=n21k=1∑nvar(Xk)=n21⋅nσ2=nσ2
如果样本为无放回情况的时候,记总体
X
X
X的取值分别为
a
1
,
a
2
,
.
.
.
,
a
N
a_1,a_2,...,a_N
a1,a2,...,aN,由于抽样的随机性质,抽取到任意一个体的概率均为
1
N
\frac{1}{N}
N1,而抽取到任意两个指定个体的概率为
1
N
(
N
−
1
)
\frac{1}{N(N-1)}
N(N−1)1,那么
μ
=
E
(
X
)
=
1
N
∑
k
=
1
N
a
k
=
a
ˉ
\mu= \mathbb{E}(X)=\frac{1}{N}\sum\limits_{k=1}^{N}a_{k}=\bar a
μ=E(X)=N1k=1∑Nak=aˉ
σ 2 = var ( X ) = E ( X − μ ) = 1 N ∑ k = 1 N ( a k − a ˉ ) 2 \sigma^{2}=\text{var}(X)=\mathbb{E}(X-\mu)=\frac{1}{N}\sum\limits_{k=1}^{N}(a_{k}-\bar a)^{2} σ2=var(X)=E(X−μ)=N1k=1∑N(ak−aˉ)2
对于任意的 1 ≤ i ≠ j ≤ n 1\leq i\neq j \leq n 1≤i=j≤n则有
cov ( X i , X j ) = E ( ( X i − μ ) ( X j − μ ) ) = 1 N ( N − 1 ) ∑ s ≠ t ( a t − a ˉ ) ( a t − a ˉ ) = 1 N ( N − 1 ) ⋅ [ ∑ s = 1 N ∑ s = 1 N ( a t − a ˉ ) ( a t − a ˉ ) − ∑ k = 1 N ( a k − a ˉ ) 2 ] \text{cov}(X_{i},X_{j})=\mathbb{E}((X_{i}-\mu)(X_{j}-\mu))\\=\frac{1}{N(N-1)}\sum\limits_{s\neq t}(a_{t}-\bar a)(a_{t}-\bar a)\\=\frac{1}{N(N-1)}\cdot[\sum\limits_{s=1}^{N}\sum\limits_{s=1}^{N}(a_{t}-\bar a)(a_{t}-\bar a)-\sum\limits_{k=1}^{N}(a_{k}-\bar a)^{2}] cov(Xi,Xj)=E((Xi−μ)(Xj−μ))=N(N−1)1s=t∑(at−aˉ)(at−aˉ)=N(N−1)1⋅[s=1∑Ns=1∑N(at−aˉ)(at−aˉ)−k=1∑N(ak−aˉ)2]
注意,
∑
s
=
1
N
∑
s
=
1
N
(
a
t
−
a
ˉ
)
(
a
t
−
a
ˉ
)
=
0
\sum\limits_{s=1}^{N}\sum\limits_{s=1}^{N}(a_{t}-\bar a)(a_{t}-\bar a)=0
s=1∑Ns=1∑N(at−aˉ)(at−aˉ)=0,那么
cov
(
X
i
,
X
j
)
=
−
1
N
(
N
−
1
)
∑
k
=
1
N
(
a
k
−
a
ˉ
)
2
=
−
σ
2
N
−
1
\text{cov}(X_{i},X_{j})=-\frac{1}{N(N-1)}\sum\limits_{k=1}^{N}(a_{k}-\bar a)^{2}=-\frac{\sigma^{2}}{N-1}
cov(Xi,Xj)=−N(N−1)1k=1∑N(ak−aˉ)2=−N−1σ2
从而得到
var
(
X
ˉ
)
=
1
n
2
var
(
∑
k
=
1
n
X
k
)
=
1
n
2
[
∑
k
=
1
n
var
(
X
k
)
+
∑
i
≠
j
cov
(
X
i
,
X
j
)
]
=
1
n
2
[
n
σ
2
−
(
n
2
−
n
)
σ
2
N
−
1
]
=
N
−
n
N
−
1
σ
2
n
\text{var}(\bar X)=\frac{1}{n^{2}}\text{var}(\sum\limits_{k=1}^{n}X_{k})\\=\frac{1}{n^{2}}[\sum\limits_{k=1}^{n}\text{var}(X_{k})+\sum\limits_{i\neq j}\text{cov}(X_{i},X_{j})]\\=\frac{1}{n^{2}}[n\sigma^{2}-\frac{(n^{2}-n)\sigma^{2}}{N-1}]\\=\frac{N-n}{N-1}\frac{\sigma^{2}}{n}
var(Xˉ)=n21var(k=1∑nXk)=n21[k=1∑nvar(Xk)+i=j∑cov(Xi,Xj)]=n21[nσ2−N−1(n2−n)σ2]=N−1N−nnσ2
由上面的两个公式可以看出来,当 n < < N n<<N n<<N的时候,即 n n n比 N N N小得多的时候,两个式子可以近似处理。
2. 常见的抽样分布函数
最基本的由正态分布函数推导出的抽样分布函数,在统计中有三个重要的分布,即 χ 2 \chi^{2} χ2分布, t t t分布和 F F F分布,下面详细推导这量中分布函数。
2.1 正态抽样分布
正态抽样分布是最基本的抽样函数。假随机变量 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,是来自于正态总体 N ( μ , σ 2 ) N(\mu,\sigma^{2}) N(μ,σ2)的样本,并且它们独立同分布、 X k ∼ N ( μ , σ 2 ) X_{k}\sim N(\mu,\sigma^{2}) Xk∼N(μ,σ2)。令 ξ = 1 n ∑ k = 1 n X k \xi=\frac{1}{n}\sum\limits_{k=1}^{n}X_{k} ξ=n1k=1∑nXk,那么显然根据概率分布函数的定义
F ( x ) = P { ξ ≤ x } = 1 ( 2 π σ ) n ∫ . . . ∫ D e x p ( − ∑ k = 1 n ( x k − μ ) 2 2 σ 2 ) d x 1 . . . d x n F(x)=P\{\xi \leq x\}=\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int ...\int_{D}exp({-\frac{\sum\limits_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^2}})dx_{1}...dx_{n} F(x)=P{ξ≤x}=(2πσ)n1∫...∫Dexp(−2σ2k=1∑n(xk−μ)2)dx1...dxn
其中,集合
D
=
{
(
x
1
,
.
.
.
,
x
n
∣
x
1
+
x
2
+
.
.
.
+
x
n
≤
n
x
)
}
D=\{(x_{1},...,x_{n}|x_{1}+x_{2}+...+x_{n}\leq nx)\}
D={(x1,...,xn∣x1+x2+...+xn≤nx)},后者的积分计算方法如下:
实际上,积分空间
D
D
D指的是超平面
x
1
+
x
2
+
.
.
.
+
x
n
≤
n
x
x_{1}+x_{2}+...+x_{n}\leq nx
x1+x2+...+xn≤nx的下方。我们令
x
1
=
u
−
∑
k
=
2
n
x
k
x_{1}=u-\sum\limits_{k=2}^{n}x_{k}
x1=u−k=2∑nxk
那么,后者的积分形式可以写为
F
(
x
)
=
1
(
2
π
σ
)
n
∫
.
.
.
∫
D
e
x
p
(
−
∑
k
=
1
n
(
x
k
−
μ
)
2
2
σ
2
)
d
x
1
.
.
.
d
x
n
=
1
(
2
π
σ
)
n
∫
−
∞
+
∞
.
.
.
∫
−
∞
n
x
−
∑
k
=
2
n
x
k
e
x
p
(
−
∑
k
=
1
n
(
x
k
−
μ
)
2
2
σ
2
)
d
x
1
.
.
.
d
x
n
=
1
(
2
π
σ
)
n
∫
−
∞
+
∞
.
.
.
∫
−
∞
+
∞
∫
−
∞
n
x
e
x
p
(
−
∑
k
=
2
n
(
x
k
−
μ
)
2
+
(
u
−
∑
k
=
2
n
x
k
−
μ
)
2
2
σ
2
)
d
u
d
x
2
.
.
.
d
x
n
=
1
(
2
π
σ
)
n
∫
−
∞
n
x
.
.
.
∫
−
∞
+
∞
∫
−
∞
+
∞
e
x
p
(
−
∑
k
=
2
n
(
x
k
−
μ
)
2
+
(
u
−
∑
k
=
2
n
x
k
−
μ
)
2
2
σ
2
)
d
x
2
.
.
.
d
x
n
d
u
F(x)=\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int ...\int_{D}exp({-\frac{\sum\limits_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^2}})dx_{1}...dx_{n}\\ =\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int_{-\infty}^{+\infty} ...\int_{-\infty}^{nx-\sum\limits_{k=2}^{n}x_{k}}exp({-\frac{\sum\limits_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^2}})dx_{1}...dx_{n}\\ =\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int_{-\infty}^{+\infty} ... \int_{-\infty}^{+\infty}\int_{-\infty}^{nx}exp({-\frac{\sum\limits_{k=2}^{n}(x_{k}-\mu)^{2}+(u-\sum\limits_{k=2}^{n}x_{k}-\mu)^{2}}{2\sigma^2}})dudx_{2}...dx_{n}\\ =\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int_{-\infty}^{nx} ...\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}exp({-\frac{\sum\limits_{k=2}^{n}(x_{k}-\mu)^{2}+(u-\sum\limits_{k=2}^{n}x_{k}-\mu)^{2}}{2\sigma^2}})dx_{2}...dx_{n}du
F(x)=(2πσ)n1∫...∫Dexp(−2σ2k=1∑n(xk−μ)2)dx1...dxn=(2πσ)n1∫−∞+∞...∫−∞nx−k=2∑nxkexp(−2σ2k=1∑n(xk−μ)2)dx1...dxn=(2πσ)n1∫−∞+∞...∫−∞+∞∫−∞nxexp(−2σ2k=2∑n(xk−μ)2+(u−k=2∑nxk−μ)2)dudx2...dxn=(2πσ)n1∫−∞nx...∫−∞+∞∫−∞+∞exp(−2σ2k=2∑n(xk−μ)2+(u−k=2∑nxk−μ)2)dx2...dxndu
为方便计算,对于上式中幂指数
e
x
p
exp
exp中有关项的计算如下:
z
n
=
∑
k
=
2
n
(
x
k
−
μ
)
2
+
(
u
−
∑
k
=
2
n
x
k
−
μ
)
2
=
∑
k
=
2
n
(
x
k
2
−
2
μ
x
k
+
μ
2
)
+
u
2
+
μ
2
+
(
∑
k
=
2
n
x
k
)
2
+
2
μ
∑
k
=
2
n
x
k
−
2
u
∑
k
=
2
n
x
k
−
2
u
μ
=
∑
k
=
2
n
x
k
2
+
(
∑
k
=
2
n
x
k
)
2
−
2
u
∑
k
=
2
n
x
k
+
∑
k
=
2
n
μ
2
+
u
2
+
μ
2
−
2
u
μ
=
∑
k
=
2
n
x
k
2
+
∑
k
=
2
n
∑
j
=
2
n
x
k
x
j
−
2
u
∑
k
=
2
n
x
k
+
n
μ
2
+
u
2
−
2
u
μ
=
2
x
2
2
+
2
x
2
(
∑
k
=
3
n
x
k
−
u
)
+
∑
k
=
3
n
x
k
2
+
∑
k
=
3
n
∑
j
=
3
n
x
k
x
j
−
2
u
∑
k
=
3
n
x
k
+
n
μ
2
+
u
2
−
2
u
μ
=
2
(
x
2
+
∑
k
=
3
n
x
k
−
u
2
)
2
−
(
∑
k
=
3
n
x
k
−
u
)
2
2
+
∑
k
=
3
n
x
k
2
+
∑
k
=
3
n
∑
j
=
3
n
x
k
x
j
−
2
u
∑
k
=
3
n
x
k
+
n
μ
2
+
u
2
−
2
u
μ
=
2
(
x
2
+
∑
k
=
3
n
x
k
−
u
2
)
2
+
∑
k
=
3
n
x
k
2
+
1
2
∑
k
=
3
n
∑
j
=
3
n
x
k
x
j
−
u
∑
k
=
3
n
x
k
+
n
μ
2
+
1
2
u
2
−
2
u
μ
z_{n}=\sum\limits_{k=2}^{n}(x_{k}-\mu)^{2}+(u-\sum\limits_{k=2}^{n}x_{k}-\mu)^{2}\\ =\sum\limits_{k=2}^{n}(x_{k}^{2}-2\mu x_{k}+\mu^{2})+u^{2}+\mu^{2}+(\sum\limits_{k=2}^{n}x_{k})^{2} +2\mu\sum\limits_{k=2}^{n}x_{k}-2u\sum\limits_{k=2}^{n}x_{k}-2u\mu\\ =\sum\limits_{k=2}^{n}x_{k}^{2}+(\sum\limits_{k=2}^{n}x_{k})^{2}-2u\sum\limits_{k=2}^{n}x_{k}+\sum\limits_{k=2}^{n}\mu^{2}+u^{2}+\mu^{2}-2u\mu\\ =\sum\limits_{k=2}^{n}x_{k}^{2}+\sum\limits_{k=2}^{n}\sum\limits_{j=2}^{n}x_{k}x_{j}-2u\sum\limits_{k=2}^{n}x_{k}+n\mu^2+u^{2}-2u\mu\\ =2x_{2}^{2}+2x_{2}(\sum\limits_{k=3}^{n}x_{k}-u)+\sum\limits_{k=3}^{n}x_{k}^{2}+\sum\limits_{k=3}^{n}\sum\limits_{j=3}^{n}x_{k}x_{j}-2u\sum\limits_{k=3}^{n}x_{k}+n\mu^2+u^{2}-2u\mu\\ =2(x_{2}+\frac{\sum\limits_{k=3}^{n}x_{k}-u}{2})^2-\frac{(\sum\limits_{k=3}^{n}x_{k}-u)^2}{2}+\sum\limits_{k=3}^{n}x_{k}^{2}+\sum\limits_{k=3}^{n}\sum\limits_{j=3}^{n}x_{k}x_{j}-2u\sum\limits_{k=3}^{n}x_{k}+n\mu^2+u^{2}-2u\mu\\ =2(x_{2}+\frac{\sum\limits_{k=3}^{n}x_{k}-u}{2})^2+\sum\limits_{k=3}^{n}x_{k}^{2}+\frac{1}{2}\sum\limits_{k=3}^{n}\sum\limits_{j=3}^{n}x_{k}x_{j}-u\sum\limits_{k=3}^{n}x_{k}+n\mu^2+\frac{1}{2}u^{2}-2u\mu
zn=k=2∑n(xk−μ)2+(u−k=2∑nxk−μ)2=k=2∑n(xk2−2μxk+μ2)+u2+μ2+(k=2∑nxk)2+2μk=2∑nxk−2uk=2∑nxk−2uμ=k=2∑nxk2+(k=2∑nxk)2−2uk=2∑nxk+k=2∑nμ2+u2+μ2−2uμ=k=2∑nxk2+k=2∑nj=2∑nxkxj−2uk=2∑nxk+nμ2+u2−2uμ=2x22+2x2(k=3∑nxk−u)+k=3∑nxk2+k=3∑nj=3∑nxkxj−2uk=3∑nxk+nμ2+u2−2uμ=2(x2+2k=3∑nxk−u)2−2(k=3∑nxk−u)2+k=3∑nxk2+k=3∑nj=3∑nxkxj−2uk=3∑nxk+nμ2+u2−2uμ=2(x2+2k=3∑nxk−u)2+k=3∑nxk2+21k=3∑nj=3∑nxkxj−uk=3∑nxk+nμ2+21u2−2uμ
设
c
(
x
2
)
=
2
(
x
2
+
∑
k
=
3
n
x
k
−
u
2
)
2
c(x_{2})=2(x_{2}+\frac{\sum\limits_{k=3}^{n}x_{k}-u}{2})^2
c(x2)=2(x2+2k=3∑nxk−u)2
则
z
n
=
c
(
x
2
)
+
3
2
x
3
2
+
x
3
(
∑
k
=
4
n
x
k
−
u
)
+
∑
k
=
4
n
x
k
2
+
1
2
∑
k
=
4
n
∑
j
=
4
n
x
k
x
j
−
u
∑
k
=
4
n
x
k
+
n
μ
2
+
1
2
u
2
−
2
u
μ
=
c
(
x
2
)
+
3
2
(
x
3
+
∑
k
=
4
n
x
k
−
u
3
)
2
−
1
6
(
∑
k
=
4
n
x
k
−
u
)
2
+
∑
k
=
4
n
x
k
2
+
1
2
∑
k
=
4
n
∑
j
=
4
n
x
k
x
j
−
u
∑
k
=
4
n
x
k
+
n
μ
2
+
1
2
u
2
−
2
u
μ
=
c
(
x
2
)
+
3
2
(
x
3
+
∑
k
=
4
n
x
k
−
u
3
)
2
+
∑
k
=
4
n
x
k
2
+
1
3
∑
k
=
4
n
∑
j
=
4
n
x
k
x
j
−
2
3
u
∑
k
=
4
n
x
k
+
n
μ
2
+
1
3
u
2
−
2
u
μ
z_{n}=c(x_{2})+\frac{3}{2}x_{3}^{2}+x_{3}(\sum\limits_{k=4}^{n}x_{k}-u)+\sum\limits_{k=4}^{n}x_{k}^{2}+\frac{1}{2}\sum\limits_{k=4}^{n}\sum\limits_{j=4}^{n}x_{k}x_{j}-u\sum\limits_{k=4}^{n}x_{k}+n\mu^2+\frac{1}{2}u^{2}-2u\mu\\ =c(x_{2})+\frac{3}{2}(x_{3}+\frac{\sum\limits_{k=4}^{n}x_{k}-u}{3})^2-\frac{1}{6}(\sum\limits_{k=4}^{n}x_{k}-u)^2+\sum\limits_{k=4}^{n}x_{k}^{2}+\frac{1}{2}\sum\limits_{k=4}^{n}\sum\limits_{j=4}^{n}x_{k}x_{j}-u\sum\limits_{k=4}^{n}x_{k}+n\mu^2+\frac{1}{2}u^{2}-2u\mu\\ =c(x_{2})+\frac{3}{2}(x_{3}+\frac{\sum\limits_{k=4}^{n}x_{k}-u}{3})^2+\sum\limits_{k=4}^{n}x_{k}^{2}+\frac{1}{3}\sum\limits_{k=4}^{n}\sum\limits_{j=4}^{n}x_{k}x_{j}-\frac{2}{3}u\sum\limits_{k=4}^{n}x_{k}+n\mu^2+\frac{1}{3}u^{2}-2u\mu
zn=c(x2)+23x32+x3(k=4∑nxk−u)+k=4∑nxk2+21k=4∑nj=4∑nxkxj−uk=4∑nxk+nμ2+21u2−2uμ=c(x2)+23(x3+3k=4∑nxk−u)2−61(k=4∑nxk−u)2+k=4∑nxk2+21k=4∑nj=4∑nxkxj−uk=4∑nxk+nμ2+21u2−2uμ=c(x2)+23(x3+3k=4∑nxk−u)2+k=4∑nxk2+31k=4∑nj=4∑nxkxj−32uk=4∑nxk+nμ2+31u2−2uμ
设
c
(
x
3
)
=
3
2
(
x
3
+
∑
k
=
4
n
x
k
−
u
3
)
2
c(x_{3})=\frac{3}{2}(x_{3}+\frac{\sum\limits_{k=4}^{n}x_{k}-u}{3})^2
c(x3)=23(x3+3k=4∑nxk−u)2
则
z
n
=
c
(
x
2
)
+
c
(
x
3
)
+
∑
k
=
4
n
x
k
2
+
1
3
∑
k
=
4
n
∑
j
=
4
n
x
k
x
j
−
2
3
u
∑
k
=
4
n
x
k
+
n
μ
2
+
1
3
u
2
−
2
u
μ
=
.
.
.
=
c
(
x
2
)
+
c
(
x
3
)
+
.
.
.
+
c
(
x
s
−
1
)
+
∑
k
=
s
n
x
k
2
+
1
s
−
1
∑
k
=
s
n
∑
j
=
s
n
x
k
x
j
−
2
s
−
1
u
∑
k
=
s
n
x
k
+
n
μ
2
+
1
s
−
1
u
2
−
2
u
μ
=
.
.
.
z_{n}=c(x_{2})+c(x_{3})+\sum\limits_{k=4}^{n}x_{k}^{2}+\frac{1}{3}\sum\limits_{k=4}^{n}\sum\limits_{j=4}^{n}x_{k}x_{j}-\frac{2}{3}u\sum\limits_{k=4}^{n}x_{k}+n\mu^2+\frac{1}{3}u^{2}-2u\mu\\ =...\\ =c(x_{2})+c(x_{3})+...+c(x_{s-1})+\sum\limits_{k=s}^{n}x_{k}^{2}+\frac{1}{s-1}\sum\limits_{k=s}^{n}\sum\limits_{j=s}^{n}x_{k}x_{j}-\frac{2}{s-1}u\sum\limits_{k=s}^{n}x_{k}+n\mu^2+\frac{1}{s-1}u^{2}-2u\mu\\ =...
zn=c(x2)+c(x3)+k=4∑nxk2+31k=4∑nj=4∑nxkxj−32uk=4∑nxk+nμ2+31u2−2uμ=...=c(x2)+c(x3)+...+c(xs−1)+k=s∑nxk2+s−11k=s∑nj=s∑nxkxj−s−12uk=s∑nxk+nμ2+s−11u2−2uμ=...
通过一系列计算,可以得到
z n = ∑ k = 2 n c ( x k ) + n μ 2 + u 2 n − 2 u μ z_{n}=\sum\limits_{k=2}^{n}c(x_{k})+n\mu^{2}+\frac{u^{2}}{n}-2u\mu zn=k=2∑nc(xk)+nμ2+nu2−2uμ
其中
c ( x s ) = s s − 1 ( x s + ∑ k = s + 1 n x k − u s ) 2 c(x_{s})=\frac{s}{s-1}(x_{s}+\frac{\sum\limits_{k=s+1}^{n}x_{k}-u}{s})^{2} c(xs)=s−1s(xs+sk=s+1∑nxk−u)2
所以,上述计算过程中积分表达式可以写做
F ( x ) = 1 ( 2 π σ ) n ∫ − ∞ n x e x p ( − n μ 2 + u 2 n − 2 u μ 2 σ 2 ) d u ∫ − ∞ + ∞ c ( x n ) d x n . . . ∫ − ∞ + ∞ c ( x 2 ) d x 2 F(x)=\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\int_{-\infty}^{nx}exp(-\frac{n\mu^{2}+\frac{u^{2}}{n}-2u\mu}{2\sigma^{2}})du\int_{-\infty}^{+\infty}c(x_{n})dx_{n}...\int_{-\infty}^{+\infty}c(x_{2})dx_{2} F(x)=(2πσ)n1∫−∞nxexp(−2σ2nμ2+nu2−2uμ)du∫−∞+∞c(xn)dxn...∫−∞+∞c(x2)dx2
而
∫
−
∞
+
∞
c
(
x
s
)
=
∫
−
∞
+
∞
e
x
p
(
−
s
s
−
1
(
x
s
+
∑
k
=
s
+
1
n
x
k
−
u
s
)
2
2
σ
2
)
d
x
s
=
2
π
σ
⋅
s
−
1
s
\int_{-\infty}^{+\infty}c(x_{s})=\int_{-\infty}^{+\infty}exp(-\frac{\frac{s}{s-1}(x_{s}+\frac{\sum\limits_{k=s+1}^{n}x_{k}-u}{s})^{2}}{2\sigma^{2}})dx_{s}\\ =\sqrt{2\pi}\sigma\cdot\sqrt{\frac{s-1}{s}}
∫−∞+∞c(xs)=∫−∞+∞exp(−2σ2s−1s(xs+sk=s+1∑nxk−u)2)dxs=2πσ⋅ss−1
故而
F ( x ) = 1 ( 2 π σ ) n ⋅ ( 2 π σ ) n − 1 ⋅ n − 1 n ⋅ . . . ⋅ s − 1 s ⋅ . . . ⋅ 2 − 1 2 ∫ − ∞ n x e x p ( − n μ 2 + u 2 n − 2 u μ 2 σ 2 ) d u F(x)=\frac{1}{(\sqrt{2\pi}\sigma)^{n}}\cdot(\sqrt{2\pi}\sigma)^{n-1}\cdot\sqrt{\frac{n-1}{n}}\cdot...\cdot\sqrt{\frac{s-1}{s}}\cdot...\cdot\sqrt{\frac{2-1}{2}}\int_{-\infty}^{nx}exp(-\frac{n\mu^{2}+\frac{u^{2}}{n}-2u\mu}{2\sigma^{2}})du F(x)=(2πσ)n1⋅(2πσ)n−1⋅nn−1⋅...⋅ss−1⋅...⋅22−1∫−∞nxexp(−2σ2nμ2+nu2−2uμ)du
即
F ( x ) = 1 2 π n σ ∫ − ∞ n x e x p ( − 1 n ( u − n μ ) 2 2 σ 2 ) d u F(x)=\frac{1}{\sqrt{2\pi n}\sigma}\int_{-\infty}^{nx}exp(-\frac{\frac{1}{n}(u-n\mu)^{2}}{2\sigma^{2}})du F(x)=2πnσ1∫−∞nxexp(−2σ2n1(u−nμ)2)du
进行变换之后得到
F ( x ) = n 2 π 1 σ ∫ − ∞ x e x p ( − n ( t − μ ) 2 2 σ 2 ) d t F(x)=\sqrt{\frac{n}{2\pi}}\frac{1}{\sigma}\int_{-\infty}^{x}exp(-\frac{n(t-\mu)^{2}}{2\sigma^{2}})dt F(x)=2πnσ1∫−∞xexp(−2σ2n(t−μ)2)dt
所以综上所述, ξ ∼ N ( μ , σ 2 n ) \xi\sim N(\mu,\frac{\sigma^2}{n}) ξ∼N(μ,nσ2),并且有以下的结论
E ( X ˉ ) = μ \mathbb{E}(\bar X)=\mu E(Xˉ)=μ
var ( X ˉ ) = σ 2 n \text{var}(\bar X)=\frac{\sigma^{2}}{n} var(Xˉ)=nσ2
2.2 χ 2 \chi^{2} χ2分布
设
n
n
n个互相独立的随机变量
X
1
,
.
.
.
,
X
n
X_{1},...,X_{n}
X1,...,Xn均服从标准正态分布,则这
n
n
n个服从标准正态分布的随机变量的平方和构成一个新的随机变量
ξ
=
∑
k
=
1
n
X
k
2
\xi=\sum\limits_{k=1}^{n}X_{k}^{2}
ξ=k=1∑nXk2,则称变量
ξ
\xi
ξ服从参数为
n
n
n的卡方分布,并记做
ξ
∼
χ
2
(
n
)
\xi\sim\chi^{2}(n)
ξ∼χ2(n),参数
n
n
n一般称为
χ
2
\chi^2
χ2分布的自由度。
其中均值
E
(
ξ
)
=
E
(
∑
k
=
1
n
X
k
2
)
=
∑
k
=
1
n
E
(
X
k
2
)
\mathbb{E}(\xi)=\mathbb{E}(\sum\limits_{k=1}^{n}X_{k}^{2})=\sum\limits_{k=1}^{n}\mathbb{E}(X_{k}^{2})
E(ξ)=E(k=1∑nXk2)=k=1∑nE(Xk2)
而
E ( X k 2 ) = var ( X k ) + ( E ( X k ) ) 2 = 1 + 0 2 = 1 \mathbb{E}(X_{k}^{2})=\text{var}(X_{k})+(\mathbb{E}(X_{k}))^{2}=1+0^{2}=1 E(Xk2)=var(Xk)+(E(Xk))2=1+02=1
从而得到
E ( ξ ) = n \mathbb{E}(\xi)=n E(ξ)=n
方差的求法如下所示:
var
(
ξ
)
=
E
(
ξ
2
)
−
(
E
(
ξ
)
)
2
\text{var}(\xi)=\mathbb{E}(\xi^{2})-(\mathbb{E}(\xi))^{2}
var(ξ)=E(ξ2)−(E(ξ))2
而
E ( ξ 2 ) = E ( ( ∑ k = 1 n X k 2 ) 2 ) = E ( ∑ k = 1 n ∑ j = 1 n X k 2 X j 2 ) = ∑ k = 1 n E ( X k 4 ) + 2 ∑ k = 1 n ∑ j = 1 k − 1 E ( X k 2 ) E ( X j 2 ) = ∑ k = 1 n E ( X k 4 ) + n ( n − 1 ) \mathbb{E}(\xi^{2})=\mathbb{E}((\sum\limits_{k=1}^{n}X_{k}^{2})^{2})\\ =\mathbb{E}(\sum\limits_{k=1}^{n}\sum\limits_{j=1}^{n}X_{k}^{2}X_{j}^{2})\\ =\sum\limits_{k=1}^{n}\mathbb{E}(X_{k}^{4})+2\sum\limits_{k=1}^{n}\sum\limits_{j=1}^{k-1}\mathbb{E}(X_{k}^{2})\mathbb{E}(X_{j}^{2})\\ =\sum\limits_{k=1}^{n}\mathbb{E}(X_{k}^{4})+n(n-1) E(ξ2)=E((k=1∑nXk2)2)=E(k=1∑nj=1∑nXk2Xj2)=k=1∑nE(Xk4)+2k=1∑nj=1∑k−1E(Xk2)E(Xj2)=k=1∑nE(Xk4)+n(n−1)
E ( X k 4 ) = 1 2 π ∫ − ∞ + ∞ x 4 e − 1 2 x 2 d x = 3 \mathbb{E}(X_{k}^{4})=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}x^{4}e^{-\frac{1}{2}x^{2}}dx=3 E(Xk4)=2π1∫−∞+∞x4e−21x2dx=3
所以
var
(
ξ
)
=
3
n
+
n
(
n
−
1
)
−
n
2
=
2
n
\text{var}(\xi)=3n+n(n-1)-n^{2}=2n
var(ξ)=3n+n(n−1)−n2=2n
χ
2
\chi^{2}
χ2分布是具有可加性的。假设
χ
1
2
∼
χ
2
(
n
)
\chi_{1}^{2}\sim{\chi^{2}(n)}
χ12∼χ2(n)、
χ
2
2
∼
χ
2
(
m
)
\chi_{2}^{2}\sim{\chi^{2}(m)}
χ22∼χ2(m)并且两个随机变量独立,那么根据
χ
2
\chi^{2}
χ2分布的定义可知。
χ
1
2
=
∑
k
=
1
n
X
k
2
\chi_{1}^{2}=\sum\limits_{k=1}^{n}X_{k}^{2}
χ12=k=1∑nXk2
χ 2 2 = ∑ k = 1 m X k 2 \chi_{2}^{2}=\sum\limits_{k=1}^{m}X_{k}^{2} χ22=k=1∑mXk2
可见
χ 1 2 + χ 2 2 = ∑ k = 1 m + n X k 2 \chi_{1}^{2}+\chi_{2}^{2}=\sum\limits_{k=1}^{m+n}X_{k}^{2} χ12+χ22=k=1∑m+nXk2
显然有下面的结论
χ 1 2 + χ 2 2 ∼ χ 2 ( m + n ) \chi_{1}^{2}+\chi_{2}^{2}\sim{\chi^{2}(m+n)} χ12+χ22∼χ2(m+n)
对于 N N N个独立同分布的 χ 2 \chi^{2} χ2分布随机变量之和的分布也是 χ 2 \chi^{2} χ2分布。
χ
2
\chi^2
χ2分布的概率分布函数求法如下所示:
我们首先计算
P
{
ξ
<
x
}
P\{\xi< x\}
P{ξ<x}。当
x
≤
0
x\leq0
x≤0时,显然概率为
0
0
0。当
x
>
0
x>0
x>0时,根据概率分布函数的定义可以得到:
F
(
x
)
=
P
{
ξ
≤
x
}
=
1
(
2
π
)
n
∫
.
.
.
∫
D
e
x
p
(
−
1
2
∑
k
=
1
n
x
k
2
)
d
x
1
.
.
.
d
x
n
F(x)=P\{\xi\leq x\}=\frac{1}{(\sqrt{2\pi})^{n}}\int...\int_{D}exp(-\frac{1}{2}\sum\limits_{k=1}^{n}x_{k}^{2})dx_{1}...dx_{n}
F(x)=P{ξ≤x}=(2π)n1∫...∫Dexp(−21k=1∑nxk2)dx1...dxn
其中,集合区间
D
D
D表示
n
n
n维空间下的球体
D
=
{
(
x
1
,
x
2
,
.
.
.
,
x
n
)
∣
∑
k
=
1
n
x
k
2
≤
x
}
D=\{(x_{1},x_{2},...,x_{n})|\sum\limits_{k=1}^{n}x_{k}^{2}\leq x\}
D={(x1,x2,...,xn)∣k=1∑nxk2≤x},利用球坐标变换公式
x
1
=
r
cos
(
θ
1
)
x_{1}=r\cos(\theta_{1})
x1=rcos(θ1)
x 2 = r sin ( θ 1 ) cos ( θ 2 ) x_{2}=r\sin(\theta_{1})\cos(\theta_{2}) x2=rsin(θ1)cos(θ2)
x 3 = r sin ( θ 1 ) sin ( θ 2 ) cos ( θ 3 ) x_{3}=r\sin(\theta_{1})\sin(\theta_{2})\cos(\theta_{3}) x3=rsin(θ1)sin(θ2)cos(θ3)
. . . ... ...
x n − 1 = r sin ( θ 1 ) sin ( θ 2 ) . . . cos ( θ n − 1 ) x_{n-1}=r\sin(\theta_{1})\sin(\theta_{2})...\cos(\theta_{n-1}) xn−1=rsin(θ1)sin(θ2)...cos(θn−1)
x n = r sin ( θ 1 ) sin ( θ 2 ) . . . sin ( θ n − 1 ) x_{n}=r\sin(\theta_{1})\sin(\theta_{2})...\sin(\theta_{n-1}) xn=rsin(θ1)sin(θ2)...sin(θn−1)
经过推导,可以得到
Jacobi
\text{Jacobi}
Jacobi行列式的结果:
J
=
∂
(
x
1
,
.
.
.
,
x
n
)
∂
(
θ
1
,
.
.
.
,
θ
n
)
=
r
n
−
1
sin
n
−
2
(
θ
1
)
sin
n
−
3
(
θ
2
)
.
.
.
sin
2
(
θ
n
−
3
)
sin
(
θ
n
−
2
)
J=\frac{\partial(x_{1},...,x_{n})}{\partial(\theta_{1},...,\theta_{n})}=r^{n-1}\sin^{n-2}(\theta_{1})\sin^{n-3}(\theta_{2})...\sin^{2}(\theta_{n-3})\sin(\theta_{n-2})
J=∂(θ1,...,θn)∂(x1,...,xn)=rn−1sinn−2(θ1)sinn−3(θ2)...sin2(θn−3)sin(θn−2)
从而得到
F
(
x
)
=
P
{
ξ
≤
x
}
=
1
(
2
π
)
n
∫
0
2
π
sin
n
−
2
(
θ
1
)
d
θ
1
∫
0
2
π
sin
n
−
3
(
θ
2
)
d
θ
2
.
.
.
∫
0
2
π
sin
(
θ
n
−
2
)
d
θ
n
−
2
∫
0
x
e
x
p
(
−
1
2
r
2
)
r
n
−
1
d
r
F(x)=P\{\xi\leq x\}=\frac{1}{(\sqrt{2\pi})^{n}}\int_{0}^{2\pi}\sin^{n-2}(\theta_{1})d\theta_{1}\int_{0}^{2\pi}\sin^{n-3}(\theta_{2})d\theta_{2}...\int_{0}^{2\pi}\sin(\theta_{n-2})d\theta_{n-2}\int_{0}^{\sqrt{x}}exp(-\frac{1}{2}r^{2})r^{n-1}dr
F(x)=P{ξ≤x}=(2π)n1∫02πsinn−2(θ1)dθ1∫02πsinn−3(θ2)dθ2...∫02πsin(θn−2)dθn−2∫0xexp(−21r2)rn−1dr
当然,上式的求法可以通过Wallis公式可以求出值,这里使用一种较为简单的方法。我们令
c
n
=
1
(
2
π
)
n
∫
0
2
π
sin
n
−
2
(
θ
1
)
d
θ
1
∫
0
2
π
sin
n
−
3
(
θ
2
)
d
θ
2
.
.
.
∫
0
2
π
sin
(
θ
n
−
2
)
d
θ
n
−
2
c_{n}=\frac{1}{(\sqrt{2\pi})^{n}}\int_{0}^{2\pi}\sin^{n-2}(\theta_{1})d\theta_{1}\int_{0}^{2\pi}\sin^{n-3}(\theta_{2})d\theta_{2}...\int_{0}^{2\pi}\sin(\theta_{n-2})d\theta_{n-2}
cn=(2π)n1∫02πsinn−2(θ1)dθ1∫02πsinn−3(θ2)dθ2...∫02πsin(θn−2)dθn−2
那么概率分布函数可以化为
F
(
x
)
=
c
n
∫
0
x
e
−
1
2
r
2
r
n
−
1
d
r
F(x)=c_{n}\int_{0}^{\sqrt{x}}e^{-\frac{1}{2}r^{2}}r^{n-1}dr
F(x)=cn∫0xe−21r2rn−1dr
根据概率分布函数的性质,可以得到
lim
x
→
+
∞
F
(
x
)
=
c
n
∫
0
+
∞
e
−
1
2
r
2
r
n
−
1
d
r
=
1
\lim_{x\rightarrow+\infty}F(x)=c_{n}\int_{0}^{+\infty}e^{-\frac{1}{2}r^{2}}r^{n-1}dr=1
x→+∞limF(x)=cn∫0+∞e−21r2rn−1dr=1
再做变换 r = 2 t , d r = d t 2 t r=\sqrt{2t},dr=\frac{dt}{\sqrt{2t}} r=2t,dr=2tdt,那么上式化为
c n ∫ 0 + ∞ e − t ⋅ t n − 2 2 ⋅ 2 n − 2 2 d t = 1 c_{n}\int_{0}^{+\infty}e^{-t}\cdot t^{\frac{n-2}{2}}\cdot 2^{\frac{n-2}{2}}dt=1 cn∫0+∞e−t⋅t2n−2⋅22n−2dt=1
即
c n = 2 1 − n 2 ∫ 0 + ∞ t n − 2 2 e − t d t = 2 1 − n 2 Γ ( n 2 ) c_{n}=\frac{2^{1-\frac{n}{2}}}{\int_{0}^{+\infty}t^{\frac{n-2}{2}}e^{-t}dt}=\frac{2^{1-\frac{n}{2}}}{\Gamma(\frac{n}{2})} cn=∫0+∞t2n−2e−tdt21−2n=Γ(2n)21−2n
所以得到
F ( x ) = 2 1 − n 2 Γ ( n 2 ) ∫ 0 x e − 1 2 r 2 r n − 1 d r = 2 − n 2 Γ ( n 2 ) ∫ 0 x e − 1 2 t t n 2 − 1 d t F(x)=\frac{2^{1-\frac{n}{2}}}{\Gamma(\frac{n}{2})}\int_{0}^{\sqrt x}e^{-\frac{1}{2}r^{2}}r^{n-1}dr\\ =\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}\int_{0}^{x}e^{-\frac{1}{2}t}t^{\frac{n}{2}-1}dt F(x)=Γ(2n)21−2n∫0xe−21r2rn−1dr=Γ(2n)2−2n∫0xe−21tt2n−1dt
综上所述, χ 2 \chi^{2} χ2分布概率密度函数为
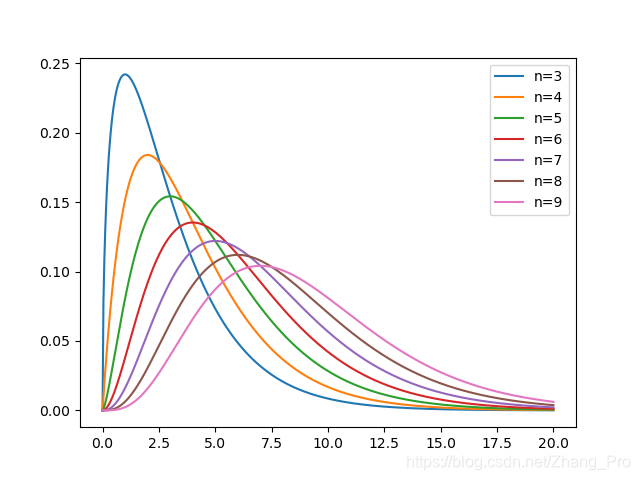
f ( x ∣ n ) = { 2 − n 2 Γ ( n 2 ) e − 1 2 x x n 2 − 1 , if x > 0 0 , if x ≤ 0 f(x|n)=\begin{cases} \frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}e^{-\frac{1}{2}x}x^{\frac{n}{2}-1} &, \text{ if } x>0\\ 0&,\text{ if } x\leq 0 \end{cases} f(x∣n)={Γ(2n)2−2ne−21xx2n−10, if x>0, if x≤0
χ
2
\chi^{2}
χ2分布的函数图像如下所示
实际上, χ 2 \chi^{2} χ2分布是 Gamma \text{Gamma} Gamma分布的一种特殊情况。特别地,若随机变量 X X X满足 X ∼ χ 2 ( n ) X\sim \chi^{2}(n) X∼χ2(n),那么必然有 X ∼ Gam ( n 2 , 1 2 ) X\sim\text{Gam}(\frac{n}{2},\frac{1}{2}) X∼Gam(2n,21)。具体 Gamma \text{Gamma} Gamma分布函数可以参考笔者的另一篇博文:深度学习中的一些概率函数分布。
2.3 t分布
若随机变量
X
X
X和
Y
Y
Y相互独立,并且
X
∼
N
(
0
,
1
)
,
Y
∼
χ
2
(
n
)
X\sim N(0,1),Y\sim \chi^{2}(n)
X∼N(0,1),Y∼χ2(n),称随机变量
T
=
X
Y
/
n
T=\frac{X}{\sqrt{Y/n}}
T=Y/nX
为自由度为
n
n
n的
t
t
t分布,并记做
T
∼
t
(
n
)
T\sim t(n)
T∼t(n)。
t
t
t分布概率密度函数推导过程如下所示:
设
t
t
t概率分布函数为
F
(
t
)
F(t)
F(t),那么根据概率分布函数的定义得到:
F
(
t
)
=
P
{
T
≤
t
}
=
P
{
X
Y
/
n
≤
t
}
=
P
{
X
≤
t
⋅
Y
/
n
}
=
∫
−
∞
+
∞
(
∫
−
∞
t
y
n
f
X
(
x
)
d
x
)
f
Y
(
y
)
d
y
=
∫
0
+
∞
∫
−
∞
t
y
n
1
2
π
e
−
1
2
x
2
⋅
2
−
n
2
Γ
(
n
2
)
⋅
e
−
1
2
y
y
n
2
−
1
d
x
d
y
=
1
2
π
⋅
2
−
n
2
Γ
(
n
2
)
∫
0
+
∞
∫
−
∞
t
y
n
e
−
x
2
+
y
2
y
n
2
−
1
d
x
d
y
F(t)=P\{T\leq{t}\}=P\{\frac{X}{\sqrt{Y/n}}\leq{t}\}=P\{X\leq{t}\cdot{\sqrt{Y/n}}\}\\ =\int_{-\infty}^{+\infty}(\int_{-\infty}^{t\sqrt{\frac{y}{n}}}f_{X}(x)dx)f_{Y}(y)dy\\ =\int_{0}^{+\infty}\int_{-\infty}^{t\sqrt{\frac{y}{n}}}\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\cdot{e^{-\frac{1}{2}y}y^{\frac{n}{2}-1}}dxdy\\ =\frac{1}{\sqrt{2\pi}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{0}^{+\infty}\int_{-\infty}^{t\sqrt{\frac{y}{n}}}e^{-\frac{x^{2}+y}{2}}y^{\frac{n}{2}-1}dxdy
F(t)=P{T≤t}=P{Y/nX≤t}=P{X≤t⋅Y/n}=∫−∞+∞(∫−∞tnyfX(x)dx)fY(y)dy=∫0+∞∫−∞tny2π1e−21x2⋅Γ(2n)2−2n⋅e−21yy2n−1dxdy=2π1⋅Γ(2n)2−2n∫0+∞∫−∞tnye−2x2+yy2n−1dxdy
做变换 u = x n y u=x\sqrt{\frac{n}{y}} u=xyn,则 d u = n y d x , d x = y n d u du=\sqrt{\frac{n}{y}}dx,dx=\sqrt{\frac{y}{n}}du du=yndx,dx=nydu, x = u y n x=u\sqrt{\frac{y}{n}} x=uny,所以积分表达式变为
F ( t ) = 1 2 π ⋅ 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ ∫ − ∞ t e − y u 2 + n y 2 n y n 2 − 1 y n d u d y = 1 2 π n ⋅ 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ ∫ − ∞ t e − y u 2 + n y 2 n y n − 1 2 d u d y F(t)=\frac{1}{\sqrt{2\pi}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{0}^{+\infty}\int_{-\infty}^{t}e^{-\frac{yu^{2}+ny}{2n}}y^{\frac{n}{2}-1}\sqrt{\frac{y}{n}}dudy\\ =\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{0}^{+\infty}\int_{-\infty}^{t}e^{-\frac{yu^{2}+ny}{2n}}y^{\frac{n-1}{2}}dudy F(t)=2π1⋅Γ(2n)2−2n∫0+∞∫−∞te−2nyu2+nyy2n−1nydudy=2πn1⋅Γ(2n)2−2n∫0+∞∫−∞te−2nyu2+nyy2n−1dudy
所以,有以下的表达式
F
(
t
)
=
1
2
π
n
⋅
2
−
n
2
Γ
(
n
2
)
∫
−
∞
t
∫
0
+
∞
e
−
y
u
2
+
n
y
2
n
y
n
−
1
2
d
y
d
u
F(t)=\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{-\infty}^{t}\int_{0}^{+\infty}e^{-\frac{yu^{2}+ny}{2n}}y^{\frac{n-1}{2}}dydu
F(t)=2πn1⋅Γ(2n)2−2n∫−∞t∫0+∞e−2nyu2+nyy2n−1dydu
从而有
f
(
t
)
=
d
F
(
t
)
d
t
=
1
2
π
n
⋅
2
−
n
2
Γ
(
n
2
)
∫
0
+
∞
e
−
y
t
2
+
n
y
2
n
y
n
−
1
2
d
y
f(t)=\frac{dF(t)}{dt}=\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{0}^{+\infty}e^{-\frac{yt^{2}+ny}{2n}}y^{\frac{n-1}{2}}dy
f(t)=dtdF(t)=2πn1⋅Γ(2n)2−2n∫0+∞e−2nyt2+nyy2n−1dy
做变换 z = t 2 + n 2 n y , y = 2 n t 2 + n z z=\frac{t^{2}+n}{2n}y,y=\frac{2n}{t^{2}+n}z z=2nt2+ny,y=t2+n2nz,那么 d z = t 2 + n 2 n d y , d y = 2 n t 2 + n d z dz=\frac{t^{2}+n}{2n}dy,dy=\frac{2n}{t^{2}+n}dz dz=2nt2+ndy,dy=t2+n2ndz,所以有
f ( t ) = 1 2 π n ⋅ 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ e − z ( 2 n t 2 + n z ) n − 1 2 ⋅ 2 n t 2 + n d z = 1 2 π n ⋅ 2 − n 2 Γ ( n 2 ) ( 2 n t 2 + n ) n + 1 2 ∫ 0 + ∞ e − z z n − 1 2 d z = 1 2 π n ⋅ 2 − n 2 Γ ( n 2 ) ⋅ ( t 2 + n 2 n ) − n + 1 2 ⋅ Γ ( n + 1 2 ) = Γ ( n + 1 2 ) Γ ( n 2 ) ⋅ 1 n π ( t 2 n + 1 ) − n + 1 2 f(t)=\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\int_{0}^{+\infty}e^{-z}(\frac{2n}{t^{2}+n}z)^{\frac{n-1}{2}}\cdot{\frac{2n}{t^{2}+n}}dz\\ =\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}(\frac{2n}{t^{2}+n})^{\frac{n+1}{2}}\int_{0}^{+\infty}e^{-z}z^{\frac{n-1}{2}}dz\\ =\frac{1}{\sqrt{2\pi n}}\cdot{\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}}\cdot{(\frac{t^{2}+n}{2n})^{-\frac{n+1}{2}}}\cdot{\Gamma(\frac{n+1}{2})}\\ =\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\cdot{\frac{1}{\sqrt{n\pi}}}(\frac{t^{2}}{n}+1)^{-\frac{n+1}{2}} f(t)=2πn1⋅Γ(2n)2−2n∫0+∞e−z(t2+n2nz)2n−1⋅t2+n2ndz=2πn1⋅Γ(2n)2−2n(t2+n2n)2n+1∫0+∞e−zz2n−1dz=2πn1⋅Γ(2n)2−2n⋅(2nt2+n)−2n+1⋅Γ(2n+1)=Γ(2n)Γ(2n+1)⋅nπ1(nt2+1)−2n+1
这样我们得到了t分布的表达式
Stu ( x ∣ n ) = Γ ( n + 1 2 ) Γ ( n 2 ) ⋅ 1 n π ( x 2 n + 1 ) − n + 1 2 \text{Stu}(x|n)=\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\cdot{\frac{1}{\sqrt{n\pi}}}(\frac{x^{2}}{n}+1)^{-\frac{n+1}{2}} Stu(x∣n)=Γ(2n)Γ(2n+1)⋅nπ1(nx2+1)−2n+1
其中均值和方差的推导如下所示:
由于随机变量
X
X
X和
Y
Y
Y相互独立,故而
X
X
X和
n
Y
\sqrt{\frac{n}{Y}}
Yn也是互相独立的,故而
E
(
T
)
=
E
(
X
Y
/
n
)
=
E
(
X
)
E
(
n
Y
)
=
0
⋅
E
(
n
Y
)
=
0
\mathbb{E}(T)=E(\frac{X}{\sqrt{Y/n}})=E(X)E(\sqrt{\frac{n}{Y}})=0\cdot{E(\sqrt{\frac{n}{Y}})}=0
E(T)=E(Y/nX)=E(X)E(Yn)=0⋅E(Yn)=0
var ( T ) = var ( X Y / n ) = E ( n X 2 Y ) − ( E ( X Y / n ) ) 2 = n E ( X 2 ) E ( 1 Y ) \text{var}(T)=\text{var}(\frac{X}{\sqrt{Y/n}})\\ =E(\frac{nX^{2}}{Y})-(E(\frac{X}{\sqrt{Y/n}}))^{2}\\ =nE(X^{2})E(\frac{1}{Y}) var(T)=var(Y/nX)=E(YnX2)−(E(Y/nX))2=nE(X2)E(Y1)
E ( X 2 ) = var ( X ) + ( E ( X ) ) 2 = 1 E(X^{2})=\text{var}(X)+(E(X))^{2}=1 E(X2)=var(X)+(E(X))2=1
E ( 1 Y ) = 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ 1 x e − 1 2 x x n 2 − 1 d x = 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ e − 1 2 x x n 2 − 2 d x E(\frac{1}{Y})=\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}\int_{0}^{+\infty}\frac{1}{x}e^{-\frac{1}{2}x}x^{\frac{n}{2}-1}dx\\ =\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}\int_{0}^{+\infty}e^{-\frac{1}{2}x}x^{\frac{n}{2}-2}dx E(Y1)=Γ(2n)2−2n∫0+∞x1e−21xx2n−1dx=Γ(2n)2−2n∫0+∞e−21xx2n−2dx
做变换 z = x 2 z=\frac{x}{2} z=2x,那么 x = 2 z , d x = 2 d z x=2z,dx=2dz x=2z,dx=2dz,从而得到
E ( 1 Y ) = 2 − n 2 Γ ( n 2 ) ∫ 0 + ∞ e − z ( 2 z ) n 2 − 2 2 d z = 2 − n 2 2 Γ ( n 2 ) ∫ 0 + ∞ e − z z n 2 − 2 d z = 2 − n 2 2 Γ ( n 2 ) ⋅ Γ ( n 2 − 1 ) E(\frac{1}{Y})=\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}\int_{0}^{+\infty}e^{-z}(2z)^{\frac{n}{2}-2}2dz\\ =\frac{2^{-\frac{n}{2}}}{2\Gamma(\frac{n}{2})}\int_{0}^{+\infty}e^{-z}z^{\frac{n}{2}-2}dz\\ =\frac{2^{-\frac{n}{2}}}{2\Gamma(\frac{n}{2})}\cdot{\Gamma(\frac{n}{2}-1)} E(Y1)=Γ(2n)2−2n∫0+∞e−z(2z)2n−22dz=2Γ(2n)2−2n∫0+∞e−zz2n−2dz=2Γ(2n)2−2n⋅Γ(2n−1)
而根据Gamma函数的性质可知
Γ
(
n
2
)
=
(
n
2
−
1
)
Γ
(
n
2
−
1
)
\Gamma(\frac{n}{2})=(\frac{n}{2}-1)\Gamma(\frac{n}{2}-1)
Γ(2n)=(2n−1)Γ(2n−1)
即
Γ ( n 2 − 1 ) Γ ( n 2 ) = 2 n − 2 \frac{\Gamma(\frac{n}{2}-1)}{\Gamma(\frac{n}{2})}=\frac{2}{n-2} Γ(2n)Γ(2n−1)=n−22
所以
E ( 1 Y ) = 1 n − 2 E(\frac{1}{Y})=\frac{1}{n-2} E(Y1)=n−21
所以对于t分布的方差为
var
(
T
)
=
n
n
−
2
\text{var}(T)=\frac{n}{n-2}
var(T)=n−2n
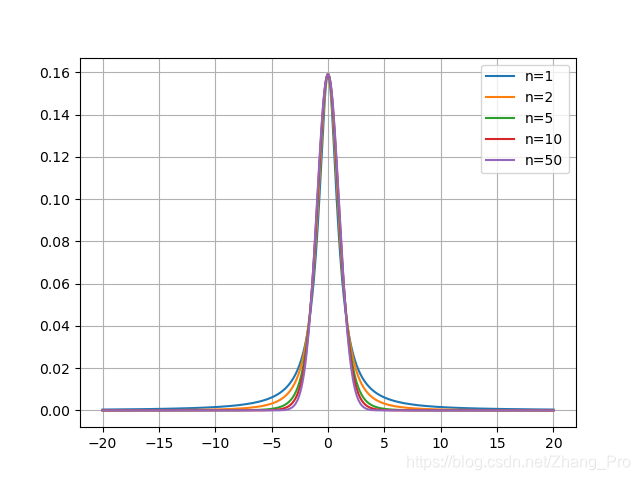
t分布概率密度函数图像如下所示:
自由度 n n n是决定 t t t分布概率密度函数的条件。特别地,当 n → + ∞ n\rightarrow+\infty n→+∞时候, t t t分布近似于正态分布函数。证明如下所示:
lim n → + ∞ Stu ( x ∣ n ) = lim n → + ∞ Γ ( n + 1 2 ) Γ ( n 2 ) ⋅ 1 n π ( x 2 n + 1 ) − n + 1 2 = lim n → + ∞ Γ ( n + 1 2 ) Γ ( n 2 ) ⋅ 1 n π ⋅ lim n → + ∞ ( x 2 n + 1 ) − n + 1 2 \lim_{n\rightarrow+\infty}\text{Stu}(x|n)=\lim_{n\rightarrow+\infty}\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\cdot{\frac{1}{\sqrt{n\pi}}}(\frac{x^{2}}{n}+1)^{-\frac{n+1}{2}}\\ =\lim_{n\rightarrow+\infty}\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\cdot{\frac{1}{\sqrt{n\pi}}}\cdot{\lim_{n\rightarrow+\infty}}(\frac{x^{2}}{n}+1)^{-\frac{n+1}{2}} n→+∞limStu(x∣n)=n→+∞limΓ(2n)Γ(2n+1)⋅nπ1(nx2+1)−2n+1=n→+∞limΓ(2n)Γ(2n+1)⋅nπ1⋅n→+∞lim(nx2+1)−2n+1
其中,
lim
n
→
+
∞
(
x
2
n
+
1
)
−
n
+
1
2
=
e
−
1
2
x
2
\lim_{n\rightarrow+\infty}(\frac{x^{2}}{n}+1)^{-\frac{n+1}{2}}=e^{-\frac{1}{2}x^{2}}
n→+∞lim(nx2+1)−2n+1=e−21x2
对于t分布中的归一化系数
I
n
=
Γ
(
n
+
1
2
)
Γ
(
n
2
)
⋅
1
n
π
I_{n}=\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\cdot{\frac{1}{\sqrt{n\pi}}}
In=Γ(2n)Γ(2n+1)⋅nπ1
极限的计算首先引入两个引理。假设 k k k为整数,那么根据Gamma函数的性质可知:
Γ ( k + 1 2 ) = ( k − 1 2 ) Γ ( k − 1 2 ) = . . . = ( 2 k − 1 ) ! ! 2 k Γ ( 1 2 ) = ( 2 k − 1 ) ! ! 2 k π \Gamma(k+\frac{1}{2})=(k-\frac{1}{2})\Gamma(k-\frac{1}{2})=...=\frac{(2k-1)!!}{2^{k}}\Gamma(\frac{1}{2})=\frac{(2k-1)!!}{2^{k}}\sqrt{\pi} Γ(k+21)=(k−21)Γ(k−21)=...=2k(2k−1)!!Γ(21)=2k(2k−1)!!π
Γ ( k ) = ( k − 1 ) ! Γ ( 1 ) = ( k − 1 ) ! \Gamma(k)=(k-1)!\Gamma(1)=(k-1)! Γ(k)=(k−1)!Γ(1)=(k−1)!
以及Wallis公式:
lim
n
→
+
∞
(
(
2
k
)
!
!
(
2
k
−
1
)
!
!
)
2
1
2
k
+
1
=
π
2
\lim_{n\rightarrow+\infty}(\frac{(2k)!!}{(2k-1)!!})^{2}\frac{1}{2k+1}=\frac{\pi}{2}
n→+∞lim((2k−1)!!(2k)!!)22k+11=2π
有了以上的引理,那么
I
n
I_{n}
In的极限也就很容易求出来了:
所以当
n
n
n为偶数的时候,不妨设
n
=
2
k
n=2k
n=2k,则
lim
k
→
+
∞
I
2
k
=
lim
k
→
+
∞
Γ
(
2
k
+
1
2
)
Γ
(
2
k
2
)
⋅
1
2
k
π
=
lim
k
→
+
∞
(
2
k
−
1
)
!
!
2
k
π
(
k
−
1
)
!
⋅
1
2
k
π
=
lim
k
→
+
∞
(
2
k
−
1
)
!
!
(
2
k
)
!
!
⋅
2
k
2
=
lim
k
→
+
∞
(
2
k
−
1
)
!
!
(
2
k
)
!
!
⋅
2
k
+
1
⋅
2
k
2
2
k
+
1
=
2
π
⋅
1
2
=
1
2
π
\lim_{k\rightarrow+\infty}I_{2k}=\lim_{k\rightarrow+\infty}\frac{\Gamma(\frac{2k+1}{2})}{\Gamma(\frac{2k}{2})}\cdot{\frac{1}{\sqrt{2k\pi}}}\\ =\lim_{k\rightarrow+\infty}\frac{\frac{(2k-1)!!}{2^{k}}\sqrt{\pi}}{(k-1)!}\cdot{\frac{1}{\sqrt{2k\pi}}}\\ =\lim_{k\rightarrow+\infty}\frac{(2k-1)!!}{(2k)!!}\cdot{\frac{\sqrt{2k}}{2}}\\ =\lim_{k\rightarrow+\infty}\frac{(2k-1)!!}{(2k)!!}\cdot{\sqrt{2k+1}}\cdot{\frac{\sqrt{2k}}{2\sqrt{2k+1}}}=\sqrt{\frac{2}{\pi}}\cdot{\frac{1}{2}}=\frac{1}{\sqrt{2\pi}}
k→+∞limI2k=k→+∞limΓ(22k)Γ(22k+1)⋅2kπ1=k→+∞lim(k−1)!2k(2k−1)!!π⋅2kπ1=k→+∞lim(2k)!!(2k−1)!!⋅22k=k→+∞lim(2k)!!(2k−1)!!⋅2k+1⋅22k+12k=π2⋅21=2π1
当
n
n
n为奇数的时候,不妨设
n
=
2
k
+
1
n=2k+1
n=2k+1,则
lim
k
→
+
∞
I
2
k
+
1
=
lim
k
→
+
∞
Γ
(
2
k
+
1
+
1
2
)
Γ
(
2
k
+
1
2
)
⋅
1
(
2
k
+
1
)
π
=
k
!
(
2
k
−
1
)
!
!
2
k
π
⋅
1
(
2
k
+
1
)
π
=
lim
k
→
+
∞
(
2
k
)
!
!
(
2
k
−
1
)
!
!
⋅
1
2
k
+
1
⋅
1
π
=
π
2
⋅
1
π
=
1
2
π
\lim_{k\rightarrow+\infty}I_{2k+1}=\lim_{k\rightarrow+\infty}\frac{\Gamma(\frac{2k+1+1}{2})}{\Gamma(\frac{2k+1}{2})}\cdot{\frac{1}{\sqrt{(2k+1)\pi}}}\\ =\frac{k!}{\frac{(2k-1)!!}{2^{k}}\sqrt{\pi}}\cdot{\frac{1}{\sqrt{(2k+1)\pi}}}\\ =\lim_{k\rightarrow+\infty}\frac{(2k)!!}{(2k-1)!!}\cdot{\frac{1}{\sqrt{2k+1}}}\cdot{\frac{1}{\pi}}\\ =\sqrt{\frac{\pi}{2}}\cdot{\frac{1}{\pi}}=\frac{1}{\sqrt{2\pi}}
k→+∞limI2k+1=k→+∞limΓ(22k+1)Γ(22k+1+1)⋅(2k+1)π1=2k(2k−1)!!πk!⋅(2k+1)π1=k→+∞lim(2k−1)!!(2k)!!⋅2k+11⋅π1=2π⋅π1=2π1
显然
lim
n
→
+
∞
I
n
=
lim
k
→
+
∞
I
2
k
=
lim
k
→
+
∞
I
2
k
+
1
=
1
2
π
\lim\limits_{n\rightarrow+\infty}I_{n}=\lim\limits_{k\rightarrow+\infty}I_{2k}=\lim\limits_{k\rightarrow+\infty}I_{2k+1}=\frac{1}{\sqrt{2\pi}}
n→+∞limIn=k→+∞limI2k=k→+∞limI2k+1=2π1
故而
lim
n
→
+
∞
Stu
(
x
∣
n
)
=
1
2
π
e
−
1
2
x
2
\lim_{n\rightarrow+\infty}\text{Stu}(x|n)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^{2}}
n→+∞limStu(x∣n)=2π1e−21x2
所以有结论
lim
n
→
+
∞
Stu
(
n
)
=
N
(
0
,
1
)
\lim_{n\rightarrow+\infty}\text{Stu}(n)=N(0,1)
n→+∞limStu(n)=N(0,1)
在笔者的一篇博文深度学习中的一些概率函数分布中提到了一种一般形式的t分布函数:
Stu
(
x
∣
μ
,
λ
,
n
)
=
Γ
(
n
+
1
2
)
Γ
(
n
2
)
λ
n
π
(
1
+
λ
(
x
−
μ
)
2
n
)
−
n
+
1
2
\text{Stu}(x|\mu,\lambda,n)=\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})}\sqrt{\frac{\lambda}{n\pi}}(1+\frac{\lambda(x-\mu)^{2}}{n})^{-\frac{n+1}{2}}
Stu(x∣μ,λ,n)=Γ(2n)Γ(2n+1)nπλ(1+nλ(x−μ)2)−2n+1
其函数的极限也是正态分布密度函数,其中精度
λ
=
σ
−
2
\lambda=\sigma^{-2}
λ=σ−2。
lim
n
→
+
∞
Stu
(
x
∣
μ
,
λ
,
n
)
=
λ
2
π
e
−
λ
(
x
−
μ
)
2
2
\lim_{n\rightarrow+\infty}\text{Stu}(x|\mu,\lambda,n)=\sqrt{\frac{\lambda}{2\pi}}e^{-\frac{\lambda(x-\mu)^{2}}{2}}
n→+∞limStu(x∣μ,λ,n)=2πλe−2λ(x−μ)2
2.4 F分布
F分布是抽样分布中最为常见的一种分布方式。若总体
X
∼
N
(
0
,
1
)
X\sim{N(0,1)}
X∼N(0,1),其中两个独立样本
X
1
,
X
2
,
.
.
.
,
X
n
X_{1},X_{2},...,X_{n}
X1,X2,...,Xn和
Y
1
,
Y
2
,
.
.
.
,
Y
m
Y_{1},Y_{2},...,Y_{m}
Y1,Y2,...,Ym为来自总体
X
X
X的样本,设统计量
F
=
1
n
∑
k
=
1
n
X
k
2
1
m
∑
k
=
1
m
Y
k
2
F=\frac{\frac{1}{n}\sum\limits_{k=1}^{n}X_{k}^{2}}{\frac{1}{m}\sum\limits_{k=1}^{m}Y_{k}^{2}}
F=m1k=1∑mYk2n1k=1∑nXk2
则定义统计量
F
F
F服从自由度为
n
,
m
n,m
n,m的
F
F
F分布,并且记为
F
∼
F
(
n
,
m
)
F\sim{F(n,m)}
F∼F(n,m)。当然,
F
F
F分布的定义可以定义为两个
χ
2
\chi^{2}
χ2分布的随机变量的比值的定义,即
F
=
1
n
χ
2
(
n
)
1
m
χ
2
(
m
)
F=\frac{\frac{1}{n}\chi^2(n)}{\frac{1}{m}\chi^2(m)}
F=m1χ2(m)n1χ2(n)
其中概率密度函数的推导如下所示:
F
(
t
)
=
P
{
F
≤
t
}
=
P
{
m
n
⋅
X
Y
≤
t
}
F(t)=P\{F\leq{t}\}=P\{\frac{m}{n}\cdot{\frac{X}{Y}}\leq{t}\}
F(t)=P{F≤t}=P{nm⋅YX≤t}
当
t
<
0
t<0
t<0时候,显然
F
(
t
)
=
P
{
F
≤
t
}
=
0
F(t)=P\{F\leq{t}\}=0
F(t)=P{F≤t}=0
当 t ≥ 0 t\geq{0} t≥0时候,那么
F ( t ) = P { F ≤ t } = P { m n ⋅ X Y ≤ t } = P { X ≤ n t m Y } = ∫ − ∞ + ∞ ( ∫ − ∞ n t m y f X ( x ) d x ) f Y ( y ) d y = ∫ 0 + ∞ ∫ 0 n t m y 2 − n 2 Γ ( n 2 ) e − 1 2 x x n 2 − 1 2 − m 2 Γ ( m 2 ) e − 1 2 y y m 2 − 1 d x d y = 2 − n + m 2 Γ ( n 2 ) Γ ( m 2 ) ∫ 0 + ∞ ∫ 0 n t m y e − 1 2 ( x + y ) x n 2 − 1 y m 2 − 1 d x d y F(t)=P\{F\leq{t}\}=P\{\frac{m}{n}\cdot{\frac{X}{Y}}\leq{t}\}\\ =P\{X\leq{\frac{nt}{m}Y}\}\\ =\int_{-\infty}^{+\infty}(\int_{-\infty}^{\frac{nt}{m}y}f_{X}(x)dx)f_{Y}(y)dy\\ =\int_{0}^{+\infty}\int_{0}^{\frac{nt}{m}y}\frac{2^{-\frac{n}{2}}}{\Gamma(\frac{n}{2})}e^{-\frac{1}{2}x}x^{\frac{n}{2}-1}\frac{2^{-\frac{m}{2}}}{\Gamma(\frac{m}{2})}e^{-\frac{1}{2}y}y^{\frac{m}{2}-1}dxdy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\int_{0}^{+\infty}\int_{0}^{\frac{nt}{m}y}e^{-\frac{1}{2}(x+y)}x^{\frac{n}{2}-1}y^{\frac{m}{2}-1}dxdy F(t)=P{F≤t}=P{nm⋅YX≤t}=P{X≤mntY}=∫−∞+∞(∫−∞mntyfX(x)dx)fY(y)dy=∫0+∞∫0mntyΓ(2n)2−2ne−21xx2n−1Γ(2m)2−2me−21yy2m−1dxdy=Γ(2n)Γ(2m)2−2n+m∫0+∞∫0mntye−21(x+y)x2n−1y2m−1dxdy
现在,令
u
=
m
x
n
y
u=\frac{mx}{ny}
u=nymx,那么
d
u
=
m
n
y
d
x
du=\frac{m}{ny}dx
du=nymdx即
d
x
=
n
y
m
d
u
dx=\frac{ny}{m}du
dx=mnydu,
x
=
n
y
m
u
x=\frac{ny}{m}u
x=mnyu,故而可以得到
F
(
t
)
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
∫
0
+
∞
∫
0
t
n
y
m
⋅
e
−
n
y
2
m
u
e
−
1
2
y
(
n
y
m
u
)
n
2
−
1
y
m
2
−
1
d
u
d
y
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
∫
0
+
∞
∫
0
t
y
⋅
e
−
n
y
2
m
u
⋅
e
−
1
2
y
⋅
(
y
u
)
n
2
−
1
⋅
y
m
2
−
1
d
u
d
y
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
∫
0
+
∞
∫
0
t
e
−
n
y
2
m
u
e
−
1
2
y
u
n
2
−
1
y
m
+
n
2
−
1
d
u
d
y
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
∫
0
t
∫
0
+
∞
e
−
n
y
2
m
u
e
−
1
2
y
u
n
2
−
1
y
m
+
n
2
−
1
d
y
d
u
F(t)=\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\int_{0}^{+\infty}\int_{0}^{t}\frac{ny}{m}\cdot{e^{-\frac{ny}{2m}u}e^{-\frac{1}{2}y}(\frac{ny}{m}u)^{\frac{n}{2}-1}y^{\frac{m}{2}-1}}dudy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}\int_{0}^{+\infty}\int_{0}^{t}y\cdot{e^{-\frac{ny}{2m}u}}\cdot{e^{-\frac{1}{2}y}}\cdot{(yu)^{\frac{n}{2}-1}}\cdot{y^{\frac{m}{2}-1}}dudy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}\int_{0}^{+\infty}\int_{0}^{t}e^{-\frac{ny}{2m}u}e^{-\frac{1}{2}y}u^{\frac{n}{2}-1}y^{\frac{m+n}{2}-1}dudy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}\int_{0}^{t}\int_{0}^{+\infty}e^{-\frac{ny}{2m}u}e^{-\frac{1}{2}y}u^{\frac{n}{2}-1}y^{\frac{m+n}{2}-1}dydu
F(t)=Γ(2n)Γ(2m)2−2n+m∫0+∞∫0tmny⋅e−2mnyue−21y(mnyu)2n−1y2m−1dudy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2n∫0+∞∫0ty⋅e−2mnyu⋅e−21y⋅(yu)2n−1⋅y2m−1dudy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2n∫0+∞∫0te−2mnyue−21yu2n−1y2m+n−1dudy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2n∫0t∫0+∞e−2mnyue−21yu2n−1y2m+n−1dydu
所以
f
(
t
)
=
d
F
(
t
)
d
t
=
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
∫
0
+
∞
e
−
n
y
2
m
t
e
−
1
2
y
t
n
2
−
1
y
m
+
n
2
−
1
d
y
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
t
n
2
−
1
∫
0
+
∞
e
−
n
t
2
m
y
e
−
1
2
y
y
m
+
n
2
−
1
d
y
=
2
−
n
+
m
2
Γ
(
n
2
)
Γ
(
m
2
)
⋅
(
n
m
)
n
2
t
n
2
−
1
∫
0
+
∞
e
−
n
t
+
m
2
m
y
y
m
+
n
2
−
1
d
y
f(t)=\frac{dF(t)}{dt}=\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}\int_{0}^{+\infty}e^{-\frac{ny}{2m}t}e^{-\frac{1}{2}y}t^{\frac{n}{2}-1}y^{\frac{m+n}{2}-1}dy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}\int_{0}^{+\infty}e^{-\frac{nt}{2m}y}e^{-\frac{1}{2}y}y^{\frac{m+n}{2}-1}dy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}\int_{0}^{+\infty}e^{-\frac{nt+m}{2m}y}y^{\frac{m+n}{2}-1}dy
f(t)=dtdF(t)==Γ(2n)Γ(2m)2−2n+m⋅(mn)2n∫0+∞e−2mnyte−21yt2n−1y2m+n−1dy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1∫0+∞e−2mntye−21yy2m+n−1dy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1∫0+∞e−2mnt+myy2m+n−1dy
我们设 z = n t + m 2 m y , y = 2 m n t + m z z=\frac{nt+m}{2m}y,y=\frac{2m}{nt+m}z z=2mnt+my,y=nt+m2mz,那么 d y = 2 m n t + m d z dy=\frac{2m}{nt+m}dz dy=nt+m2mdz,从而得到以下的结果
f ( t ) = 2 − n + m 2 Γ ( n 2 ) Γ ( m 2 ) ⋅ ( n m ) n 2 t n 2 − 1 ∫ 0 + ∞ e − n t + m 2 m y y m + n 2 − 1 d y = 2 − n + m 2 Γ ( n 2 ) Γ ( m 2 ) ⋅ ( n m ) n 2 t n 2 − 1 ∫ 0 + ∞ e − z ( 2 m n t + m z ) m + n 2 − 1 2 m n t + m d z = 2 − n + m 2 Γ ( n 2 ) Γ ( m 2 ) ⋅ ( n m ) n 2 t n 2 − 1 ( 2 m n t + m ) m + n 2 ∫ 0 + ∞ e − z z m + n 2 − 1 d z = 2 − n + m 2 Γ ( n 2 ) Γ ( m 2 ) ⋅ ( n m ) n 2 t n 2 − 1 ( 2 m n t + m ) m + n 2 Γ ( m + n 2 ) = Γ ( m + n 2 ) Γ ( n 2 ) Γ ( m 2 ) ⋅ ( n m ) n 2 t n 2 − 1 ( n m t + 1 ) − m + n 2 f(t)=\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}\int_{0}^{+\infty}e^{-\frac{nt+m}{2m}y}y^{\frac{m+n}{2}-1}dy\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}\int_{0}^{+\infty}e^{-z}(\frac{2m}{nt+m}z)^{\frac{m+n}{2}-1}\frac{2m}{nt+m}dz\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}(\frac{2m}{nt+m})^{\frac{m+n}{2}}\int_{0}^{+\infty}e^{-z}z^{\frac{m+n}{2}-1}dz\\ =\frac{2^{-\frac{n+m}{2}}}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}(\frac{2m}{nt+m})^{\frac{m+n}{2}}\Gamma(\frac{m+n}{2})\\ =\frac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}\cdot{(\frac{n}{m})^{\frac{n}{2}}}t^{\frac{n}{2}-1}(\frac{n}{m}t+1)^{-\frac{m+n}{2}} f(t)=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1∫0+∞e−2mnt+myy2m+n−1dy=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1∫0+∞e−z(nt+m2mz)2m+n−1nt+m2mdz=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1(nt+m2m)2m+n∫0+∞e−zz2m+n−1dz=Γ(2n)Γ(2m)2−2n+m⋅(mn)2nt2n−1(nt+m2m)2m+nΓ(2m+n)=Γ(2n)Γ(2m)Γ(2m+n)⋅(mn)2nt2n−1(mnt+1)−2m+n
易知, Γ ( n 2 ) Γ ( m 2 ) Γ ( m + n 2 ) = B ( n 2 , m 2 ) \frac{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}{\Gamma(\frac{m+n}{2})}=\Beta(\frac{n}{2},\frac{m}{2}) Γ(2m+n)Γ(2n)Γ(2m)=B(2n,2m)
所以,最终求得 F F F分布的表达式为
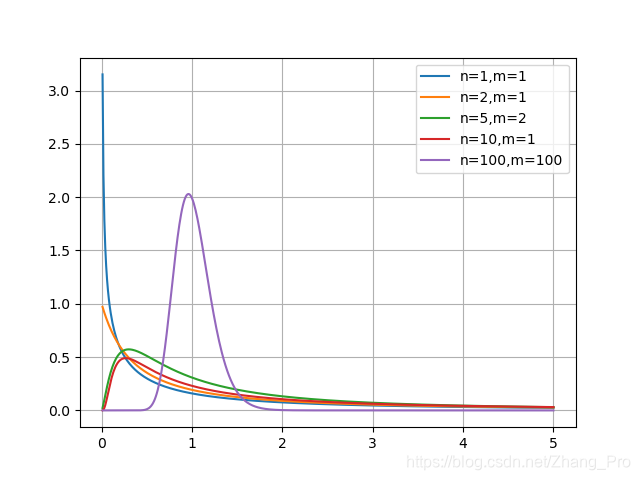
F ( x ∣ n , m ) = { ( n m ) n 2 B ( n 2 , m 2 ) x n 2 − 1 ( 1 + n m x ) − n + m 2 , if x ≥ 0 0 , if x < 0 F(x|n,m)=\begin{cases} \frac{(\frac{n}{m})^{\frac{n}{2}}}{B(\frac{n}{2},\frac{m}{2})}x^{\frac{n}{2}-1}(1+\frac{n}{m}x)^{-\frac{n+m}{2}}&,\text{ if }x\geq{0}\\ 0&,\text{ if }x<0 \end{cases} F(x∣n,m)={B(2n,2m)(mn)2nx2n−1(1+mnx)−2n+m0, if x≥0, if x<0
在 F F F分布中,其中的方差和均值为
E ( F ) = E ( m n ⋅ X Y ) = m n E ( X Y ) = m n E ( X ) E ( 1 Y ) = m n ⋅ n ⋅ 1 m − 2 = m m − 2 E(F)=E(\frac{m}{n}\cdot{\frac{X}{Y}})=\frac{m}{n}E(\frac{X}{Y})=\frac{m}{n}E(X)E(\frac{1}{Y})=\frac{m}{n}\cdot{n}\cdot{\frac{1}{m-2}}=\frac{m}{m-2} E(F)=E(nm⋅YX)=nmE(YX)=nmE(X)E(Y1)=nm⋅n⋅m−21=m−2m
var ( F ) = var ( m n ⋅ X Y ) = m 2 n 2 E ( X 2 Y 2 ) − ( E ( m n ⋅ X Y ) ) 2 \text{var}(F)=\text{var}(\frac{m}{n}\cdot{\frac{X}{Y}})\\ =\frac{m^{2}}{n^{2}}E(\frac{X^{2}}{Y^{2}})-(E(\frac{m}{n}\cdot{\frac{X}{Y}}))^{2} var(F)=var(nm⋅YX)=n2m2E(Y2X2)−(E(nm⋅YX))2
其中, E ( X 2 Y 2 ) = E ( X 2 ) E ( 1 Y 2 ) E(\frac{X^{2}}{Y^{2}})=E(X^{2})E(\frac{1}{Y^{2}}) E(Y2X2)=E(X2)E(Y21),那么可以知道
E ( X 2 ) = var ( X ) + ( E ( X ) ) 2 = 2 n + n 2 E(X^{2})=\text{var}(X)+(E(X))^{2}=2n+n^{2} E(X2)=var(X)+(E(X))2=2n+n2
E ( 1 Y 2 ) = 2 − m 2 Γ ( m 2 ) ∫ 0 + ∞ 1 x 2 e − 1 2 x x m 2 − 1 d x = 2 − m 2 Γ ( m 2 ) ∫ 0 + ∞ e − 1 2 x x m 2 − 3 d x E(\frac{1}{Y^{2}})=\frac{2^{-\frac{m}{2}}}{\Gamma(\frac{m}{2})}\int_{0}^{+\infty}\frac{1}{x^{2}}e^{-\frac{1}{2}x}x^{\frac{m}{2}-1}dx\\ =\frac{2^{-\frac{m}{2}}}{\Gamma(\frac{m}{2})}\int_{0}^{+\infty}e^{-\frac{1}{2}x}x^{\frac{m}{2}-3}dx E(Y21)=Γ(2m)2−2m∫0+∞x21e−21xx2m−1dx=Γ(2m)2−2m∫0+∞e−21xx2m−3dx
做变换 z = x 2 z=\frac{x}{2} z=2x,则 x = 2 z , d x = 2 d z x=2z,dx=2dz x=2z,dx=2dz,于是
E ( 1 Y 2 ) = 2 − m 2 Γ ( m 2 ) ∫ 0 + ∞ e − z ( 2 z ) m 2 − 3 2 d z = 1 4 Γ ( m 2 ) ∫ 0 + ∞ e − z z m 2 − 3 d z = 1 4 Γ ( m 2 ) ⋅ Γ ( m 2 − 2 ) E(\frac{1}{Y^{2}})=\frac{2^{-\frac{m}{2}}}{\Gamma(\frac{m}{2})}\int_{0}^{+\infty}e^{-z}(2z)^{\frac{m}{2}-3}2dz\\ =\frac{1}{4\Gamma(\frac{m}{2})}\int_{0}^{+\infty}e^{-z}z^{\frac{m}{2}-3}dz\\ =\frac{1}{4\Gamma(\frac{m}{2})}\cdot{\Gamma(\frac{m}{2}-2)} E(Y21)=Γ(2m)2−2m∫0+∞e−z(2z)2m−32dz=4Γ(2m)1∫0+∞e−zz2m−3dz=4Γ(2m)1⋅Γ(2m−2)
而
Γ
(
m
2
)
=
(
m
2
−
1
)
Γ
(
m
2
−
1
)
=
(
m
2
−
2
)
(
m
2
−
1
)
Γ
(
m
2
−
2
)
\Gamma(\frac{m}{2})=(\frac{m}{2}-1)\Gamma(\frac{m}{2}-1)=(\frac{m}{2}-2)(\frac{m}{2}-1)\Gamma(\frac{m}{2}-2)
Γ(2m)=(2m−1)Γ(2m−1)=(2m−2)(2m−1)Γ(2m−2)
即
Γ ( m 2 − 2 ) Γ ( m 2 ) = 4 ( m − 2 ) ( m − 4 ) \frac{\Gamma(\frac{m}{2}-2)}{\Gamma(\frac{m}{2})}=\frac{4}{(m-2)(m-4)} Γ(2m)Γ(2m−2)=(m−2)(m−4)4
所以
E ( 1 Y 2 ) = 1 ( m − 2 ) ( m − 4 ) E(\frac{1}{Y^{2}})=\frac{1}{(m-2)(m-4)} E(Y21)=(m−2)(m−4)1
故而
var
(
F
)
=
m
2
n
2
⋅
n
(
n
+
2
)
⋅
1
(
m
−
2
)
(
m
−
4
)
−
(
m
m
−
2
)
2
=
2
m
2
(
m
+
n
−
2
)
n
(
m
−
2
)
2
(
m
−
4
)
\text{var}(F)=\frac{m^{2}}{n^{2}}\cdot{n(n+2)}\cdot{\frac{1}{(m-2)(m-4)}}-(\frac{m}{m-2})^{2}=\frac{2m^{2}(m+n-2)}{n(m-2)^{2}(m-4)}
var(F)=n2m2⋅n(n+2)⋅(m−2)(m−4)1−(m−2m)2=n(m−2)2(m−4)2m2(m+n−2)
F分布的概率密度函数图像如下所示
3. 应用
这三大概率抽样分布
χ
2
\chi^{2}
χ2分布、t分布和F分布是最重要的分布函数。经过上面的证明和讨论,相信已经对这三种分布函数有了很深的理解。在机器学习和数据挖掘中,我们可以通过使用这三种概率模型对样本数据进行概率推断,然后对一些数据进行预测和模拟。
χ
2
\chi^{2}
χ2分布主要有两个用途:
- 用于检验拟合优良程度,检验一组数据与指定曲线的拟合程度,或者检验某组观察值是否符合某种分布情况。
- 检验两个变量的独立性,通过这个方法检查两个变量之间是否存在某种关联。
一般来说,通过检验统计量
X
2
=
∑
k
=
1
n
(
O
−
E
)
2
E
X^{2}=\sum\limits_{k=1}^{n}\frac{(O-E)^{2}}{E}
X2=k=1∑nE(O−E)2比较期望结果与实际结果的差别之处。
t分布和F分布主要应用于区间估计中。这是从点估计值和抽样标准误差同时出发的,是先给定概率值,然后再简历的包含待估计参数的区间,其中这个给定的概率值被称作置信度或者是置信水平。在参数估计中,对总体进行区间估计的时候,通常考虑到总体是否为正态分布、总方差是否为已知、又或用于构造统计量的样本是否为正态分布等等情况。
小结
本小节介绍了 χ 2 \chi^{2} χ2分布、t分布以及F分布,这些分布在一些概率推断,尤其是变分推断和贝叶斯推断中有着举足轻重的作用。在接下来的博文中,笔者会介绍一些关于这些概率分布函数的推断以及在程序中的应用等。