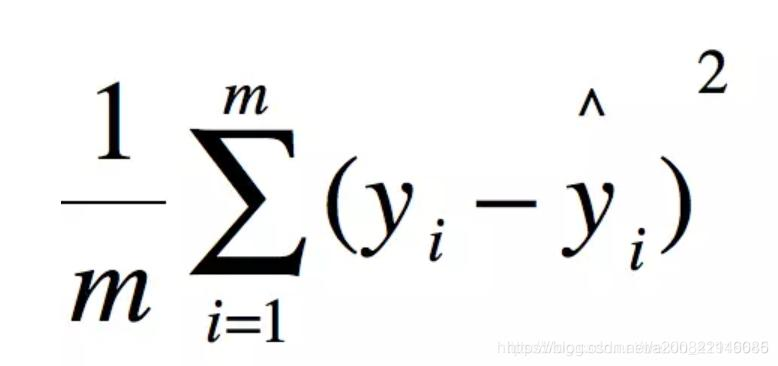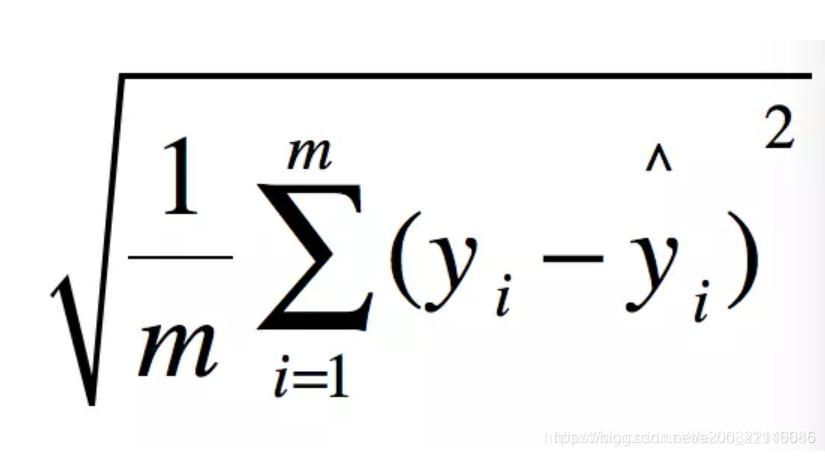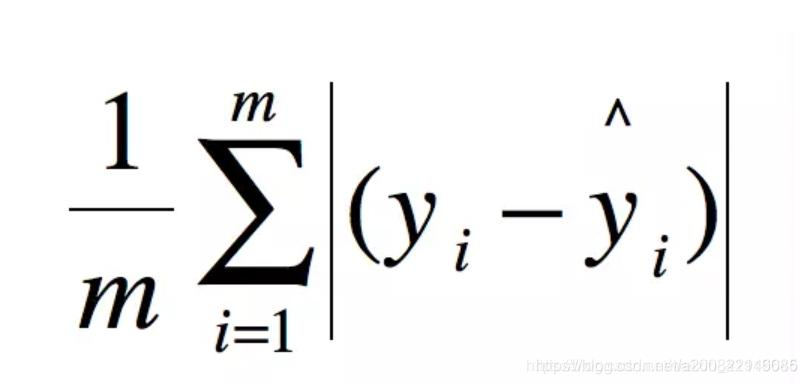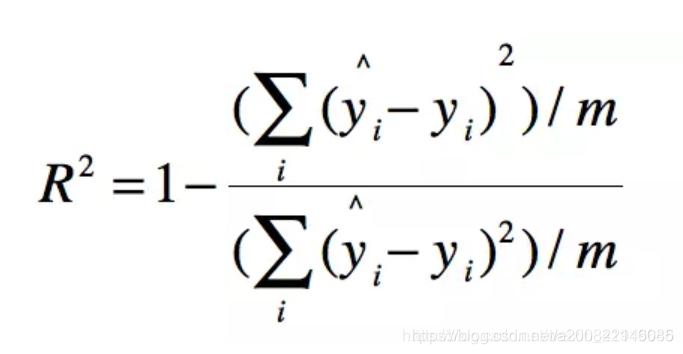一、MSE 均方误差
即(真实值-预测值)的平方/测试集个数
其实(真实值-预测值)的平方 就是线性回归的损失函数,线性回归的目的就是为了让损失函数最小化。但这种判断方式是会放大误差的,即本身误差越大的平方后会更大。所以从这也可以看出,损失函数是为了减小最大的那个误差。
二、RMSE 均方根误差
即MSE开根号,使结果的单位和数据集一致,更好描述
三、MAE 平均绝对误差
四、R-Squared
以上3种评价方式,针对不同的模型,有不同的单位。比如米,元。这些不同的单位缺乏可读性。
衡量分类算法通常使用准确率进行衡量,那么衡量回归算法就引入了R-Squared
化简上面公式
分子就变成了我们的均方误差MSE,下面分母就变成了方差。
这里的基准模型即取平均值。分式的分母为方差公式,若R**2<0,即分子大于分母,预测模型误差大于基准模型。
五、实现代码
#这里我们使用sklearn数据集中的波士顿房产数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datastes
boston=datasets.load_boston()
x=boston.data[:,5]
y=boston.target
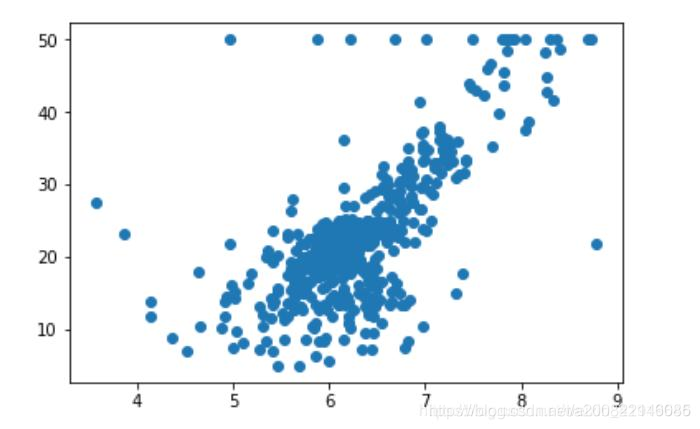
plt.scatter(x,y)
plt.show()
#这里看出y=50的一行数据比较奇怪,因为可能设置了一个上限,所有大于50的y都设置成了50,我们不取这部分值
x=x[y<50.0]
y=y[y<50.0]
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
x_train=np.array(x_train).reshape(-1,1)#因为我们只对一个特征进行预测,改变成数组形式
reg.fit(x_train,y_train)
reg.coef_ #即a
reg.intercept_ #即b 截距
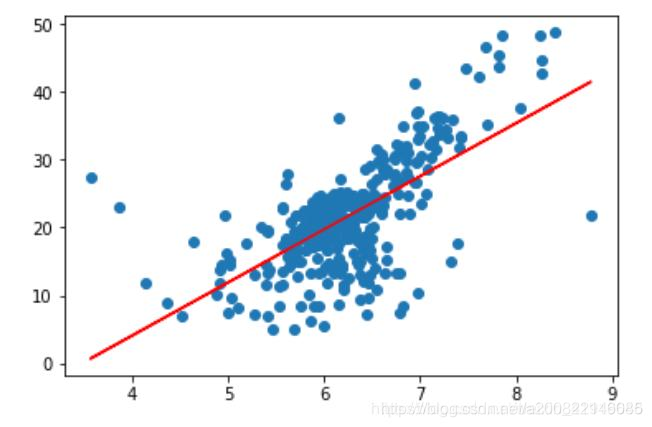
#进行可视化
plt.scatter(x_train,y_train)
plt.plot(x_train,reg.predict(x_train),color='r')
plt.show()
x_test=np.array(x_test).reshape(-1,1)
y_predict=reg.predict(x_test)
#MSE 均方误差
mse_test=np.sum(y_test-y_predict)**2/len(y_test)
#RMSE 均方根
from math import sqrt
rmse_test=sqrt(mse_test)
#MAE 平均绝对误差
mae_test=np.sum(np.absolute(y_test-y_predict))/len(y_test)
#R-Square
R_test=1-mse_
test/np.var(y_test)
#使用sklearn中的方法
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
#MSE
mean_squared_error(y_test,y_predict)
#MAE
mean_absolute_error(y_test,y_predict)
#R-Square
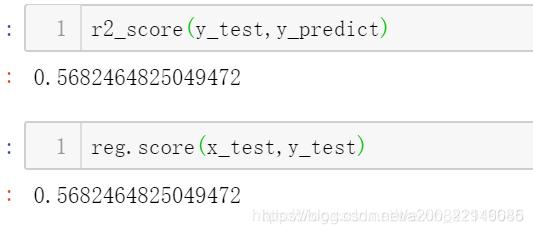
r2_score(y_test,y_predict)
#线性回归中采用的评分标准就是R-Square
reg.score(x_test,y_test)