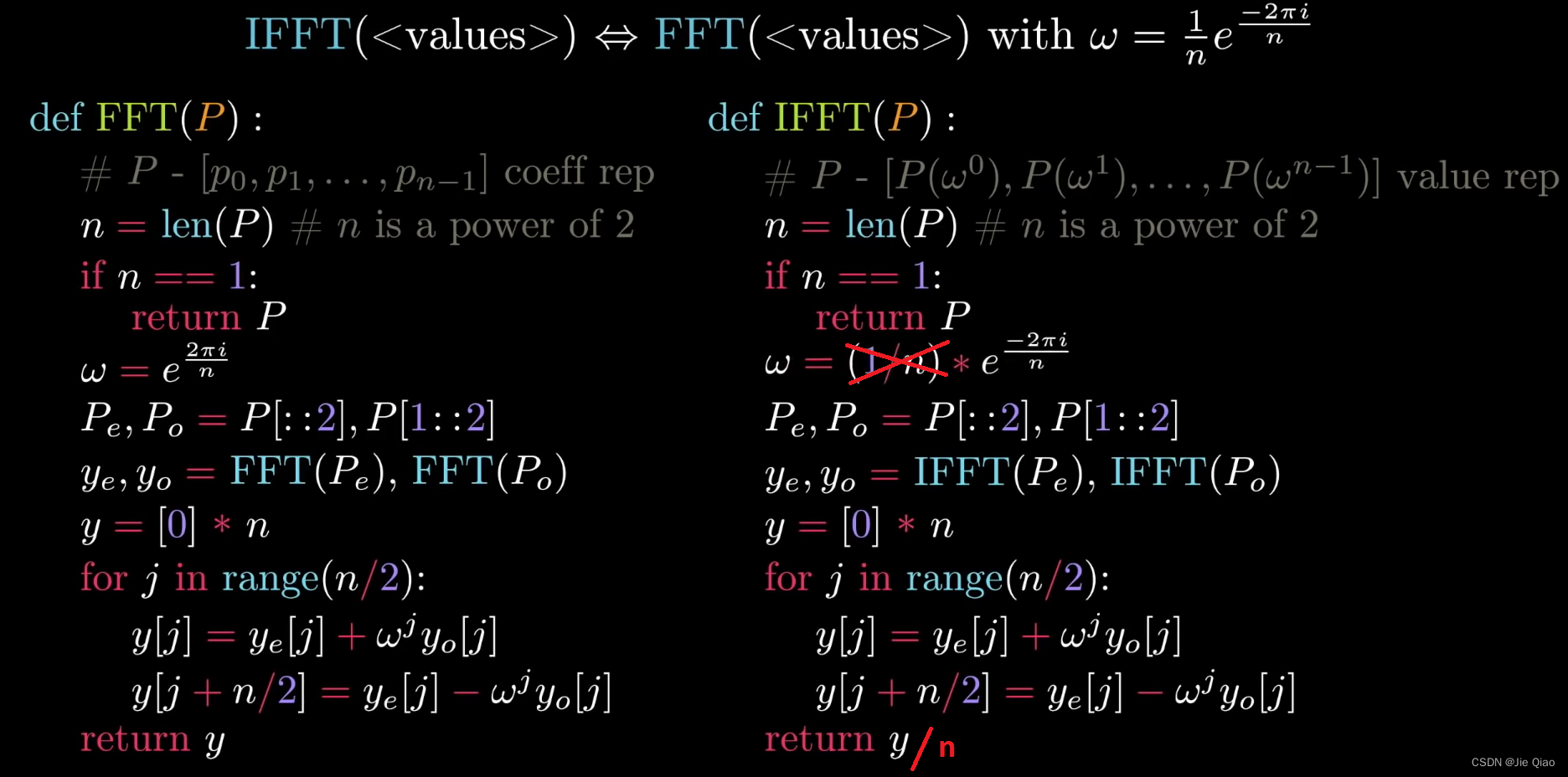本文是视频The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?的整理。

离散傅里叶变换的用法

FFT是一个非常快速的离散傅里叶变换算法，他的算法复杂度是$O(n\log n)$。在讲解FFT之前，我们先介绍普通的离散傅里叶变换的的输入和输出是什么？以及一个离散傅里叶变换的简单应用。离散傅里叶变换的输入是一个数组，比如[5,3,2,1]，输出是对应的复数，[11,3-2i,3,3+2i]，可以自己试试：

from numpy.fft import fft
fft([5,3,2,1])

这个5,3,2,1可以看做是一个多项式的系数：

$$P(x)=5+3x+2x^2+x^3$$

而这个对应的复数其实是这个多项式的在点$P\left(w^0\right),P\left(w^1\right),P\left(w^2\right),P\left(w^3\right)$的值，其中$w=e^{2\pi i/n}$,这里$n=4$。之所以$w$要设置成这个值是因为复数有个神奇的周期性：

对应着，$w^0=1,w^1=e^{2\pi i/4}=i,w^2=e^{4\pi i/4}=-1,w^3=e^{6\pi i/4}=-i$，可以发现他相当于从1开始，在这个单位元上平均取了4个点，而且这4个点正是多项式$x^4=1$的根。可以看下面这个视频，里面也介绍了复数的这种周期性的性质：

【官方双语】奥数级别的数数问题

我们把这四个点代进方程

$$\begin{array}{rl}P\left(w^0\right)& =5+3+2+1=P(1)=11\\ P\left(w^1\right)& =5+3\omega +2{\omega }^2+{\omega }^3=P(i)=3+2i\\ P\left(w^2\right)& =5+3{\omega }^2+2{\omega }^4+{\omega }^6=P(-1)=3\\ P\left(w^3\right)& =5+3{\omega }^3+2{\omega }^6+{\omega }^9=P(-i)=3-2i\end{array}$$

写成矩阵的形式就是：
$$\left[\begin{array}{c}P\left({\omega }^0\right)\\ P\left({\omega }^1\right)\\ P\left({\omega }^2\right)\\ P\left({\omega }^3\right)\end{array}\right]=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& \omega & {\omega }^2& {\omega }^3\\ 1& {\omega }^2& {\omega }^4& {\omega }^6\\ 1& {\omega }^3& {\omega }^6& {\omega }^9\end{array}\right]\left[\begin{array}{c}5\\ 3\\ 2\\ 1\end{array}\right]\text{\hspace{1em}(1)}$$
那这个傅里叶变换有什么用呢？以下以多项式相乘为例子

多项式相乘

如果我们想知道两个多项式相乘会变成怎样：

$$\begin{array}{rl}Q(x)& =P(x)\ast P(x)\\ & =\left(5+3x+2x^2+x^3\right)\left(5+3x+2x^2+x^3\right)\\ & =x^6+4x^5+10x^4+22x^3+29x^2+30x+25\end{array}$$

显然，要计算这个新的Q，我们需要每个系数对应相乘，其时间复杂度应该是$O\left(n^2\right)$，那有没有更加快速的方法呢？

多项式可以用点来表示

先介绍多项式的一个重要性质，那就是可以用若干个取值点来唯一表示这个多项式，比如一条线可以用两个点来表示表示：

类似的，对于d阶多项式，可以用d+1个点唯一表示（复数的点也是可以的）

注意到，我们刚才说过，[5,3,2,1]的他的傅里叶变换其实对应着多项式的4个点的取值！所以如果我们想知道$Q$的形式，那么我们就需要知道7个点，而如果我们能够找到$P(x)$的7个不同取值，那么我们就能非常轻易的得到$Q(x)$的7个取值:

$$\begin{gathered} Q\left({\omega }^0\right)=P\left({\omega }^0\right)P\left({\omega }^0\right) \\ ... \\ Q\left({\omega }^6\right)=P\left({\omega }^6\right)P\left({\omega }^6\right) \end{gathered}$$

而为了找到这7个取值，我们可以对数组[5,3,2,1,0,0,0]做FFT，就可以轻易的找到对应的7个取值！即得到$\left[P\left({\omega }^0\right),...,P\left({\omega }^6\right)\right]$,将其对应相乘就可以得到$\left[Q\left({\omega }^0\right),...,Q\left({\omega }^6\right)\right]$了，现在如果我们能够将$Q$转回系数，那么我们就成功还原出Q了！将公式(1)扩展到任意维度，离散傅里叶变换可以用这样的矩阵乘法表示：
$$\left[\begin{array}{c}Q\left({\omega }^0\right)\\ Q\left({\omega }^1\right)\\ Q\left({\omega }^2\right)\\ ⋮\\ Q\left({\omega }^{n-1}\right)\end{array}\right]=\underset{\text{Discrete Fourier Transform }(\mathrm{DFT})\text{ matrix }}{\underbrace{\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& \omega & {\omega }^2& \cdots & {\omega }^{n-1}\\ 1& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{n-1}& {\omega }^{2(n-1)}& \cdots & {\omega }^{(n-1)(n-1)}\end{array}\right]}}\left[\begin{array}{c}{p}_0\\ p_1\\ p_2\\ ⋮\\ p_{n-1}\end{array}\right]\text{\hspace{1em}(2)}$$
这意味着只要我们可以求出矩阵的逆，就能反推出这个Q的系数了！而这个矩阵的逆的形式其实很简单：

$${\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& \omega & {\omega }^2& \cdots & {\omega }^{n-1}\\ 1& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{n-1}& {\omega }^{2(n-1)}& \cdots & {\omega }^{(n-1)(n-1)}\end{array}\right]}^{-1}=\frac{1}{n}\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }^{-1}& {\omega }^{-2}& \cdots & {\omega }^{-(n-1)}\\ 1& {\omega }^{-2}& {\omega }^{-4}& \cdots & {\omega }^{-2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{-(n-1)}& {\omega }^{-2(n-1)}& \cdots & {\omega }^{-(n-1)(n-1)}\end{array}\right]$$

这意味着什么？还记得我们FFT是干嘛的吗？那就是从$[p_0,...,p_{n-1}]$以$O(n\log n)$的速度变出$P\left(w^0\right),...,P\left(w^{n-1}\right)$，按照这两个矩阵非常相似的形式，我们或许可以再利用FFT算法，将$P\left(w^0\right),...,P\left(w^{n-1}\right)$快速地变回$[p_0,...,p_{n-1}]$. 而这正是快速傅里叶逆变换！通过这一通操作，我们发现原本的时间复杂度已经从$O\left(n^2\right)$降成了$O(n\log n)$！

FFT原理

那FFT到底是怎么快速的找到$P\left(w^0\right),...,P\left(w^{n-1}\right)$这n个不同点的取值的呢？显然如果是直接按照公式(2)进行矩阵计算这个复杂度其实还是平方级的。那FFT到底是怎么将这个时间缩减的呢？

答案是利用函数的对称性！比如对于$P(x)=x^2$，如果我们知道$P(1)=1$，根据偶函数的性质就有$P(-1)=P(1)=1$，于是，我们就只需要计算$n/2$个点的取值而不需要每一个取值都去计算！这个思想能不能推广到任意的多项式分布去呢？

对于任意的一个多项式函数，我们都能分解成偶函数和奇函数两项：

$$\begin{gathered} P(x)=3x^5+2x^4+x^3+7x^2+5x+1 \\ P(x)=\underset{P_e\left(x^2\right)}{\underbrace{\left(2x^4+7x^2+1\right)}}+\underset{P_o\left(x^2\right)}{\underbrace{\left(3x^4+x^2+5\right)}} \end{gathered}$$

从而有
$$\begin{gathered} P(x)=P_e\left(x^2\right)+x{P}_o\left(x^2\right) \\ P(-x)=P_e\left(x^2\right)-x{P}_o\left(x^2\right)\text{\hspace{1em}(3)} \end{gathered}$$
有了这个等式，我们似乎可以构造一种递归的算法，因为每一个$P$都可以分解为两项，而每一项又只需要计算$n/2$次，不停的递归下去就能最终得到$O(n\log n)$的计算复杂度。然而问题是，如果我们的x是实数，这个递归是无法进行下去的，因为里面$x^2$永远是正的，这个递归就不成立。

而这正是我们使用复数的原因，还记得，我们$w$是一个具有周期性复数，我们可以发现，以4个取值为例：

可以发现，$w^0=-w^2$，$w^1=-w^3$, 这时候，即使是平方，我们也能找到对应的负数，从而，我们只需要算出$P\left(w^0\right)$和$P\left(w^1\right)$就能根据公式(3)轻易推出其对应的$P(w^3)$和$P(w^2)$：

$$\begin{gathered} P(w^1)=P_e\left({\left(w^1\right)}^2\right)+w^1{P}_o\left({\left(w^1\right)}^2\right)=P_e\left(w^2\right)+w^1{P}_o\left(w^2\right) \\ P(-w^1)=P_e\left({\left(w^1\right)}^2\right)-w^1{P}_o\left({\left(w^1\right)}^2\right)=P_e\left(w^2\right)-w^1{P}_o\left(w^2\right)=P(w^3) \end{gathered}$$

可以看到，我们只需要计算出$P_e\left(w^2\right)和P_o\left(w^2\right)$，就能用这个结果计算出$P(w^3)$. 而且计算$P_e\left(w^2\right)和P_o\left(w^2\right)$这两个数又可以递归的进行，这就是FFT算法的原理了，他正式巧妙的利用了复数的对称性质来找到一对对互为相反数的多项式取值，从而不需要去遍历所有的x。

FFT和IFFT的伪代码如下所示：

PS：原视频有个错误，这里改正了。
该算法其实就是不断递归的过程，而每一次递归我们又只需要n/2的计算量，从而快速求解离散傅里叶变换。另外逆变换也同样可以使用这个算法，只需要将w的值变一下就可以了。

总结

这篇文章介绍了，离散傅里叶变换其实是多项式到点表示的一种转换，而快速傅里叶变换则是发现，一些点的取值其实可以由其他的点得出，从而构造了一种快速的离散傅里叶计算方法。

参考资料

The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?

FFT Example: Unraveling the Recursion