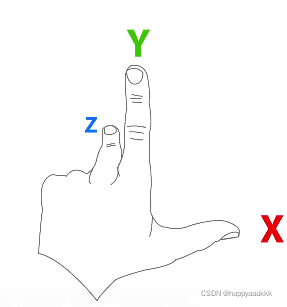
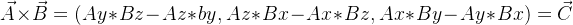Unity使用左手坐标系：拇指X轴，食指Y轴，中指Z轴。

计算公式：

设 A(Ax，Ay，Az)  B(Bx，By，Bz)，则

1.向量的模：

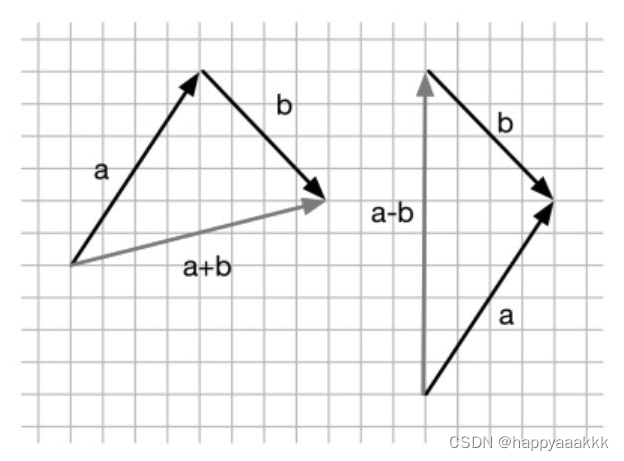
2.向量加法：

3.向量点积：

4.向量叉积：

物理（几何）意义：

1.模：就是向量的长度。

2.加减：是位移，遵循三角形法则。

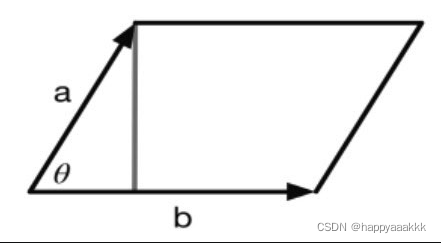
3.点积：结果是一个标量（数值，有大小无方向），满足交换律。

是一条边向另一条边的投影乘以另一条边的长度。

点积为0则两向量垂直，大于0是锐角（越大角度越小），小于0是钝角（越小角度越大）。

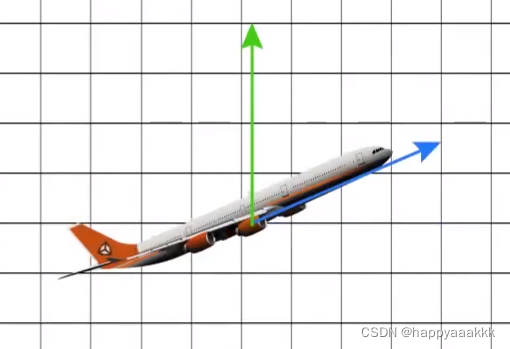
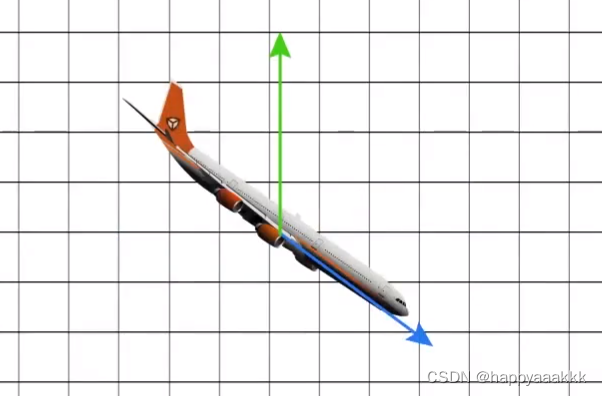
点乘结果描述了两个向量的“相似”程度，点乘结果越大，两向量越相近。

因为a•b = |a||b|cosθ

所以如果a和b都是单位向量，那么点乘的结果就是其夹角的cos值。

a•b = cosθ

由于cos在0~π上单调调减，因此可以比较cos值来达到比较夹角的效果。

4.叉积：结果是一个新的向量。

原向量是大拇指X和食指Y，新向量是中指Z（左手）。

叉积不满足交换律，即a×b≠b×a。实际上，叉积是满足反交换律的，即a×b=-(b×a)。而且叉积也不满足结合律，即 (a×b) ×c≠a×(b×c)

|a×b|=|a||b|sinθ，这和平行四边形的面积计算公式是一样的：

在Unity中：

1.计算向量的模：Vector3.magnitude

2.计算向量点积：Vector3.Dot(VectorA, VectorB)

3.计算向量叉积：Vector3.Cross(VectorA, VectorB)